Irrationaaliset numerot historia, ominaisuudet, luokittelu, esimerkit

Se irrationaaliset numerot He ovat niitä, joiden desimaalilmentäminen on äärettömiä lukuja ilman toistuvaa mallia, joten niitä ei voida saada tekemällä osamäärä minkä tahansa kahden kokonaisluvun välillä.

Tunnetuimpia irrationaalisia lukuja ovat:

Kuvio 1. Seuraavat irrationaaliset numerot ylhäältä alas: PI, Eulerin, Aúrean ja kahden neliöjuuren lukumäärä. Lähde: Pixabay.

Heidän joukossaan, epäilemättä π (PI) on tutuin, mutta niitä on paljon enemmän. Kaikki ne kuuluvat reaalilukujoukkoon, joka on numeerinen joukko, joka yhdistää rationaaliset ja irrationaaliset numerot.

Kuvan 1 keskeiset kohdat osoittavat, että desimaalit seuraavat määräämättömäksi ajaksi, tapahtuu, että nykyisten laskimen tila sallii vain muutaman näyttää.

Jos katsomme huolellisesti, jos teemme osamäärän kahden kokonaisluvun välillä, saadaan rajoitetut lukuja desimaalilla, jos ei, äärettömillä lukuilla, joissa yksi tai useampi ne toistetaan. No, tätä ei tapahdu irrationaalisilla numeroilla.

[TOC]

Irrationaalisten lukujen historia

Antiikin pythagoras -matemaatikko, syntynyt vuonna 582.C Samosissa, Kreikka, perusti Pythagoran ajattelun ja löysi hänen nimensä kuuluisan lauseen. Meillä on se vasemmalle (babylonialaiset tunsivat hänet jo kauan ennen).

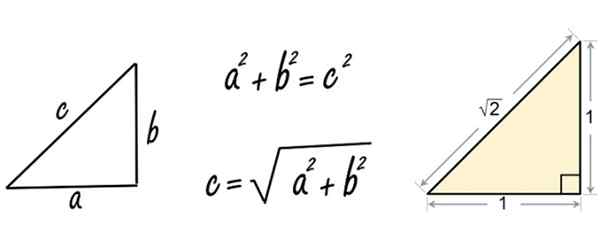Kuva 2. Pythagoras -lause, jota levitetään sivujen kolmioon, joka on yhtä suuri kuin 1. Lähde: Pixabay/Wikimedia Commons.

No, kun Pythagoras (tai luultavasti hänen opetuslapsi) sovelsi lauseen oikeanpuoleiseen kolmioon, joka oli yhtä suuri kuin 1, löysi irrationaalisen numeron √2.

Se voi palvella sinua: kuivausviivat

Hän teki sen tällä tavalla:

C = √1² + 1² = √1+1 = √2

Ja hän tajusi heti, että tämä uusi numero ei tullut kahden muun luonnollisen numeron välillä, jotka olivat tuolloin tiedossa.

Siksi hän kutsui häntä irrationaalinen, Ja löytö aiheutti suurta ahdistusta ja sekaannusta pythagorien keskuudessa.

Irrationaalisten lukujen ominaisuudet

-Kaikkien irrationaalisten numeroiden joukko on merkitty kirjaimella I ja joskus Q* tai Q^C. Irrationaalisten lukujen I tai Q* välinen liitto Q: n välinen osake.

-Irrationaalisten lukujen kanssa voidaan suorittaa tunnettuja aritmeettisia operaatioita: summa, vähennys, kertolasku, jakautuminen, potentiaatio ja paljon muuta.

-Jakoa 0 välillä ei ole määritelty irrationaalisten lukujen keskuudessa.

-Irrationaalisten lukujen välinen summa ja tuote ei välttämättä ole toinen irrationaalinen luku. Esimerkiksi:

√2 x √8 = √16 = 4

Ja 4 ei ole irrationaalinen luku.

-Rationaalisen lukumäärän ja irrationaalisen määrän summa johtaa kuitenkin irrationaaliseen. Tällä tavalla:

1 + √2 = 2.41421356237…

-Irrationaalisella numerolla on myös erilainen rationaalinen luku 0: sta Irrationaalisesti. Katsotaanpa tätä esimerkkiä:

2 x √2 = 2.828427125…

-Irrationaalisen käänteinen johtaa toiseen irrationaaliseen lukumäärään. Kokeilemme joitain:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Nämä luvut ovat mielenkiintoisia, koska ne ovat myös tiedossa olevien kulmien trigonometristen syiden arvoja. Suuri osa trigonometrisistä syistä on irrationaalisia lukuja, mutta on poikkeuksia, kuten Sen 30º = 0.5 = ½, joka on rationaalinen.

-Summuttomaiset ja assosiatiiviset ominaisuudet täyttyvät. Jos A ja B ovat kaksi irrationaalista numeroa, tämä tarkoittaa sitä:

Voi palvella sinua: Overjektiivitoiminto: Määritelmä, ominaisuudet, esimerkit

A + B = B + A.

Ja jos C on toinen irrationaalinen numero, niin:

(A + b) + c = a + (b + c).

-Kertolaskujen jakautuva ominaisuus summan suhteen on toinen tunnettu ominaisuus, joka on myös irrationaalisten lukujen kohdalla. Tässä tapauksessa:

-lla.(b+c) = a.b + a.c.

-Irrationaalinen on päinvastainen: -a. Kun tulos lisätään, se on 0:

A+(-a) = 0

-Kahden erilaisen rationaalisen välillä on ainakin yksi irrationaalinen luku.

Irrationaalisen numeron sijainti oikealla linjalla

Oikea viiva on vaakasuora viiva, jossa todelliset luvut sijaitsevat, joista irrationaaliset ovat tärkeä osa.

Löydämme irrationaalisen numeron oikealta linjalta, geometrisestä muodosta, voimme olla Pythagoras -lauseen, säännön ja kompassin arvoisia.

Esimerkiksi aiomme paikantaa √5 oikealle viivalle, jolle piirrämme suorakulmion kolmion sivusta x = 2 ja y = 1, Kuten kuva näyttää:

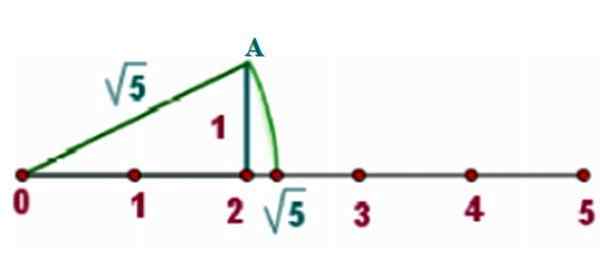Kuva 3. Menetelmä irrationaalisen numeron löytämiseksi oikealla linjalla. Lähde: f. Zapata.

Pythagoras -lauseessa tällaisen kolmion hypotenuse on:

C = √2² + 1² = √4+1 = √5

Nyt kärjellä oleva lyönti asetetaan 0: een, missä on myös yksi oikean kolmion kärkipisteistä. Kompassikynän kärjen on oltava kärjen kohdalla.

Piirretään kehäkaari, joka leikkaa todellisen viivan. Koska etäisyys ympäryskeskuksen ja minkä tahansa saman pisteen välillä on säde, joka on √5: n arvoinen, risteyspiste on myös √5 keskustasta.

Kaaviosta nähdään, että √5 on välillä 2 ja 2.5. Laskin tarjoaa meille likimääräisen arvon:

Voi palvella sinua: Määrityskerroin: kaavat, laskenta, tulkinta, esimerkkejä

√5 = 2.236068

Ja niin, rakentaa kolmio sopivien puolten kanssa, muut irrationaaliset puolet, kuten √7 ja muut.

Irrationaalisten lukujen luokittelu

Irrationaaliset numerot luokitellaan kahteen ryhmään:

-Algebrallinen

-Transsendentti tai transsendenttinen

Algebralliset numerot

Algebralliset numerot, jotka voivat olla irrationaalisia tai ei, ovat polynomiyhtälöiden ratkaisuja, joiden yleinen muoto on:

-lla_n xⁿ + -lla_N-1x^N-1 + -lla_N-2x^N-2 +.. . +-lla₁x + a_jompikumpi = 0

Esimerkki polynomiyhtälöstä on toisen asteen yhtälö tällainen:

x³ - 2x = 0

On helppo osoittaa, että irrationaalinen luku √2 on yksi tämän yhtälön ratkaisuista.

Transcendent numerot

Sen sijaan transsendenttiset luvut, vaikka irrationaaliset, eivät koskaan syntyvät polynomiyhtälön liuoksena.

Sovelletussa matematiikassa yleisimmin esiintyneet transcendenttiset numerot ovat π, niiden suhteisiin kehä ja lukumäärä E tai euler -numero, joka on Neperian logaritmien perusta.

Harjoittele

Mustalla neliöllä harmaa asetetaan kuvaan ilmoitettuun asentoon. On tiedossa, että mustan neliön pinta on 64 cm². Kuinka paljon molempien neliöiden pituudet ovat?

Kuva 4. Kaksi neliötä, joista sivujen pituus löytyy. Lähde: f. Zapata.

Vastaus

Sivu L -neliön pinta on:

A = l²

Koska musta neliö on 64 cm² alueen, sen sivun on oltava 8 cm.

Tämä toimenpide on sama kuin Diagonaali harmaa neliö. Pythagoras -lauseen soveltaminen tähän diagonaaliin ja muistamalla, että neliön sivut mittaavat samalla tavalla: meillä on:

8² = L_g² + Lens_g²

Missä l_g Se on harmaan neliön puoli.

Siksi: 2L_g² = 8²

Neliöjuuren soveltaminen tasa -arvon molemmille puolille:

Lens_g = (8/√2) cm

Viitteet

1. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
2. Figuera, J. 2000. 9. matematiikka. Aste. Co-bo-painikkeet.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Koulutusportaali. Irrationaaliset numerot ja niiden ominaisuudet. Haettu: Portaledukatiivi.netto.
5. Wikipedia. Irrationaaliset numerot. Palautettu: on.Wikipedia.org.