Täydelliset numerot kuinka tunnistaa ne ja esimerkkejä

Eräs Täydellinen numero on luonnollinen numero siten, että Sen jakajien summa on sama kuin luku. Ilmeisesti sitä ei voida sisällyttää jakajien joukkoon itse lukuun.

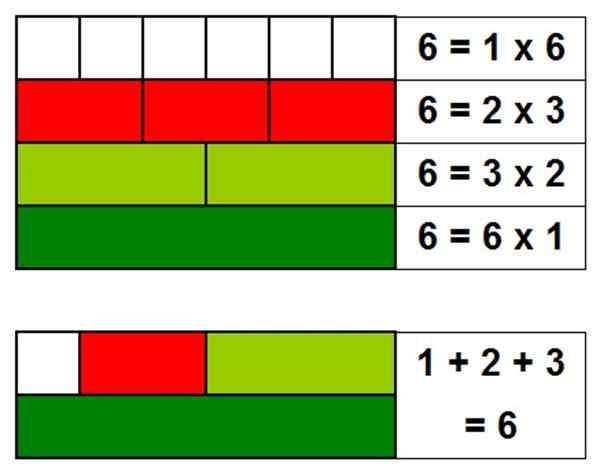
Yksi yksinkertaisimmista esimerkeistä täydellisestä määrästä on 6, koska sen jakajat ovat: 1, 2 ja 3. Jos lisäämme jakajat, se saadaan: 1 + 2 + 3 = 6.

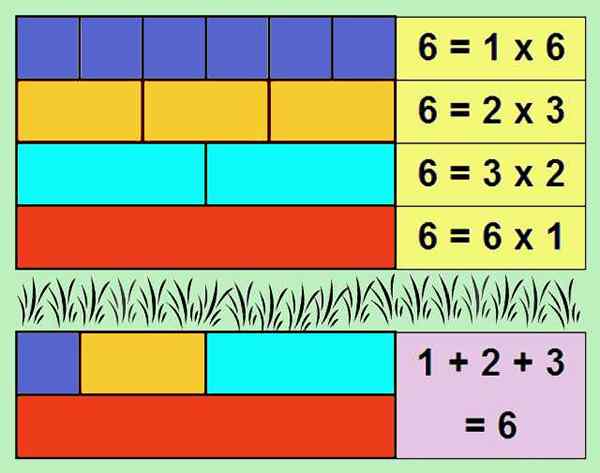Kuvio 1. Numero 6 on täydellinen, koska sen jakajien summa, lukuun ottamatta itse numeroa, antaa numeron 6. Lähde: Itse tehty

Kokonaislukujen jakajien summaa, lukuun ottamatta itseään, kutsutaan alikvootti. Siksi täydellinen luku on yhtä suuri kuin sen alikvootti.

Mutta jos lukumäärän jakautumisten summa, jonka numero itsessään on, niin täydellinen luku on yksi, että kaikkien sen jakajien summa 2: lla on yhtä suuri kuin itse luku.

[TOC]

Historia

Antiikin matemaatikot, erityisesti kreikkalaiset, antoivat suuren merkityksen täydellisille määrille ja omistautuneille jumalallisille ominaisuuksille.

Esimerkiksi Philo de Alejandría väitti, että 6 ja 28 väittivät, että 6 ja 28 ovat täydellisiä lukuja, jotka vastaavat maailman luomisen kuuden päivän ja kaksikymmentäkymmenennenkymmenen päivän päivää, jotka Kuu kääntyy ympäri maata.

Täydelliset numerot ovat myös luonteeltaan, esimerkiksi Saturnuksen pohjoisnavalla näyttää myös täydelliseltä numerolta 6, kuusikulmaisen muotoisen pyörteen, jonka Cassini -koetin on löytänyt ja joka on kiinnostunut tutkijoille. 

Mehiläishunajakennoilla on solut kuusikulmaisessa muodossa, toisin sanoen 6 puolella.  On osoitettu, että monikulmio, jolla on täydellinen numero 6.

Kuva 2. Täydellinen numero 6 on läsnä mehiläisissä hunajakennoissa. On osoitettu, että tällä sivuilla solujen muodostamiseen käytettävän vahan määrä on minimaalinen. Lähde: Pixabay.

Täydelliset numerot ominaisuudet

Kaikkien luonnollisen luvun n jakajien summa on merkitty σ (n): lla. Täydellisessä numerossa on totta, että: σ (n) = 2n.

Euclid -kaava ja kriteerit

Euclid löysi kaavan ja kriteerin, jonka avulla voit löytää täydelliset numerot. Tämä kaava on:

2^(N-1) (2ⁿ -1)

Kaavan tuottama lukumäärä on kuitenkin täydellinen vain kun tekijä (2ⁿ -1) Ole serkku.

Voi palvella sinua: vektorin suorakulmaiset komponentit (harjoituksilla)

Katsotaanpa kuinka ensimmäiset täydelliset numerot luodaan:

Jos n = 2, meillä on 2¹ (2² - 1) = 2 x 3 = 6, jonka näimme jo täydellisen.

Kun n = 3 sinulla on 2² (2³ - 1) = 4 x 7 = 28, joka on myös täydellinen, koska se varmistetaan yksityiskohtaisesti esimerkissä 1.

Katsotaanpa mitä tapahtuu n = 4. Korvaamalla euklidikaava, meillä on:

2³ (2⁴ - 1) = 8 x 15 = 120

Voidaan varmistaa, että tämä numero ei ole täydellinen, kuten esimerkissä 3 esitetään yksityiskohtaisesti. Tämä ei ole ristiriidassa euklidikriteerien kanssa, koska 15 ei ole serkku, välttämätön vaatimus tuloksen täydelliseksi lukumääräksi.

Katsotaanpa mitä tapahtuu, kun n = 5. Soveltamalla kaavaa:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Koska 31 on ensisijainen luku, joten numeron 496 on oltava täydellinen, euklidikriteerien mukaan. Esimerkissä 4 esitetään yksityiskohtaisesti, että se on käytännössä.

Alkeisluvut, joilla on lomake 2^p - 1 Heitä kutsutaan Mersennen serkuksille munkki Marin Mersennen kunniaksi, joka tutki päälukuja ja täydellisiä lukuja seitsemännentoista vuosisadan aikana.

Myöhemmin 1800 -luvulla Leonhard Euler osoitti, että kaikki Euclid -kaavan tuottamat täydelliset määrät ovat pareja.

Tähän mennessä on löydetty täydellinen, joka on outoa.

Suurin täydellinen numero tunnetaan

Nykyiseen päivämäärään 51 täydelliset numerot tunnetaan, kaikki muodostuvat kaava- ja euklidikriteerit. Tämä luku saatiin, kun Mersennen serkku löydettiin, mikä on: (2^82589933 - 1).

Täydellinen numero #51 on (2^82589933) X (2^82589933 - 1) ja siinä on 49724095 digitosta.

Täydellinen joukko on itsesi ystävä

Numeroteoriassa sanotaan, että kaksi numeroa ovat ystäviä, kun yhden jakajien summa, lukuun ottamatta itse lukua, on yhtä suuri kuin toinen luku ja päinvastoin.

Se voi palvella sinua: Line- ja Semi -River -segmentti

Lukija voi varmistaa, että 220: n jakajien summa, lukuun ottamatta 220 on 284. Toisaalta 284: n jakajien summa, lukuun ottamatta 284, on yhtä suuri kuin 220. Siksi numerot 220 ja 284 ovat ystäviä.

Tästä näkökulmasta täydellinen joukko on itsesi ystävä.

Esimerkkejä täydellisistä numeroista

Seuraavaksi luetellaan kahdeksan ensimmäistä täydellistä numeroa:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Harjoitukset

Seuraavissa harjoituksissa on tarpeen laskea numeron jakajat ja tehdä sitten summa ja tarkistaa, onko numero täydellinen luku vai ei.

Siksi ennen kuin käsittelemme harjoituksia, tarkistamme käsitteen ja osoitamme, kuinka ne lasketaan.

Aluksi sinun on muistettava, että numerot voivat olla serkkuja (kun ne voidaan jakaa vain tarkkaan itsensä ja 1: n kanssa) tai yhdisteisiin (kun ne voivat hajottaa ensisijaisten lukujen tuotteena).

Yhdistelmänumero n sinulla on:

N = aⁿ . b -^m. c^p … R^{k -k -} 

Missä a, b, c ... r ovat ensisijaisia ​​lukuja ja n, m, p ... k ovat luonnollisiin lukuihin kuuluvia eksponentteja, jotka voivat olla arvoltaan 1 eteenpäin.

Näiden eksponenttien suhteen on kaava tietää, kuinka monta jakajaa numero n on, vaikka se ei kerro meille, mitä nämä ovat. Olkoon c tämä määrä, sitten:

C = (n +1) (m +1) (p +1) ... (k +1)

Numeron n hajoaminen ensisijaisten lukumäärien tuotteena ja tieto siitä, kuinka monella jakautumisella on, sekä serkut että muut kuin muut, auttavat meitä määrittämään, mitkä nämä jakajat ovat.

Kun jokaisella on, paitsi viimeinen, jota ei vaadita summassa, voidaan tarkistaa, onko se täydellinen luku vai ei.

- Harjoitus 1

Varmista, että numero 28 on täydellinen.

Ratkaisu

Ensimmäinen on hajottaa luku sen päätekijöissä.

28 | 2
14 | 2
07 | 7
01 | 1

Sen jakajat ovat: 1, 2, 4, 7, 14 ja 28. Jos suljetaan pois 28, jakajien summa antaa:

Voi palvella sinua: puolet 15: stä

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Siksi 28 on täydellinen määrä.

Lisäksi kaikkien jakajien summa on 28 + 28 Joten sääntö σ (28) = 2 x 28.

- Harjoitus 2

Päättää, onko numero 38 täydellinen vai ei.

Ratkaisu

Numero on jaoteltu sen päätekijöihin:

39 | 3
13 | 13
01 | 1

39: n jakautuneet jakajat mukaan lukien itse: 1, 3 ja 13. Summa 1 + 3 + 13 = 4 + 13 = 17 ei ole yhtä suuri kuin 39, joten 39 on epätäydellinen tai ei-syksyinen numero. 

- Harjoitus 3

Selvitä, onko numero 120 täydellinen vai epätäydellinen.

Ratkaisu

Numero on jaoteltu sen päätekijöihin:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Päätekijöistä löytyy jakajia:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 ja 120

Jos 120 olisi täydellistä, kun lisätään kaikki sen jakajat 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Tämä tulos on selvästi erilainen kuin 240, joten päätellään, että numero 120 ei ole täydellinen luku.

- Harjoitus 4

Varmista, että euklidikriteerillä saatu numero 496 on täydellinen luku.

Ratkaisu

Numero 496 on jaoteltu sen päätekijöihin:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Sitten heidän jakajansa ovat:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Nyt kaikki ne lisätään, paitsi 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Vahvistaa, että se on todella täydellinen luku.

Viitteet

1. Baldor, a. 1986. Aritmeettinen. Codex -versiot ja jakaumat.
2. Kaikki päälukuista. Ystävienumerot. Toipunut: Sairaanhoitaja.org.
3. Wolfram Mathworld. Eulerin sääntö. Toipunut: MathWorld.Susi.com.
4. Wolfram Mathworld. Täydellinen numero. Toipunut: MathWorld.Susi.com.
5. Wikipedia. Täydelliset numerot. Haettu: vuonna.Wikipedia.org.
6. Wikipedia. Ystävienumerot. Palautettu: on.Wikipedia.org.