Järjestetty pari

Mikä on järjestetty pari?

Järjestetty pari tai duo Se on joukko kahta elementtiä, jotka on kirjoitettu tietyllä kriteerillä määritetyn määräyksen mukaisesti. Mainitut kriteerit määrittelevät, mitkä kahdesta elementistä menee ensin ja mikä seuraa sen jälkeen.

Tilattu pari on merkitty nimellä (x, y), missä "x" on parin ensimmäinen elementti ja "y" on toinen, jota kutsutaan myös Komponentit. Yleensä (x, y) se ei ole sama siisti vääntömomentti (y, x). Ja järjestyksen lisäksi toinen tilatujen parien tärkeä ominaisuus on tasa -arvo: kaksi tilattua paria (A, B) ja (C, D) ovat samat vain, jos A = C ja B = D.

Kuvio 1.- Tiivisten parien ansiosta koiranpentu tietää, että luut on haudattu paikkoihin (3,1) ja (-4,2), kun hänen talonsa on (0,0). Lähde: f. Zapata.

Esimerkkejä tilattuista pareista olisivat ikästä koostuvia ja matematiikan opiskelijoiden kurssia. Tilattu pari (15, 62) vastaa 15 -vuotiasta opiskelijaa, erilainen kuin epätodennäköinen pari (62,15).

Tilatun vääntömomentin käsite on erittäin tärkeä matematiikan eri alueilla, kuten Cartesian taso, fraktiot, vektorit tasossa, suhteet ja toiminnot. Tärkeä näkökohta on, että niiden elementeillä ei välttämättä ole numeerisia, esimerkiksi ne voidaan tilata seuraaville:

• Maalaiskaupunki
• Nimi sukunimi
• Vaimo aviomies

Ja monia muita yhdistelmiä.

Esimerkkejä tilattuista pareista

Fraktiot

Jakeella esitetään kahden P/Q -kokonaislukujen osamäärä, esimerkiksi osuus ½, joka vastaa desimaalin lukumäärää 0.5.

Tämä murto ei kuitenkaan ole ainoa, joka edustaa desimaalia 0.5, samoin seuraavat:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2)…

Tällä tavoin mikä tahansa murto voidaan esittää järjestetyksi pariksi (p, q), missä p ja q ovat kokonaisia, P: n miehittämisessä ja Q: n nimittäjän sijainti. On tärkeä rajoitus ja Q: n (nimittäjän) on oltava erilainen kuin 0, koska P/0 -muodon fraktioita ei ole määritelty.

Voi palvella sinua: äärellinen sarja: Ominaisuudet, esimerkit, ratkaisut harjoitukset

Ja toinen tärkeä ehto on, että kaksi fraktiota a/b ja c/d ovat yhtä suuret kuin on täytetyistä:

A ∙ d = b ∙ c

Toiminnot ja sen kaaviot

Funktio voidaan ilmaista siistinä pareina. Esimerkiksi kuvaamalla funktio Cartesian tasoon, ensimmäiselle elementille määritetään riippumattoman muuttujan sijainti, kun taas toiselle on määritetty riippuvainen muuttuja. Tämä on järjestetty pari.

Y = f (x) -toiminnolla siisti vääntömomentti voidaan ilmaista nimellä [x, f (x)]]. Harkitse esimerkiksi aloitusjoukkoa:

A = 1, 2, 3, 4

Tässä sarjassa on järjestetyn parin ensimmäiset komponentit y = x -toiminnon mukaan². Toisten komponenttien sarja on:

B = 1, 4, 9, 16

Ja tilatut parit muodostuvat: ovat:

(1,1); (2,4); (3, 9); (4; 16)

Ottaa huomioon.

Koneessa

Vektoreita voidaan edustaa karteesilasessa tilattujen parien avulla, joissa ensimmäinen elementti edustaa vaakasuoraa komponenttia "X" ja toinen pystysuora komponentti "Y". Vektorien erottamiseksi tason pisteistä, ne merkitään rohkeilla kirjaimilla ja neliömäitä käytetään sulujen sijasta, kuten tämä:

v =

Esimerkiksi vektori v = on vaakasuora komponentti yhtä suuri kuin 4 ja pystysuuntainen komponentti yhtä suuri kuin 7. Sen kuvaaja on:

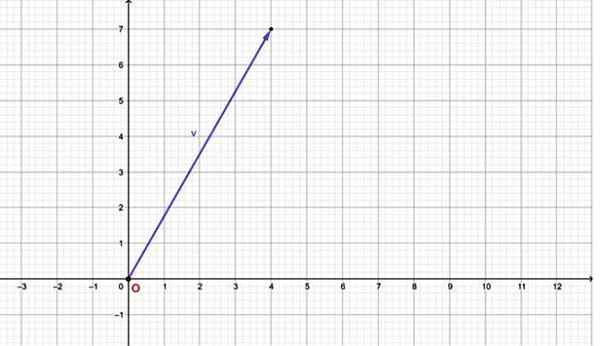Kuva 2.- Tasovektori voidaan ilmaista järjestetyn parin kautta. Lähde: f. Zapata.

Huomaa, että tällä vektorilla on alkuperä. Jos vektorilla on alkuperä missä tahansa muussa vaiheessa, se voidaan myös ilmaista järjestetyn vääntömomentin muodossa järjestettyjen parien kautta, katso seuraavat kohdat seuraavat kohdat.

Voi palvella sinua: operaatiohierarkia

Tilattu Pares -operaatiot

Lisäys

Olkoon kohteet (a, b) ja (c, d) parit (d). Uusi vääntömomentti saadaan sen summan avulla:

(a, b)+(c, d) = (a+c, b+d)

Neutraali elementti

Tilattujen parien lisäämisen neutraali elementti on vääntömomentti (0,0), koska kun se lisää tilattua paria (A, B), summa on jälkimmäinen:

(a, b) + (0,0) = (a, b)

Päinvastainen

Lisäämällä järjestetty pari (a, b) sen vastakkaisella (-a, -b), järjestetty vääntömomentti (0,0) saadaan:

(a, b) + (-a, -b) = (0,0)

Kommulatiivisuus

Lisäysten järjestys ei muuta summaa:

(a, b) + (c, d) = (c, d) + (a, b)

Assosiaatio

Kolmen tilatun parin lisäämisen tulosta ei muuteta ryhmiteltynä toiminnan suorittamiseen:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Tilattujen parien vähennys

Olkoon kohteet (a, b) ja (c, d), vähennys suoritetaan seuraavasti:

(a, b)-(c, d) = (a-c, b-d)

Tuote

Tuotteessa on kaksi vaihtoehtoa: i) Kerro vakiona tilattu vääntömomentti ja ii) kerrotaan kaksi (tai enemmän) siisteitä.

Kertolasku vakiona

Olkoon k vakio ja järjestetty vääntömomentti (a, b), vakion ja vääntömomentin välinen tuote on:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Tilattujen parien kertominen

Tilattujen parien (a, b) ja (c, d) välinen tuote suoritetaan seuraavasti:

(a, b) x (c, d) = (ac - bd, bc+ad)

Neutraali elementti

Kertolaskelman neutraali elementti on (1,0), koska kertomalla kaikki tällä tilatut vääntömomentit edellä kuvattujen kertolaskujen mukaisesti alkuperäinen vääntömomentti on:

(a, b) x (1,0) = (a - 0, b + 0) = (a, b)

Voi palvella sinua: moninkertainen käänteinen: Selitys, esimerkit, ratkaisut harjoitukset

Assosiaatio

Koska tekijöiden järjestys ei muuta tuotetta, se voidaan ryhmitellä eri tavoin moninkertaistaakseen kolme tai enemmän siistiä paria ja tulos on sama:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Ratkaisut

Harjoitus 1

Olet tilannut pareja (x², X-2) = (16, 2). Mikä on x: n arvo?

Ratkaisu

Tilattujen parien tasa -arvon soveltaminen saadaan ensin:

x² = 16 ⇒ x₁ = 4, x₂ = -4

Tietää, mitkä kahdesta arvosta valitsevat:

X-2 = 2

x = 2 + 2 = 4

Siksi x: n pyydetty arvo on 4.

Harjoitus 2

Ilmaise järjestelmällisenä pariliitoksena pisteestä (1, 3) pisteeseen (7, 11) ja edusta sitä graafisesti.

Ratkaisu

Olla v Vektori haki. Sitä edustavan järjestetyn parin määrittämiseksi ja sen koordinaatit sisältävät saapumispisteen ja alkuperäpisteiden koordinaatit vähennetään siinä järjestyksessä. Niin:

v = =

Sitten vektori on edustettuna v sellaisena, joka siirtyy (1,3) - (7, 11) ja laitteeseen v jonka alkuperä on kiinnitetty koordinaattijärjestelmän alkuperään (0,0). Kuten näette, heillä on sama suunta ja merkitys.

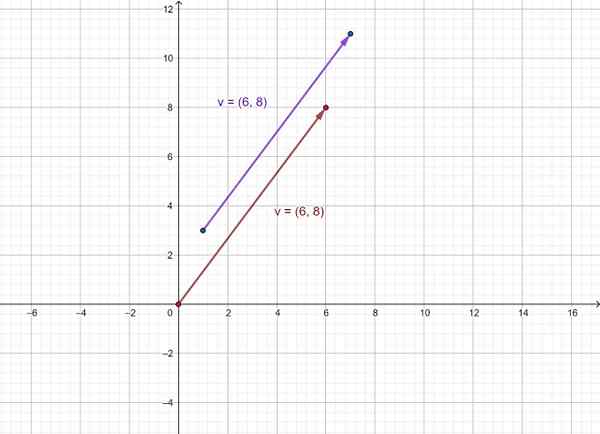Kuva 3. Vektorin esitys järjestetyksi pariksi. Lähde: f. Zapata.

Viitteet

1. Syventävä. Järjestetty pari. Toipunut: Deepai.org.
2. Matematiikka. Cartesian esitys vektorista järjestetyllä parilla. Toipunut: Matemovil.com.
3. Varsity -tutorit. Järjestetty pari. Haettu: WarsityTorm.com
4. Priestri, Juan. Suhteet ja toiminnot. Tekniikanalan tiedekunta. Matematiikan laitos. Buenos Airesin yliopisto. Haettu: Aiheet.fi.Uba.AR.
5. Denverin yliopisto. Suhteet. Toipunut: matematiikka.Ucdenver.Edu.