Ympyrän kehä kuinka saada se ulos ja kaavat, ratkaistut harjoitukset

Hän ympyrän kehä Se on joukko pisteitä, jotka muodostavat ympyrän muodon ja tunnetaan myös nimellä pituus ympärysmitta. Se riippuu säteestä, koska suuremmalla kehällä on selvästi suurempi muoto.

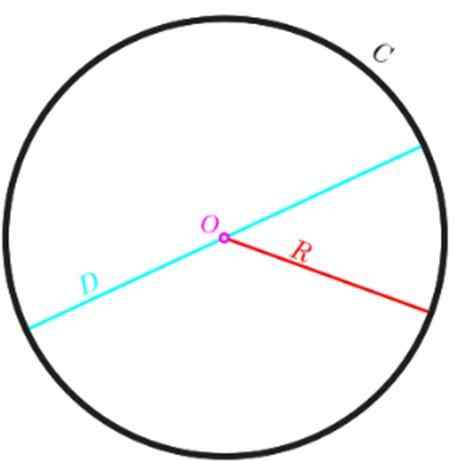
Olla P Ympyrän kehä ja R - saman säde, sitten voimme laskea P Seuraavan yhtälön kanssa:

P = 2π.R -

Ympyrän kehä (tässä tapauksessa pizza) riippuu sen radiosta. Lähde: Pixabay.

Missä π on todellinen numero (lukee "pi"), joka on noin 3 arvoinen.1416… Suspensat johtuvat siitä, että π: llä on ääretön desimaali. Siksi laskelmien tekemisessä on tarpeen pyöristää sen arvo.

Useimpien sovellusten osalta se riittää kuitenkin ottamaan tässä ilmoitetun määrän tai käyttämään kaikkia desimaaleja, jotka laskin, jolla se toimii.

Jos säteen sijasta on suositeltavaa käyttää halkaisijaa D, jonka tiedämme olevan kaksinkertainen säde, kehä ilmaistaan ​​seuraavasti:

P = π.2R = π.D -d

Koska kehä on pituus, se on aina ilmaistava yksiköissä, kuten metreissä, senttimetreissä, jalkoissa, tuumina ja muissa, riippuen parempana olevasta järjestelmästä.

[TOC]

Kehykset ja ympyrät

Ne ovat usein termejä, joita käytetään keskenään, ts. Synonyyminä. Mutta tapahtuu, että niiden välillä on eroja.

Sana "kehä" tulee kreikkalaisesta "ajanjaksosta", joka tarkoittaa muotoa ja "metroa" tai mittaa. Ympäristö on ympyrän ääriviivat tai kehä. Muodollisesti se on määritelty:

Ympyrä on pisteet, joiden etäisyys on yhtä suuri kuin keskusta, tämä etäisyys on kehän säde.

Ympyrä puolestaan ​​määritellään seuraavasti:

Ympyrä on pisteitä, joiden etäisyys keskustaan ​​nimeltään on pienempi tai yhtä suuri kuin kiinteä etäisyys, nimeltään radio.

Lukija voi varoittaa hienovaraisen eron molempien käsitteiden välillä. Ympäristö viittaa vain reunapisteisiin, kun taas ympyrä on pisteiden joukko reunasta sisäpuolelle, jonka ympärysmitta on raja.

Voi palvella sinua: Formula -selvitysharjoitukset

Harjoitukset jstk d -dYmpyrän kehän laskelman emostraatio

Seuraavien harjoitusten avulla kuvatut käsitteet toteutetaan käytännössä, samoin kuin jotkut muut, jotka selitetään sellaisenaan. Aloitamme yksinkertaisimmasta ja vaikeusastetta kasvatetaan asteittain.

- Harjoitus 1

Etsi 5 cm: n radioympyrän kehä ja pinta -ala.

Ratkaisu

Alussa annetusta yhtälöstä sovelletaan suoraan:

P = 2π.R -= 2π.5 cm = 10 π cm = 31.416 cm

Alueen laskemiseksi -Lla Käytetään seuraavaa kaavaa:

-Lla = π.R -² = π. (5cm)²= 25π cm²= 78.534 cm²

- Harjoitus 2

a) Etsi seuraavan kuvan tyhjän alueen kehä ja pinta -ala. Varjostetun ympyrän keskipiste on punaisessa pisteessä, kun taas valkoisen ympärysmitta on vihreä piste.

b) Toista varjostetun alueen edellinen osa.

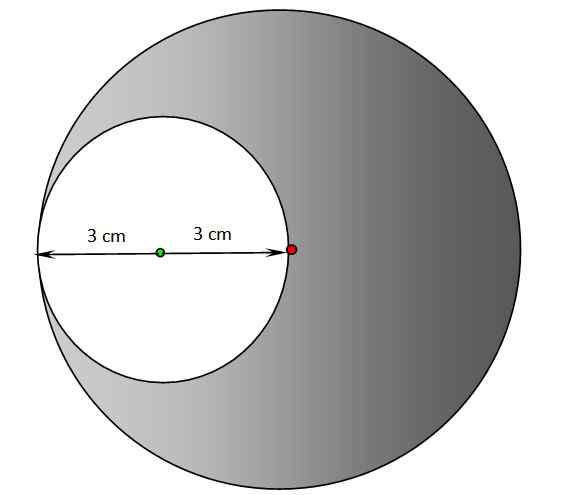Ympyrät harjoitukselle 2. Lähde: f. Zapata.

Ratkaisu

a) Valkoisen kehän säde on 3 cm, joten käytämme samoja yhtälöitä kuin harjoituksessa 1:

P = 2π.R -= 2π.3 cm = 6 π cm = 18.85 cm

-Lla = π.R -² = π. (3cm)²= 9π cm²= 28.27 cm²

b) Varjostetussa ympyrässä säde on 6 cm, sen kehä on kaksinkertainen osassa A laskettu):

P = 2π.R -= 2π.6 cm = 12 π cm = 37.70 cm

Ja lopuksi varjostetun alueen pinta -ala lasketaan seuraavasti:

- Ensimmäinen on varjostetun ympyrän alue ikään kuin se olisi valmis, jota kutsumme ', näin:

To ' = π.R -²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Sitten alueelle To ' Valkoisen ympyrän alue on vähennetty, aikaisemmin osiossa A), tällä tavalla pyydetty alue saadaan, joka merkitään yksinkertaisesti seuraavasti:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Harjoitus 3

Etsi varjostetun alueen alue ja kehä seuraavasta kuvasta:

Voi palvella sinua: Lisäkulmat: Mitä ovat, laskenta, esimerkit, harjoitukset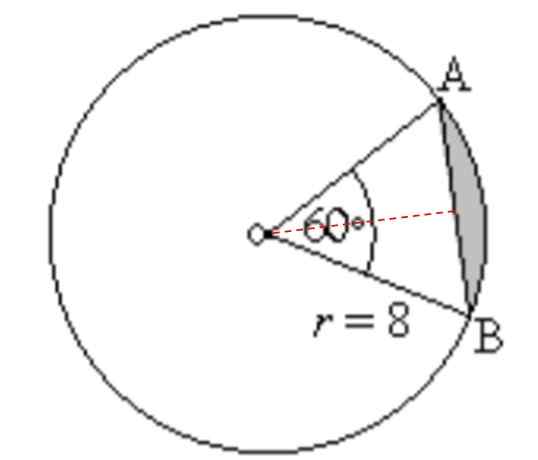Harjoituksen 3 kuva. Lähde: f. Zapata.

Ratkaisu

Varjostetun alueen pinta -alan laskenta

Laskemme ensin alueen Pyöreä sektori tai kiila, suorien segmenttien OA ja OB: n ja pyöreän AB -segmentin välillä, kuten seuraavassa kuvassa esitetään:

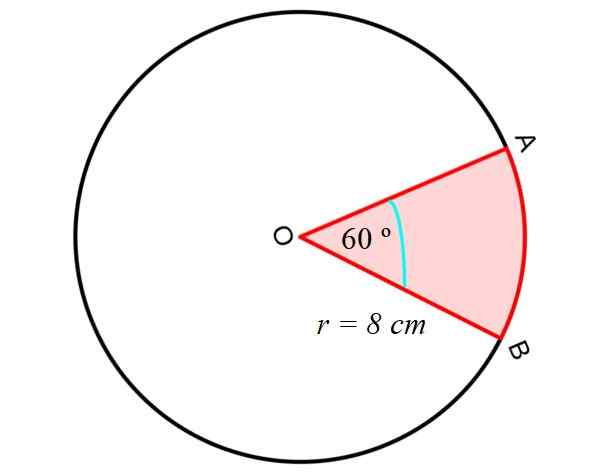
Tätä varten käytetään seuraavaa yhtälöä, joka antaa meille pyöreän sektorin pinta -alan, joka tuntee säteen R ja OA- ja OB -segmenttien välinen keskikulma, toisin sanoen kaksi kehän radiosta:

-Lla _{Pyöreä sektori} = Π.R -². (αº/360º)

Missä αº on keskikulma - se on keskeinen, koska sen kärki on kehän keskipiste - kahden radiossa.

Vaihe 1: Pyöreän sektorin pinta -alan laskenta

Tällä tavalla kuvassa esitetyn sektorin pinta -ala on:

-Lla _{Pyöreä sektori} = Π.R -². (αº/360º) = π. (8 cm-A². (60º/360º) = (64/6) π cm²= 33.51 cm²

Vaihe 2: Kolmion alueen laskenta

Sitten laskemme kuvan 3 valkoisen kolmion alueen. Tämä kolmio on tasa -arvoinen ja sen alue on:

-Lla _kolmio = (1/2) pohja x korkeus

Korkeus on kuvassa 4 nähty katkoviivainen punainen viiva. Jos haluat löytää sen, voit käyttää esimerkiksi Pythagoras -lausetta. Mutta se ei ole ainoa tapa.

Observer -lukija on huomannut, että tasasivuinen kolmio on jaettu kahteen identtiseen suorakulmioon, joiden emäs on 4 cm:

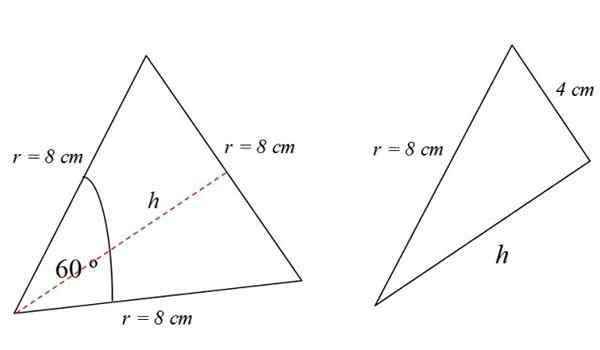
Oikeassa kolmiossa Pythagoras -lause täyttyy, siksi:

Koska sinulla on kolmion korkeus, sekä suorakulmio että tasapaino, sen pinta -ala on laskettu:

-Lla _kolmio = (1/2) Pohja x korkeus = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Vaihe 3: Varjostetun alueen laskenta

Se riittää vähentämään vähäisen alueen (tasapainon kolmion alue) tärkein alue (pyöreän sektorin alue): a _{varjostettu alue} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Varjostetun alueen kehän laskenta

Haettu kehä on 8 cm: n suoraviivaisen puolen ja AB -kehän summa kaari.  Täydellinen ympärysmitta on kuitenkin 360 º, siksi kaari, joka subtes 60 º on kuudes osa koko pituutta, jonka tiedämme olevan 2.π.V:

Voi palvella sinua: Kasvava toiminto: Kuinka tunnistaa se, esimerkkejä, harjoituksia

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Korvattu, varjostetun alueen kehä on:

P = 8 cm + 8.38 cm = 16.38 cm.

Sovellukset

Kehyre.

Taiteilijat, suunnittelijat, arkkitehdit, insinöörit ja monet muut ihmiset hyödyntävät kehää kehittäessään työtä, etenkin ympyrän, koska pyöreä muoto on kaikkialla: mainonnasta, ruoan kautta koneisiin.

Ympäristö ja ympyrä ovat eniten käytettyjä geometrioita. Lähde: Pixabay.

Tietääksesi suoraan ympyrän pituuden, se riittää käärittämään sen kierteellä tai merkkijonolla, laajenna sitten tämä lanka ja mittaa se teipillä. Toinen vaihtoehto on mitata ympyrän säde tai halkaisija ja käyttää joitain yllä kuvattuja kaavoja.

Päivittäisessä työssä kehäkonseptia käytetään:

-Asianmukainen muotti valitaan tietylle pizzalle tai kakun koosta.

-Kaupunkitie suunnitellaan laskemalla redoman koon, jossa autot voivat kääntyä muuttamaan merkitystä.

-Tiedämme, että maa pyörii auringon ympärillä suunnilleen pyöreällä kiertoradalla -todellisuudessa planeetta kiertoradat ovat elliptisiä, Keplerin lakien mukaan -mutta ympärysmitta on erittäin hyvä lähestymistapa useimpiin planeetoihin.

-Verkkokaupasta ostettavan renkaan tai renkaan sopiva koko on valittu.

-Valitsemme avaimen oikean kokoiseen mutterin löysäämiseen.

Ja paljon muuta.

https: // youtu.Be/cr8xjryl5tk

Viitteet

1. Ilmaiset matematiikan opetusohjelmat. Ympyrän alue ja kehä - geometrian laskin. Palautettu: Analysemath.com.
2. Matematiikan avoin viite. Ympyrä, ympyrän kehä. Toipunut: MathPenref.com.
3. Monterey Institute. Kehä ja alue. Toipunut: Montereyinstitute.org.
4. Tiede. Kuinka löytää ympyrän kehä. Toipunut: tiedekunnasta.com.
5. Wikipedia. Ympärysmitta. Haettu: vuonna.Wikipedia.org.