Kuusikulmainen pyramidi

Kuvio 1. Vasemmalla kuusikulmainen pyramidi ja oikealle sen seitsemän sivua otettiin käyttöön lentokoneessa: kuusikulmaisen pohjan keskellä ja kuuden kolmion muotoisen kasvojen ympärillä. Lähde: f. Zapata.

Mikä on kuusikulmainen pyramidi?

Kuusikulmainen pyramidi on kolmen dimensioinen geometrinen hahmo, jonka pohja Se on kuusikulmio (kuusipuolinen monikulmio) ja siinä on myös kuusi kasvot kolmionmuotoisesti, jotka on kerätty tietylle pohjan korkeudelle, nimeltään kohdassa kärki jompikumpi kärki.

Kuusikulmaisella pyramidilla on yhteensä seitsemän pintaa, jos pohja on sivun sivu, joten se on myös monimuotoinen Heptaedroni, Kreikan kielestä johdettu sana ("hep" tarkoittaa seitsemää).

Jos sivujen muodostavat kolmiot ovat samoitusmuotoja, ts. Niillä on kaksi yhtä suurta puolta ja yksi erilainen, se on a suora pyramidi. Ja jos pohjan kuusikulmio on säännöllistä, niin se on a Säännöllinen kuusikulmainen pyramidi, Kuten kuvassa 1 esitetään.

Kun pohjan kuusikulmio ei ole säännöllinen tai kasvot muodostavat kolmiot eivät ole samoja, on a Oblicual kuusikulmainen pyramidi.

Kuusikulmaisen pyramidin ominaisuudet

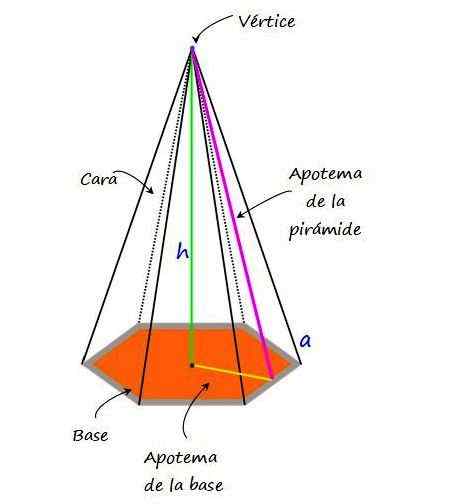Kuva 2.- Kuusikulmainen pyramidi ja sen pääelementit. Lähde: f. Zapata.

Kuusikulmaisen pyramidin pääominaisuudet ja elementit ovat seuraavat:

-Pohja, Se on kuusikulmio, joka voi olla säännöllinen tai epäsäännöllinen.

-Kasvot, Heillä on kolmion muoto ja yhteensä 6.

-Kärki tai kärki pyramidi, Kuuden kolmion muotoisen kasvojen sattumakohta.

-Reuna, segmentti, jossa kaksi pyramidi kasvot ovat samat. Se sivureunat Ne ovat sivuttaisten kasvojen sattuma -segmenttejä, kun taas pohjan reunat ovat segmentit, joissa kuusikulmion puoli tapahtuu ja viereisen kolmion toinen puoli. Kuvassa 2 reuna merkitään kirjaimella "a".

Voi palvella sinua: Divisions, jossa jäännös on 300

-Korkeus, "H" merkittynä, se on etäisyys, joka mitataan kärjestä pyramidin pohjaan.

-Pyramidi, Segmentti, joka liittyy kärkipisteeseen keskipisteen kanssa pohjan toisella puolella.

-Pohjapohja, Se määritetään vain, kun kuusikulmio on säännöllinen. Se koostuu segmentistä, joka liittyy kuusikulmion keskustaan ​​sen sivun keskustaan.

Alueen ja tilavuuden kaavat

Kuusikulmaisen pyramidin pinta -ala, joko säännöllinen tai epäsäännöllinen, lasketaan lisäämällä sivupintojen alueet ja kuusikulmaisen pohjan pinta -ala:

A = a_pohja + ∑a_{kallis sivu-}

Kaavassa ”∑” -symboli edustaa summaa, jotta voidaan tehdä yhteenveto sivupinnan kuuden alueen summasta.

Tavalliselle kuusikulmaiselle pyramidille on kaava löytää alueen:

A = 3L ∙ (AP_pohja + AP_pyramidi-A

Missä:

• L on pohjan reuna (kuusikulmion puoli).
• AP_pohja Se on pohjan apoteemi
• AP_pyramidi Se on pyramidin apotemi.

Jos pyramidi ei ole säännöllinen joko siksi, että pohja ei ole tavallinen kuusikulmainen tai koska pyramid.

Tavallisella kuusikulmaisella pyramidilla on myös kaava tilavuudelle:

V = l ∙ AP_pohjaH

Täällä "H" edustaa pyramidin korkeutta.

Ja jos kuusikulmainen pyramidi ei ole säännöllinen, kaikki pyramidit sovelletaan yleinen kaava sen tilavuuden laskemiseksi:

V = ⅓ ∙ a_pohja H

Se voi palvella sinua: Luonnollisten lukujen hajoaminen (esimerkit ja harjoitukset)

Numeerinen esimerkki

Tavalliselle kuusikulmaiselle pyramidille, jonka mitat ovat:

Perusapoteemi: 4 cm

Pohjareunan pituus: 7 cm

Pyramid Apoteme: 15 cm

Korkeus: 10 cm

Laske seuraava:

a) kuusikulmainen pohjaalue.

b) Pyramidin pinta -ala.

c) tilavuus

Liittää jhk

Tavanomaisen kuusikulmion alue on:

A = ½ (kehä × apotema) = ½ (6L × AP_pohja-A

A = 3L ∙ AP_pohja  = 3 × 7 cm × 4 cm = 84 cm²

Ratkaisu b

A = 3L ∙ (AP_pohja + AP_pyramidi) = 3L ∙ AP_pohja  + 3L ∙ AP_pyramidi = 84 cm² + (3 × 7 cm × 15 cm) = 399 cm².

Liuos C

Volume löytyy yleiskaavasta:

V = ⅓ ∙ a_pohja ∙ H = ⅓ ∙ 84 cm² ∙ 10 cm = 280 cm³

Kuinka tehdä kuusikulmainen pyramidi?

Materiaalit

• Paperi, pahvi tai pahvi.
• Sääntö- ja ryhmä
• Grafiittikynä ja värilliset merkinnät
• Sakset
• Liima käsitöistä.

Menettely

1. Siirrä alla oleva malli, halutulla mittakaavassa, pahvissa tai pahvissa, grafiittikynän, säännön ja joukkueen avulla. Toinen vaihtoehto on kopioida kuva asiakirjatyypiksi tai muokattavaksi piirtämiseksi ja suurentaminen, kunnes sinulla on halutut mitat.
2. Kun malli on siirtynyt paperiin tai pahviin, se on leikattava erittäin huolellisesti.
3. Taivuta nyt katkoviivoja pyramidin muotoilemiseksi varmistaen, että sivut sopivat oikein.
4. Taita myös ripset, varmista, että ne sopivat hyvin ja lisäävät sitten liimaa, painamalla niitä huolellisesti niin, että ne ovat paikoillaan, muotoilemalla hahmoa.
5. Koristele pyramidi värillisillä merkinnöillä.

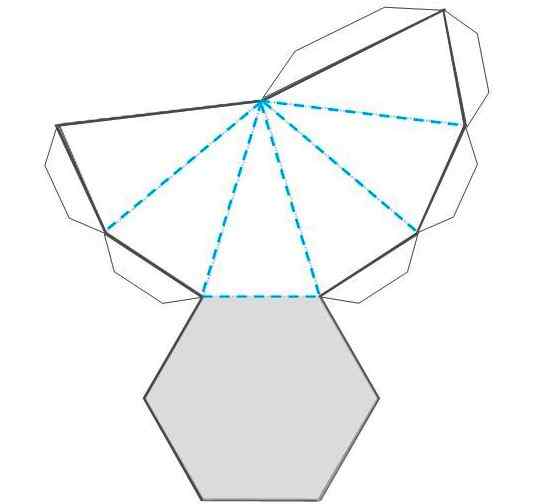Kuva 3.- Malli kuusikulmaisen pyramidin leikkaamiseksi ja kokoamiseksi. Lähde: f. Zapata.

Esimerkkejä kuusikulmaisista pyramideista

Pohja -kuusikulmion mukaan kuusikulmaiset pyramidit voivat olla:

Voi palvella sinua: Algebrallinen kieli: Konsepti, mihin se on, esimerkkejä, harjoituksia

-Kupera, Jos kaikki kuusikulmion sisäkulmat ovat alle 180º.

-Kovera, Jos yksi tai useampi kuusikulmion sisäkulmista on yli 180º.

Kuvion 1 tavallinen kuusikulmainen pyramidi on kupera, koska kaikki emäksen sisäiset kulmat mittaavat alle 180º. Tarkemmin sanottuna tavallisen kuusikulmion sisäkulmat mittaavat kaikki 120º.

Tämän mukaan kuusikulmaisten pyramidien muoto vaihtelee, kuten silloin on esitetty.

Oblicual kuusikulmainen pyramidi

Kuvion 4 kuvassa havaitaan vino kuusikulmainen pyramidi, jonka pohja on säännöllinen. Huomaa, että etualalla olevat kasvot muodostavat kolmio, on kolmio, jolla on kolme eri puolta (Scaleen -kolmio), toisin kuin kuvan 1 pyramidi, jonka kasvot ovat samaskles -kolmioita. Jos viiva on piirretty kärkipisteestä kuusikulmion keskustaan, se osoittautuu kaltevaksi pystysuoraan nähden.

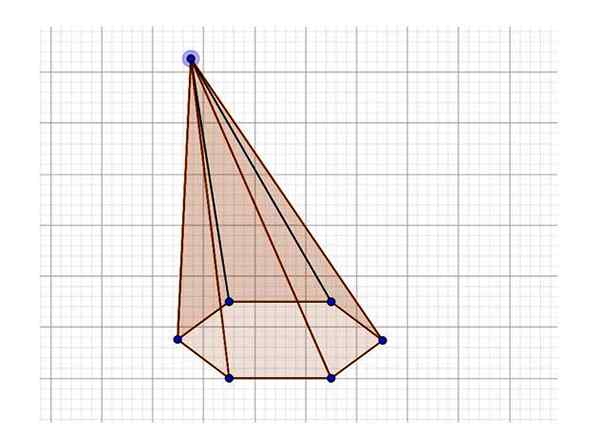Kuva 4. Esimerkki vinoista kuusikulmaisesta pyramidista. Lähde: f. Zapata Geogebran kautta.

Kovaa ja vino kuusikulmainen pyramidi

Tämän kuusikulmaisen pyramidin perusta sisältää sisäkulman, jonka mitta on suurempi kuin 180º, siksi se on kovera pyramidi, vinojen lisäksi.

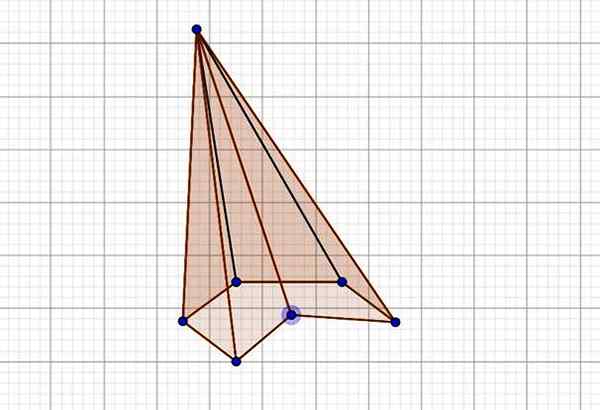Kuva 5. Vino ja kovera kuusikulmainen pyramidi. Lähde: f. Zapata Geogebran kautta.