Hydrostaattinen painekaava, laskenta, esimerkit, harjoitukset

Se Hydrostaattinen paine Se on se, joka käyttää nesteen staattisessa tasapainossa missä tahansa sisällä, joko siihen upotettu alue, säiliön seinät tai osa nestettä, joka on osa kokonaismassaa.

Tapa, jolla nesteet kohdistavat painetta, eroaa kiinteistä aineista. Nämä aiheuttavat painetta, mutta neste tai kaasu tekevät niin kaikkiin suuntiin.

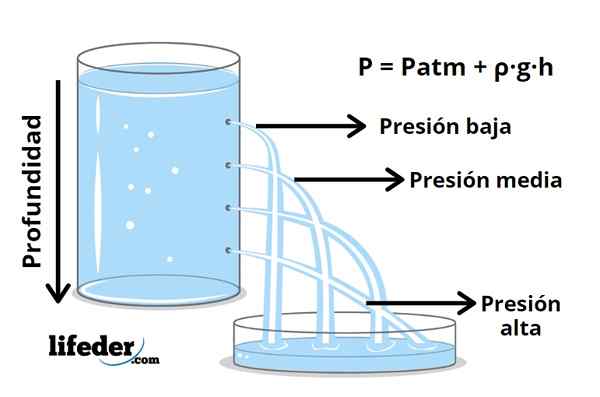
Kuva 1- Suuremmalla paineella

Nesteen suhteen paine nousee syvyyden myötä, kuten kokemuksen tiedetään upottaessaan veteen, johon paineesta nousee korvissa. Tämä paine tulee nesteen painosta ja sen muodostavien hiukkasten lakkaamattomasta liikkeestä, jotka jatkuvasti osuvat nesteeseen upotettujen kehon pintaan.

Jos oletamme puristamattoman nesteen - mikä on totta suurimmassa osassa sovelluksia, - sen tiheys pysyy vakiona ja siinä tapauksessa paine riippuu lineaarisesti syvyydestä.

[TOC]

Kaava

Hydrostaattinen paine lasketaan seuraavalla lausekkeella:

P = p_{Pankkiautomaatti} + ρ · g · h

Missä:

-P Paine kohdistuu pisteeseen

-P_{Pankkiautomaatti} Se on ilmakehän paine vapaaseen pintaan

-ρ on nestetiheys

-G on painovoiman kiihtyvyys

-H on syvyys, johon haluat laskea hydrostaattisen paineen 

Kaava sisältää ilmakehän vaikutukset, mutta monet paine tai manometrit asettavat 0 ilmakehän paineeseen, tästä syystä ne mittaavat paine tai suhteellinen paine, jota kutsutaan myös mittaripaine-

P_m = ρ · g · h

Kaasujen suhteen ne puristetaan tai laajennetaan erittäin helposti. Siksi sen tiheys, joka on syy massan ja tilavuuden välillä, on yleensä muiden parametrien, kuten korkeuden ja lämpötilan funktio, ilmakehän kaasujen tapauksessa.

Se voi palvella sinua: magnetointi: kiertoradan ja spin -magneettinen momentti, esimerkkejä

Painetta, jota kaasujen käyttäminen yleensä kutsutaan aerostaattinen paine, termi hydrostaattinen paine varattuille nesteille.

Hydrostaattiset paineesimerkit

Hydrostaattinen paine riippuu vain syvyydestä, joten säiliön pohjan muoto tai pinta -ala ei ole merkityksellinen.

Koska P -paine määritellään voiman F kohtisuoraan komponenttiin alueen A yksikköä kohti:

P = f/a

Sitten säiliön alaosaan kohdistama neste kohdistuu erilainen, mutta jakautuu eri pidennyksille, paine, joka on voiman/alueen suhde, on sama samaan syvyyteen kohdistuville pisteille.

Harkitse kuvan säiliöitä. Paine on sama kaikille punaisille pisteille, jotka ovat samalla tasolla, vaikka kyseisen tason yläpuolella on suurempi määrä keskustassa -enemmän leveyteen -, joista on lieriömäinen ja ohut putki äärimmäisen vasemman.

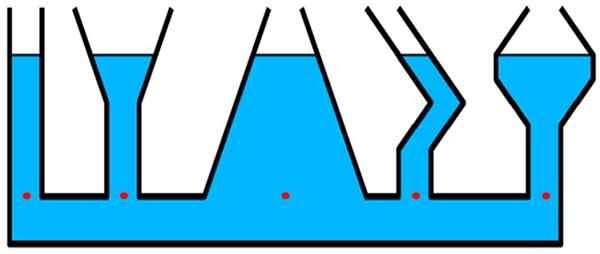Kuva 2.- Paine missä tahansa punaisessa pisteessä on sama, säiliön muodosta riippumatta. Lähde: Wikimedia Commons.

Rakenteet, joissa hydrostaattinen paine on merkityksellinen

-Padon seinät: Vaikka voima on sama tasaisen pohjan kaikille pisteille, pystysuunnassa se kasvaa syvyyden kasvaessa, joten tukiseinät ovat pohjassa leveämpiä kuin yläosassa.

-Uima -altaan seinillä ja pohjalla.

-Tähteissä kuten aurinko, jossa hydrostaattinen paine tasapainottaa painovoiman ja pitää tähden toiminnassa. Kun mainittu tasapaino on katkaistu, tähti romahtaa ja kärsii äärimmäisistä muutoksista rakenteessaan.

Voi palvella sinua: mikä on magneettinen hetki?

-Nestemäiset varastosäiliöt, jotka on suunniteltu kestämään hydrostaattista painetta. Ei vain seinät, vaan myös portit, jotka helpottavat täyttämistä ja uuttamista. Suunnittelussaan se otetaan huomioon, jos neste on syövyttävä ja myös paine ja pakottaa, että se käyttää tiheyden mukaan.

-Renkaat ja ilmapallot, jotka ovat tartunnan saaneet siten, että ne kestävät nestepainetta (kaasua tai nestettä) repimättä.

-Mikä tahansa upotettu runko, joka kokee pystysuoran työntövoiman tai "helpotuksen" painon, nesteen aiheuttaman hydrostaattisen paineen ansiosta. Tämä tunnetaan nimellä Archimedesin periaate.

Harjoitukset

Archimedes -periaate vahvistaa, että upottamalla ruumiin kokonaan tai osittain se kokee pystysuoran voiman, joka tunnetaan nimellä työntövoima. Työntövoiman suuruus on numeerisesti yhtä suuri kuin esineen siirtämän veden tilavuuden paino.

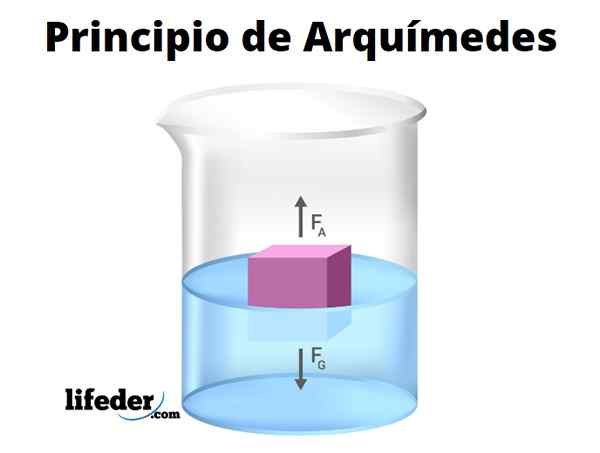
Olla ρ_sujuva Nesteen tiheys, v_s Upotettu tilavuus, G painovoiman kiihtyvyys ja b työntövoiman suuruus, jonka voimme laskea seuraavalla lausekkeella:

B = ρ_sujuva .V_s .g

- Harjoitus 1

Suorakaiteen muotoinen lohko, jonka mitat ovat 2.0 cm x 2.0 cm x 6.0 cm kelluu makeassa vedessä pisin pystysuora akseli. Veden yläpuolella erottuneen lohkon pituus on 2.0 cm. Laske lohkon tiheys.

Ratkaisu

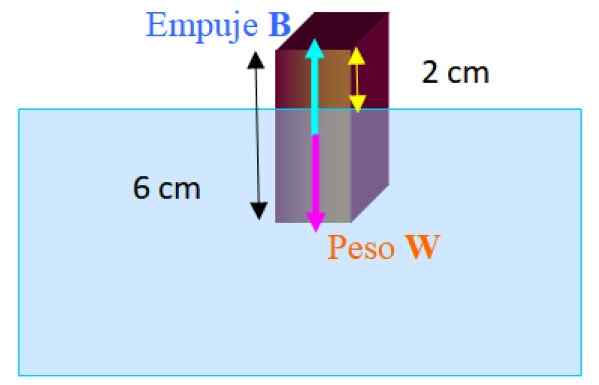Kuva 3.- Vapaa runkokaavio lohkolle, joka kelluu osittain upotettuna veteen. Lähde: f. Zapata.

Lohkoon vaikuttavat voimat ovat paino W - alaspäin ja työntövoima B - ylöspäin. Kun lohko kelluu tasapainossa, sinulla on:

∑ f_ja = B - W = 0

B = w

Painon W -suuruus on lohkon massa M: n tuote painopisteen kiihtyvyyden vuoksi. Käytämme tiheyden määritelmää ρ_jompikumpi Kuten messun välinen osuus m ja tilavuus V lohko:

Voi palvella sinua: Mesheal -analyysi: Käsitteet, menetelmät, esimerkit

ρ_jompikumpi = m / v → m = ρ_jompikumpi . V

Pyöritys puolestaan ​​on:

B = ρ_sujuva .V_s .g

Painon työntövoiman ja suuruuden tasoitus:

ρ_sujuva .V_s .G = ρ_jompikumpi . V.g

Painovoima peruutetaan siitä, että se on molemmin puolin tekijä ja lohkon tiheys voidaan tyhjentää seuraavasti:

ρ_jompikumpi = ρ_sujuva . (V_s  / V)

Vesitiheys kansainvälisissä järjestelmäyksiköissä on 1000 kg/m³. Kokonais Volumes ja upotettu V_s, Ne lasketaan v = leveys x korkea x syvyys:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

V_s = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Arvojen korvaaminen:

ρ_jompikumpi = ρ_sujuva . (V_s  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Harjoitus 2

Laske merivedessä kelluvan jääveden upotettu tilavuusprosentti 0 ºC: seen.

Ratkaisu

Jää kelluu vedessä, koska sen tiheys on pienempi: 916.8 kg/m³, mikä tarkoittaa, että se laajenee, kun se jäähtyy, toisin kuin useimmat aineet, että lämmittäessään ne lisäävät heidän tilavuutensa.

Kuva 4. Lähes koko jäävuoren osa pysyy upotettuna. Lähde: Pixabay.

Se on erittäin onnekas olosuhde elämälle, siitä lähtien vesimassat jäätyen vain pinnalla, pysyvä neste syvyydessä.

Meriveden tiheys on hiukan suurempi kuin makean veden: 1027 kg/m³. Laskemme tilavuusosan v_s  / V:

V_s  / V = ​​ρ_jompikumpi / ρ_sujuva = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

Tämä tarkoittaa, että noin 89 % jäätä pysyy upotettuna veden alla. Vain 11 % on näkyvissä kelluvalla merellä.

Viitteet

1. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
2. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
3. Cimbala, c. 2006. Nesteiden, perusteiden ja sovellusten mekaniikka. MC. Graw Hill.
4. Hibbeler, R. 2015. Fluidimekaniikka. Ensimmäinen. Ed. Pearson.
5. Mott, r.  2006. Fluidimekaniikka. Neljäs. Painos. Pearson -koulutus.
6. Streeter, v. 1999. Fluidimekaniikka. McGraw Hill.