Trapetsoidinen prisma

Mikä on trapetsoidinen prisma?

Eräs Trapetsoidinen prisma Se on prisma siten, että mukana olevat monikulmiot ovat trapezoideja. Prisman määritelmä on geometrinen runko, joka muodostuu kahdesta yhtä suuresta ja yhdensuuntaisesta monikulmusta toistensa kanssa, ja loput niiden kasvoista ovat yhdensuuntaisia ​​ohjelmia.

Prismalla voi olla erilaisia ​​muotoja, jotka eivät riipu pelkästään monikulmion sivujen lukumäärästä, vaan itse monikulmiosta.

Jos prisman monikulmiot ovat neliömäisiä, niin tämä eroaa prismasta, johon sisältyy esimerkiksi rhombuksia, huolimatta siitä, että molemmilla monikulmioilla on sama määrä sivuja. Siksi se riippuu siitä, mitä kvadrilateriaali.

Trapetsoidisen prisman ominaisuudet

Nähdäksesi trapetsoidisen prisman ominaisuudet, sinun tulisi aloittaa tietämällä, miten se vedetään, niin mitä ominaisuuksia pohja kohtaa, mikä on pinnan pinta -ala ja lopulta kuinka sen tilavuus lasketaan.

1. Piirrä trapezoidinen prisma

Piirrä se on ensin määritettävä, mikä trapetsi on. Trapetsi on neljän sivun epäsäännöllinen monikulmio (kvadrilateraalinen), mutta siten, että sillä on vain kaksi yhdensuuntaista puolta, jota kutsutaan emäkseksi ja sen emäksen välistä etäisyyttä kutsutaan korkeuteen.

Piirrä suora trapetsoidinen prisma, alat piirtää trapezoidia. Sitten jokaisesta pystysuorasta viivasta, jonka pituus “H” on projisoitu jokaisesta vertistä ja lopulta vedetään toinen trapetsoidi, että sen kärkipisteet vastaavat aikaisemmin piirrettyjen viivojen päätä.

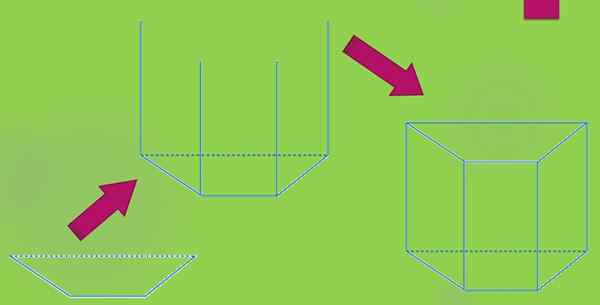
Sinulla voi olla myös vino trapetsoidinen prisma, jonka rakenne on samanlainen kuin edellinen, sinun on vain piirrettävä neljä yhdensuuntaista viivaa keskenään.

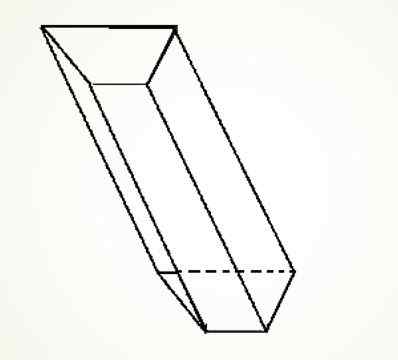
2. Trapetsin ominaisuudet

Kuten aiemmin todettiin, prisman muoto riippuu monikulmiosta. Trapetsin erityistapauksessa löydämme kolme erityyppistä emäksiä:

Suorakaiteen trapetsi: Se on se, että trapetsi, jolla yksi sen sivuista on kohtisuorassa rinnakkaisten sivujensa suhteen tai että yksinkertaisesti on suorakulma.

Trapezium -sammutus: Se on trapetsoidi, jolla sen ei -rinnakkaiset sivut ovat samanpituisia.

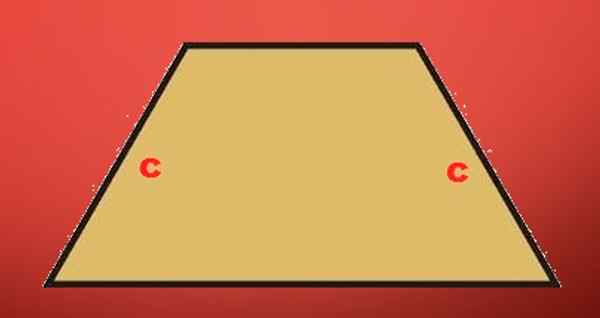
Escaleno trapezio: Trapetsia ei ole yhtä suuri tai suorakulmio; Sen neljällä sivulla on eri pituus.

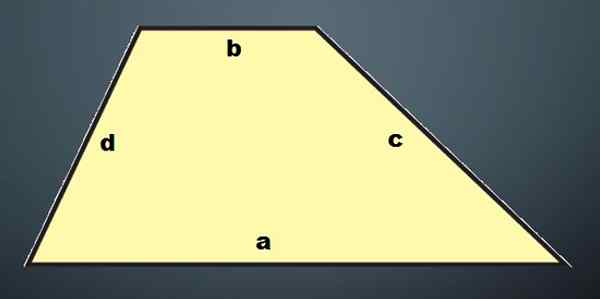
Kuten voidaan nähdä, käytetyn trapetsin tyypin mukaan saadaan erilainen prisma.

3. Pinta-ala

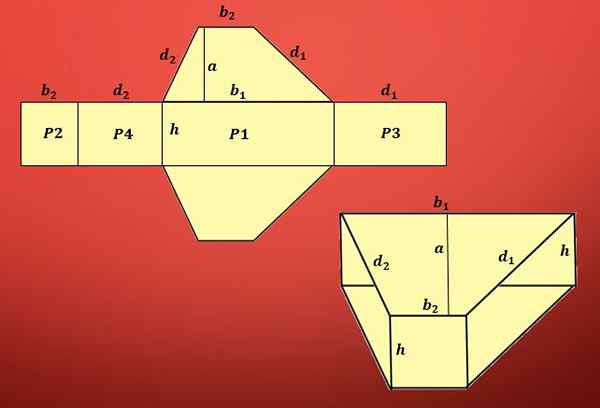
Matsakkeisen prisman pinnan pinta -alan laskemiseksi meidän on tiedettävä trapetsoidin pinta -ala ja kunkin rinnakkaisohjelman pinta -ala.

Kuten kuvassa voidaan nähdä, alue sisältää kaksi trapetsia ja neljä erilaista rinnakkaista.

Trapetsin pinta -ala on määritelty t = (b1+b2) xa/2 ja rinnakkaisogrammien alueet ovat P1 = Hxb1, P2 = Hxb2, P3 = Hxd1 ja P4 = Hxd2, missä “B1” ja “B2 "Ovat trapetsoidin," d1 "ja" d2 "emäkset.

Siksi trapetsoidisen prisman pinnan pinta -ala on A = 2T+P1+P2+P3+P4.

4. Tilavuus

Koska prisman tilavuus on määritelty V = (monikulmioalue) x (korkeus), voidaan päätellä, että trapetsoidisen prisman tilavuus on v = txh.

5. Sovellukset

Yksi yleisimmistä esineistä, joilla on trapetsoidisen prisman muoto.