Ehdollinen todennäköisyyskaava ja yhtälöt, ominaisuudet, esimerkit

Se ehdollinen todennäköisyys Se on tietyn tapahtuman esiintymismahdollisuus, koska toinen tapahtuu ehtona. Nämä lisätiedot voivat muokata (tai ehkä) käsitystä, että jotain tapahtuu.

Voimme esimerkiksi kysyä itseltämme: ”Mikä on todennäköisyys, että sataa tänään, koska kaksi päivää sitten se ei sataa?". Sen tapahtuma, jonka haluamme tietää todennäköisyyden, on se, että se sataa tänään, ja lisätiedot, jotka vastaavat vastausta, on, että "kaksi päivää sitten se ei sataa".

Kuvio 1. Todennäköisyys, että sataa tänään, koska eilen satoi on myös esimerkki ehdollisesta todennäköisyydestä. Lähde: Pixabay.

Olla Todennäköisyystila koostuu ω (näytetila), ℬ (satunnaiset tapahtumat) ja p (kunkin tapahtuman todennäköisyys) sekä tapahtumat A ja B, jotka kuuluvat ℬ.

Ehdollinen todennäköisyys, joka tapahtuu, koska B, joka on merkitty nimellä P (A│B), määritellään tällä tavalla:

P (a│b) = p (a∩b) / p (b) = p (a ja b) / p (b)

Missä: P (A) on A: n, p (b): n esiintymisen todennäköisyys on tapahtuman B todennäköisyys ja se on erilainen kuin 0 ja p (A∩B) on A: n ja B: n risteyksen todennäköisyys, eli se on , todennäköisyys, että molemmat tapahtumat tapahtuvat (yhteinen todennäköisyys).

Tämä on ilmaus Bayes -lauseelle, jota sovellettiin kahteen tapahtumaan, joita englantilainen teologi ja matemaatikko Thomas Bayes ehdotti vuonna 1763.

[TOC]

Ominaisuudet

-Kaikki ehdollinen todennäköisyys on välillä 0 ja 1:

0 ≤ p (a│b) ≤ 1

-Todennäköisyys, että tapahtuma tapahtuu, koska tämä tapahtuma tapahtuu, on selvästi 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Jos kaksi tapahtumaa ovat yksinoikeudella, ts. Tapahtumat, jotka eivät voi tapahtua samanaikaisesti, ehdollinen todennäköisyys, että yksi niistä tapahtuu, on 0, koska risteys on tyhjä:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Jos B on A: n osajoukko, niin ehdollinen todennäköisyys on myös 1:

Voi palvella sinua: Toroid tai Toro Dona

P (b│a) = p (a∩b) / p (a) = 1

Tärkeä

P (A│B) Se ei yleensä ole yhtä suuri kuin P (B│A), joten sinun on huolehdittava siitä, ettet vaihda tapahtumia ehdollisen todennäköisyyden löytämisessä.

Yleinen kertolasku

Monta kertaa haluat löytää niveltodennäköisyyden P (A∩B) ehdollisen todennäköisyyden sijasta. Joten seuraavan lauseen kautta:

P (a∩b) = p (a ja b) = p (a│b). P (b)

Lausetta voidaan laajentaa kolmeen tapahtumaan A, B ja C:

P (a∩b∩c) = p (a ja b ja c) = p (a) · p (b│a) · p (c│a∩b)

Ja myös useille tapahtumille, kuten₁, -Lla₂, -Lla₃ Ja enemmän, se voidaan ilmaista seuraavasti:

P (a₁∩ A₂ ∩ A₃… ∩ A_n) = P (a₁-A . P (a₂│A₁-A. P (a₃│A₁∩ A₂) ... P (a_n│A₁∩ A₂∩… a_N-1-A

Kun järjestyksessä ja eri vaiheissa tapahtuvien tapahtumien tapaus on kätevää järjestää tiedot kaaviossa tai taulukossa. Tämä helpottaa visualisoimalla vaihtoehtoja saavuttaakseen pyydetyn todennäköisyyden.

Esimerkkejä tästä ovat puukaavio ja varataulukko. Yhdeltä heistä voit rakentaa toisen.

Esimerkkejä ehdollisesta todennäköisyydestä

Tarkastellaan joitain tilanteita, joissa tapahtuman todennäköisyydet muuttuvat toisen esiintymisellä:

- Esimerkki 1

Makeassa myymälässä myydään kahta tyyppiä kakkuja: mansikka ja suklaa. Kun rekisteröidyt molempien sukupuolten 50 asiakkaan mieltymykset, määritettiin seuraavat arvot:

-27 naista, joista 11 mieluummin mansikka- ja 16 suklaakakkua.

-23 miestä: 15 suklaata ja 8 mansikkaa.

Todennäköisyys, että asiakas valitsee suklaakakun, voidaan määrittää soveltamalla Laplace -sääntöä, jonka mukaan minkä tahansa tapahtuman todennäköisyys on:

P = suotuisten tapahtumien lukumäärä/tapahtumien kokonaismäärä

Tässä tapauksessa 50 asiakkaasta yhteensä 31 mieluummin suklaata, jotta todennäköisyys olisi p = 31/50 = 0.62. Eli 62% asiakkaista mieluummin suklaakakku.

Voi palvella sinua: polynomiyhtälöt

Mutta olisiko se erilaista, jos asiakas on nainen? Tämä on ehdollisen todennäköisyyden tapaus.

Varataulukko

Tämänkaltaisen varautumispöydän kautta kokonaismäärät visualisoidaan helposti:

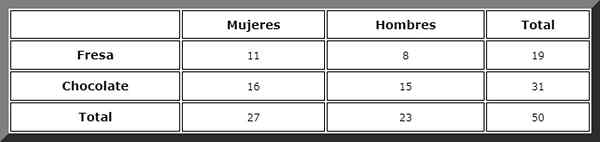
Sitten havaitaan suotuisia tapauksia ja Laplace -sääntöä sovelletaan, mutta ennen kuin määrittelemme tapahtumat:

-B on "Naisten asiakas" -tapahtuma.

-A on tapahtuma "mieluummin suklaakakku" on nainen.

Menemme sarakkeeseen, jossa on "naiset" ja siellä näemme, että kokonaismäärä on 27.

Sitten "suklaan" rivillä haetaan suotuisa tapaus. Näistä on 16 tapahtumaa, joten haluttu todennäköisyys on suoraan:

P (a│b) = 16/27 = 0.5924

A 59.24 % naisista naisista mieluummin suklaakakkua.

Tämä arvo tapahtuu samanaikaisesti, kun olemme vastakohtana ehdollisen todennäköisyyden alun perin annettuun määritelmään:

P (a│b) = p (a∩b) / p (b)

Varmistamme itsemme Laplace -säännön ja taulukon arvojen kautta:

P (b) = 27/50

P (a ja b) = 16/50

Missä p (a ja b) on todennäköisyys, että asiakas suosii suklaata ja on nainen. Nyt arvot korvataan:

P (a│b) = p (a ja b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

Ja on todistettu, että tulos on sama.

- Esimerkki 2

Tässä esimerkissä kerroinsääntöä sovelletaan. Oletetaan.

Paljon, jossa on yhteensä 24 housua, joista jokaista koosta on 8 ja kaikki ovat sekoitettuja. Mikä olisi todennäköisyys purkaa kaksi ja että molemmat olivat pieniä?

On selvää, että pienten housujen purkamisen todennäköisyys ensimmäisessä yrityksessä on 8/24 = 1/3. Nyt toinen uuttaminen on ehdollinen ensimmäiseen tapahtumaan, koska kun otat housut, ei ole enää 24, mutta 23. Ja jos pienet housut poistetaan, niiden sijasta on 7.

Voi palvella sinua: Moninkertainen periaate: Laskentatekniikat ja esimerkit

Tapahtuma A on ottaa pienet housut, kun hän on ottanut toisen ensimmäisessä yrityksessä. Ja tapahtuma B on pienet housut ensimmäiseen. Siksi:

P (b) = 1/3; P (a│b) = 7/24

Lopuksi, kertolaskusääntö:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Liikuntaa

Kaupallisten lentolentojen täsmällisyyden tutkimuksessa seuraavia tietoja on saatavana:

-P (b) = 0.83, on todennäköisyys, että lentokone vie oikea -aikaisen ottamisen.

-P (a) = 0.81, on todennäköisyys laskeutua ajoissa.

-P (b∩a) = 0.78 on todennäköisyys, että lento saapuu ajoissa ottaen oikea -aikaista.

Sitä pyydetään laskemaan:

a) Mikä on todennäköisyys, että kone laskeutuu nopeasti, koska se alkoi ajoissa?

b) Yllä oleva todennäköisyys on sama kuin todennäköisyys, että se on ilmestynyt ajoissa, jos onnistut laskeutumaan nopeasti?

c) ja lopuksi: mikä on todennäköisyys, että se tulee ajoissa, koska se ei tullut ulos ajoissa?

Kuva 2. Kaupallisten lennojen täsmällisyys on tärkeää, koska viivästykset aiheuttavat miljonääriä tappioita. Lähde: Pixabay.

Liittää jhk

Kysymykseen vastaamiseksi käytetään ehdollisen todennäköisyyden määritelmää:

P (a│b) = p (a∩b) / p (b) = p (a ja b) / p (b) = 0.78/0.83 = 0.9398

Ratkaisu b

Tässä tapauksessa tapahtumia vaihdetaan määritelmässä:

P (b│a) = p (a∩b) / p (a) = p (a ja b) / p (a) = 0.78/0.81 = 0.9630

Huomaa, että tämä todennäköisyys on hiukan erilainen kuin edellisestä, kuten aiemmin osoitimme.

Liuos C

Todennäköisyys, että ei ole täsmällistä, on 1 - p (b) = 1 - 0,83 = 0.17, kutsumme sitä p (b^C), Koska täydentävä tapahtuma on oikea -aikainen. Ehdollinen todennäköisyys on:

P (A│B^C) = P (A∩B^C) / P (b^C) = P (a ja b^C)/P (b^C-A

Toisaalta:

P (A∩B^C) = P (aikalasku) - P (aikalasku ja kurkistaminen) = 0.81-0.78 = 0.03

Tässä tapauksessa etsitty todennäköisyys on:

P (A│B^C) = 0.03/0.17 = 0.1765

Viitteet

1. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Lipschutz, S. 1991. Schaum -sarja: todennäköisyys. McGraw Hill.
4. Obregón, minä. 1989.Todennäköisyyden teoria. Toimituslimusa.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.
6. Wikipedia. Ehdollinen todennäköisyys. Palautettu: on.Wikipedia.org.