Teoreettinen todennäköisyys kuinka se saadaan ulos, esimerkkejä, harjoituksia

Se Teoreettinen todennäköisyys (tai Laplace), että tapahtuu tapahtuma, joka kuuluu näytetilaan S, jossa kaikilla tapahtumilla on sama tapahtumatodennäköisyys, se on määritelty matemaattisessa merkinnässä, kuten: p (e) = n (e) / n ( S)

Jos p (e) on todennäköisyys, annetaan suhde E -tapahtuman mahdollisten tulosten kokonaismäärän välillä, jota kutsumme n (e), jaettuna mahdollisten tulosten kokonaismäärällä N (S) näytteen tilassa S.

Kuvio 1. Kuusipuolisen noppaa käynnistäessä teoreettinen todennäköisyys, että kolme pistettä kasvot ovat yläosassa, on ⅙. Lähde: Pixabay.

Teoreettinen todennäköisyys on reaaliluku välillä 0 ja 1, mutta se ilmaistaan ​​usein prosentuaalisena muodossa, jolloin todennäköisyys on arvo välillä 0% - 100%.

Tapahtuman tapahtuman todennäköisyyden laskeminen on erittäin tärkeää monilla aloilla, kuten osakemarkkinoiden toiminta, vakuutusyhtiöt, uhkapelit ja monet muut.

[TOC]

Kuinka saada teoreettinen todennäköisyys?

Havainnollistava tapaus on rifas tai arpajaiset. Oletetaan, että 1.000 lippua rifarille älypuhelimelle. Koska arpajainen tehdään satunnaisesti, jollain lippuista on samat mahdollisuudet olla voittaja. 

Löytääksesi todennäköisyyden, että henkilö, joka ostaa lipun numerolla 81, on voittaja, seuraava laskelma Teoreettinen todennäköisyys-

P (1) = 1/1.000 = 0,001 = 0,1%

Aikaisempi tulos tulkitaan seuraavasti: Jos arpajainen toistetaan äärettömästi, joka 1.000 kertaa lippu 81 valitaan keskimäärin kerran.

Jos jostain syystä joku hankkii kaikki liput, on varma, että hän voittaa palkinnon. Palkinnon voittamisen todennäköisyys, jos kaikki liput on laskettu seuraavasti:

Se voi palvella sinua: ympyrän kehä: Kuinka ottaa se pois ja kaavat, ratkaistut harjoitukset

P (1.000) = 1.000/1.000 = 1 = 100%.

Eli mikä todennäköisyys 1 tai 100% tarkoittaa, että on täysin varma, että tämä tulos tapahtuu.

Jos jollakin on 500 lippua, voiton tai häviämisen mahdollisuudet ovat samat. Palkinnon voittamisen teoreettinen todennäköisyys tässä tapauksessa lasketaan seuraavasti:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Hänellä, joka ei osta lippua, ei ole mahdollisuutta voittaa, ja hänen teoreettinen todennäköisyys on määritetty näin:

 P (0) = 0 /1.000 = 0 = 0%

Esimerkit

Esimerkki 1

Sinulla on valuutta kallis toisella puolella ja kilpi tai sulje toiseen. Kun valuutta käynnistetään, mikä on teoreettinen todennäköisyys olla kallis?

P (kallis) = n (kallis) / N ( kasvot + kilpi ) = ½ = 0,5 = 50%

Tulos tulkitaan seuraavasti: Jos tehdään valtava määrä julkaisuja, keskimäärin jokaisessa kahdessa paikassa, joista yksi niistä kohtaa.

Prosentteina tulkinta on tulkinta, että loputtoman suuren määrän laukaisujen tekeminen keskimäärin jokainen 100 niistä 50 johtaisi kalliisiin.

Esimerkki 2

Laatikossa on 3 sinistä marmoria, 2 punaista marmoria ja 1 vihreää. Mikä on teoreettinen todennäköisyys, että kun saat marmorin laatikosta, tämä on punainen?

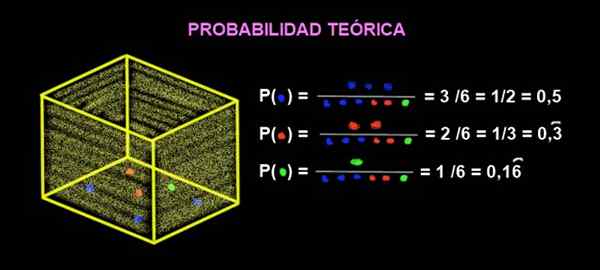Kuva 2. Värimarmorien uuttamisen todennäköisyys. Lähde: f. Zapata.

Punainen todennäköisyys on:

P (punainen) = suotuisten tapausten lukumäärä / mahdollisten tapausten lukumäärä

Tarkoittaen:

P (punainen) = punaisten marmorien lukumäärä / marmorien kokonaismäärä

Lopuksi todennäköisyys, että punainen marmori on:

P (punainen) = 2/6 = ⅓ = 0,3333 = 33,33%

Vaikka todennäköisyys, että vihreän marmorin purkaminen on:

P (vihreä) = ⅙ = 0,1666 = 16,66%

Lopuksi, teoreettinen todennäköisyys saada sokeaan uuttoon sininen marmori on: 

P (sininen) = 3/6 = ½ = 0,5 = 50%

Se voi palvella sinua: radikaalit ominaisuudet

Toisin sanoen jokaisesta kahdesta yrityksestä tulos on sininen yhdessä niistä ja toinen väri toisessa yrityksessä, oletuksella, että uutettu marmori on täydennetty ja että kokeiden lukumäärä on erittäin, erittäin suuri.

Harjoitukset

Harjoitus 1

Määritä todennäköisyys, että noppaa käynnistettäessä arvo saadaan vähemmän tai yhtä suuri kuin 4.

Ratkaisu

Tämän tapahtuman todennäköisyyden laskemiseksi sovelletaan teoreettisen todennäköisyyden määritelmää:

P (≤4) = suotuisten tapausten lukumäärä / mahdollisten tapausten lukumäärä

P (≤5) = 5/6 = = 83,33%

Harjoitus 2

Löydä todennäköisyys, että kahdessa peräkkäisessä kentässä normaalin kuusipuolisen noppan, 2 kertaa 2 kertaa.

Ratkaisu

Tähän harjoitukseen reagointia on kätevää tehdä kuva kaikkien mahdollisuuksien näyttämiseksi. Ensimmäinen luku osoittaa ensimmäisen noppan tuloksen ja toisen tuloksen toisen.

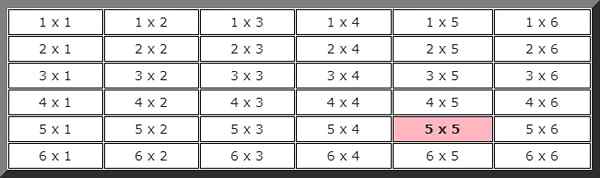
Teoreettisen todennäköisyyden laskemiseksi meidän on tiedettävä mahdollisten tapausten kokonaismäärä, tässä tapauksessa, kuten edellisestä taulukosta voidaan nähdä, mahdollisuuksia on 36.

Tarkkailemalla myös maalausta seuraa, että tapahtuman kannalta suotuisten tapausten lukumäärä on, että kahdessa peräkkäisessä julkaisussa tulee vain 5, joka on korostettu värillä, joten todennäköisyys, että tämä tapahtuma tapahtuu, on:

P (5 x 5) = 1/33.

Tämä tulos olisi voinut saavuttaa myös käyttämällä yhtä teoreettisen todennäköisyyden ominaisuuksia, joiden mukaan kahden riippumattoman tapahtuman yhdistetty todennäköisyys on heidän yksittäisten todennäköisyyksiensä tuote.

Tässä tapauksessa todennäköisyys, että ensimmäisessä julkaisussa 5 on ⅙. Toinen lanseeraus on täysin riippumaton ensimmäisestä, joten todennäköisyys, että 5 toisessa on myös ⅙. Joten yhdistetty todennäköisyys on:

Voi palvella sinua: Osittaiset johdannaiset: Ominaisuudet, laskelmat, harjoitukset

P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.

Harjoitus 3

Löydä todennäköisyys, että alle 2 -luku tulee esiin ensimmäisessä käynnistyksessä ja toisessa lukumäärä yli 2 tulee ulos. 

Ratkaisu

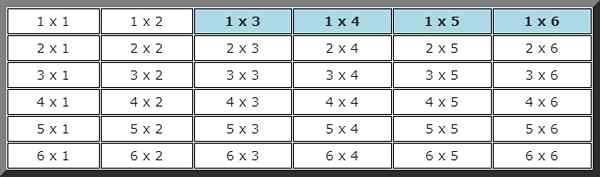
Jälleen sinun on rakennettava mahdollinen tapahtumapöytä, jossa ne, joissa ensimmäinen lanseeraus oli alle 2 ja toisessa yli 2: n aikana korostetaan.

Kaikkiaan on 4 mahdollisuutta yhteensä 36. Toisin sanoen tämän tapahtuman todennäköisyys on:

P (2) = 4/36 = 1/9 = 0,1111 = 11,11%

Käyttämällä todennäköisyyslausetta, jossa todetaan:

Kahden riippumattoman tapahtuman esiintymisen todennäköisyys on yhtä suuri kuin yksittäisten todennäköisyyksien tuote.

Se saa identtinen tulos:

P (2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%

Tällä menetelmällä saatu arvo osuu edellisen tuloksen kanssa, teoreettisen tai klassisen määritelmän kautta todennäköisyyden avulla.

Harjoitus 4

Mikä on todennäköisyys, että käynnistämällä kaksi arvojen summa on 7.

Ratkaisu

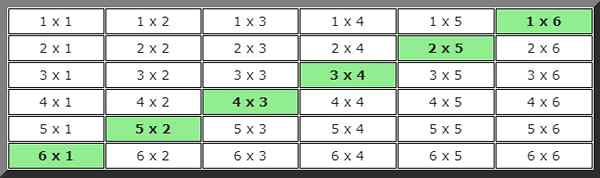
Ratkaisun löytämiseksi tässä tapauksessa on kehitetty kuva mahdollisuuksista, joissa arvojen ehtoa täyttävät tapaukset on merkitty värillisesti.

Taulukkoa tarkasteltaessa 6 mahdollista tapausta voidaan laskea, joten todennäköisyys on:

P (R & D II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Viitteet

1. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Lipschutz, S. 1991. Schaum -sarja: todennäköisyys. McGraw Hill.
4. Obregón, minä. 1989.Todennäköisyyden teoria. Toimituslimusa.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.