Mikä on hiukkasen tasapaino? (Esimerkkejä)

Hän hiukkasten tasapaino Se on tila, jossa hiukkas on silloin, kun niihin vaikuttavat ulkoiset voimat kumotaan toistensa kanssa. Tämä tarkoittaa, että se ylläpitää jatkuvaa tilaa, jotta se voi tapahtua kahdella eri tavalla erityisestä tilanteesta riippuen.

Ensimmäinen on olla staattisessa tasapainossa, jossa hiukkas on liikkumaton; Ja toinen on dynaaminen tasapaino, jossa voimien summa peruutetaan, mutta silti hiukkasella on tasainen välikerros.

Kuvio 1. Tasapainottaa kallion muodostumista. Lähde: Pixabay.

Hiukkasmalli on erittäin hyödyllinen lähestymistapa kehon liikkeen tutkimiseen. Se koostuu olettamisesta, että koko kehon massa on keskittynyt yhteen pisteeseen, objektin koosta riippumatta. Tällä tavalla voit edustaa planeettaa, autoa, elektronia tai biljardipalloa.

[TOC]

Tuloksena oleva voima

Kohdetta edustavassa kohdassa siihen vaikuttavat voimat. Kaikki nämä voimat voidaan korvata yhdellä, joka tekee saman vaikutuksen, jota kutsutaan tuloksena oleva voima jompikumpi Nettovoima Ja se on merkitty f: ksi_{R -} tai f_N.

Newtonin toisen lain mukaan, kun tuloksena on epätasapainossa, keho kokee kiihtyvyyden suhteessa voimaan:

F_{R -} = m.-lla

Missä -lla Seceleration, jonka esine hankkii voiman vaikutuksen ansiosta, ja m Se on esineen massa. Mitä tapahtuu, jos vartaloa ei kiihdytetä? Juuri mitä alussa osoitettiin: Runko on levossa tai liikkuu yhtenäisellä välittömällä liikkuvuudella, josta puuttuu kiihtyvyys.

Tasapainossa olevalle hiukkaselle on pätevä varmistaa, että:

F_{R -} = 0

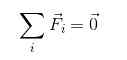
Koska vektorien lisääminen ei välttämättä tarkoita moduuleja, vektorien on hajotettava. Siten on pätevä ilmaista:

F_x = m.-lla_x = 0; F_ja = m.-lla_ja = 0; F_{z -z} = m.-lla_{z -z} = 0

Vapaat kehon kaaviot

Hiukkasen kanssa toimivien voimien visualisoimiseksi tulisi tehdä vapaan kehon kaavio, jossa kaikki esineeseen vaikuttavat voimat edustavat nuolet.

Voi palvella sinua: Maan magnetosfääri: Ominaisuudet, rakenne, kaasut

Aikaisemmat yhtälöt ovat vektorien luonne. Hajottamalla voimat, ne erottuvat merkkeistä. Tällä tavalla on mahdollista, että sen komponenttien summa on nolla.

Seuraavat ovat tärkeitä merkinnät piirustukselle hyödyllisiksi:

- Valitse referenssijärjestelmä, jossa suurin osa voimista sijaitsee koordinaattiakseleilla.

- Paino vedetään aina pystysuoraan.

- Kaksi tai useampaa kosketuksessa olevaa olemassa olevaa olemassa olevaa olemassa olevaa normaalia voimaa, jotka aina piirretään työntämällä vartalo ja kohtisuorassa sitä käyttävään pintaan nähden.

- Tasapainon hiukkaselle voi olla kitka kosketuspinnan suuntainen ja mahdollisen liikkeen vastustaminen, jos hiukkasia pidetään levossa tai ehdottomasti vastustuksessa, jos hiukkanen liikkuu MRU: lla (tasainen suorasunkolainen liike).

- Jos on köyttä, jännitys vedetään aina sitä pitkin ja vetämällä vartaloa.

Tapoja soveltaa tasapainoolosuhteita

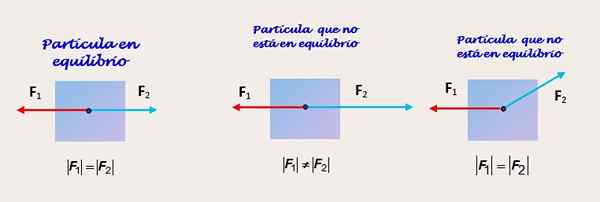
Kuva 2. Kaksi levitettyä voimaa eri tavoin samassa ruumiissa. Lähde: Itse tehty.

Kaksi yhtä suurta ja suuntaa ja vastakkaisia ​​aisteja

Kuvio 2 esittää hiukkasen, jolla kaksi voimaa toimii. Vasemmalla olevassa kuviossa hiukkas saa kahden voiman f: n vaikutuksen f₁ ja f₂ joilla on sama suuruus ja toimivat samaan suuntaan ja vastakkaisiin aisteihin.

Hiukkas on tasapainossa, mutta silti tiedon kanssa, jos ei ole mahdollista tietää, onko saldo staattinen vai dynaaminen. Tarvitaan lisätietoja inertiaalisesta referenssijärjestelmästä, josta objektia havaitaan.

Kaksi erilaista voimaa, yhtä suuri suunta ja vastakkaiset aistit

Keskikuvio näyttää saman hiukkasen, joka tällä kertaa ei ole tasapainossa, koska voiman F suuruus₂ on suurempi kuin F₁. Siksi on epätasapainoinen voima ja esineellä on kiihtyvyys samaan suuntaan kuin F₂.

Voi palvella sinua: Darcy Law

Kaksi yhtä suurta ja eri suuntaa

Lopuksi oikealla olevassa kuvassa havaitsemme ruumiin, joka ei ole myöskään tasapainossa. Vaikka f₁ ja f₂ Heillä on sama suuruus, voima f₂ Se ei ole samaan suuntaan kuin 1. F: n pystysuuntainen komponentti₂ Mikään muu ei ole torjunta, ja hiukkaset kokevat kiihtyvyyden siihen suuntaan.

Kolme voimaa eri suuntaan

Voidaanko kolmen voiman toimitettu hiukkanen olla tasapainossa? Kyllä, niin kauan kuin kunkin kärjessä asettaessa, tuloksena oleva luku on kolmio. Tässä tapauksessa vektorisumma on tyhjä.

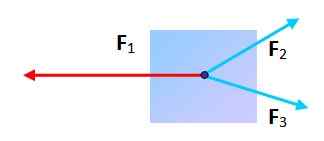Kuva 3. Kolmen voiman vaikutuksesta alainen hiukkas voi olla tasapainossa. Lähde: Itse tehty.

Kitka

Voima, joka puuttuu usein hiukkasten tasapainoon, on staattinen kitka. Se johtuu hiukkasen edustaman esineen vuorovaikutuksesta toisen pinnan kanssa. Esimerkiksi kaltevan taulukon staattisen tasapainon kirja on mallinnettu hiukkaseksi ja siinä on vapaa kehon kaavio, kuten seuraava:

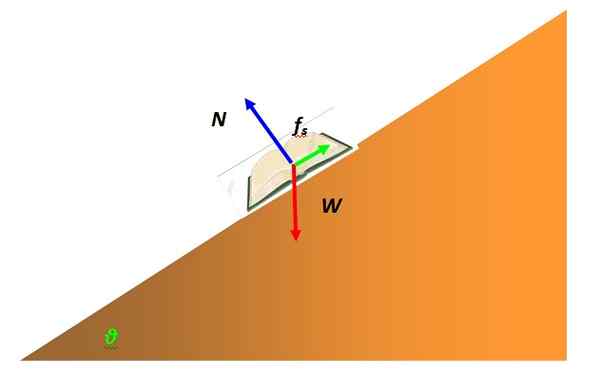Kuva 4. Ilmainen kehon kaavio kirjasta kaltevalla tasolla. Lähde: Itse tehty.

Voima, joka estää kirjaa liukumasta kaltevan tason pinnan läpi ja pysyy levossa, on staattinen kitka. Se riippuu kosketuksessa olevien pintojen luonteesta, joilla mikroskooppisesti on karheus lukittujen piikkien kanssa, estäen liikettä.

Suurin staattinen kitka -arvo on verrannollinen normaaliin voimaan, joka käyttää pintaa tuetulle esineelle, mutta kohtisuorassa mainittuun pintaan nähden. Kirjan esimerkissä on merkitty sinisellä. Matemaattisesti se ilmaistaan ​​seuraavasti:

F_lisää∝ N

Suhteellisuusvakio on Staattinen kitkakerroin μ_s, joka määritetään kokeellisesti, on ulottumaton ja riippuu kosketuksessa olevien pintojen luonteesta.

F_{S max} = μ_s N

Dynaaminen kitka

Jos hiukkanen on dynaamisessa tasapainossa, liike tapahtuu jo ja staattinen kitka ei puutu enemmän. Jos jonkin verran liikettä vastustavat kitkavoimat ovat läsnä, dynaaminen kitka, jonka voimakkuus on vakio ja antanut:

Voi palvella sinua: mitkä ovat lämpöominaisuudet ja mitkä ovat? (Esimerkkejä)

F_{k -k -} = μ_{k -k -} N

Missä μ_{k -k -} onko hän dynaaminen kitkakerroin, joka riippuu myös kosketuksessa olevien pintojen tyypistä. Kuten staattinen kitkakerroin, se on ulottumaton ja sen arvo määritetään kokeellisesti.

Dynaamisen kitkakertoimen arvo on yleensä pienempi kuin staattisen hankauksen arvo.

Ratkaistu esimerkki

Kuvan 3 kirja on levossa ja sen massa on 1.30 kg. Tason kaltevuuskulma on 30º. Etsi kirjan ja tason pinnan välillä staattinen kitkakerroin.

Ratkaisu

On tärkeää valita sopiva referenssijärjestelmä, katso seuraava kuva:

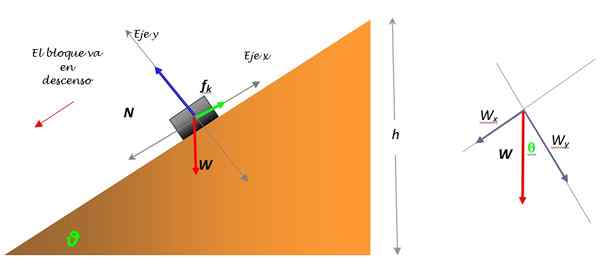Kuva 5. Kirja -vapaa rungon kaavio kaltevassa tasossa ja painon hajoamisessa. Lähde: Itse tehty.

Kirjan paino on suuruusluokka W = mg, On kuitenkin tarpeen hajottaa se kahteen komponenttiin: W -_x ja W -_ja, Koska se on ainoa voima, joka ei laske vain minkään koordinaattiakselin yläpuolelle. Painon hajoaminen havaitaan vasemmalla olevassa kuvassa.

W -_ja = mg.cosθ = 1.30 x 9.8 x cos 30º N = 11.03 n

W -_x = mg.Sentr = 1.30 x 9.8 x Sen 30º = 6.37 n

Toinen. Newtonin laki pystysuoralle akselille on:

N - wy = 0

N = mg. cos θ = 11.03 n.

2. päivä. Newtonin X -akselin laki, valitsemalla positiivinen mahdollisen liikkeen suunnan:

W -_x - F_s = 0

Suurin kitka on F_{s max}= μ_sN, siksi:

W -_x - μ_sN = 0

μ_s = W_x / N = 6.37/11.03 = 0.58

Viitteet

1. Rex, a. 2011. Fysiikan perusteet. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7^mehu. Ed. Cengage -oppiminen. 120 - 124.
3. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Ed. Cengage -oppiminen. 99-112.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fysiikka. Addison Wesley. 148-164.