Mikä on magneettinen hetki?

Hän Magneettinen hetki Se on vektori, joka yhdistää virran, joka ylittää hiukan tai suljetun silmukan saman alueen kanssa. Sen moduuli on yhtä suuri kuin virran voimakkuuden tuote alueen mukaan, ja sen suunta ja suunta annetaan oikeanpuoleisella sääntöllä, kuten kuvassa 1 esitetään.

Tämä määritelmä on voimassa riippumatta. Mitä tulee magneettisen hetken yhtenäisyyteen, kansainvälisessä yksikköjärjestelmässä, jos se on ampeeri × M².

Kuvio 1. Mielivaltaisen virran sidoksen magneettinen momenttivektori on kohtisuorassa sen tasoon nähden ja suunta määritetään oikean peukalon säännön perusteella. Lähde: Wikimedia Commons.

Matemaattisesti, vektorimagneettisen momentin merkitseminen kreikkalaisten lyricsin kanssa μ (Boldissa, koska se on vektori ja erottuu siten sen suuruudesta), se ilmaistaan ​​seuraavasti:

μ = Ia n

Missä olen virran voimakkuus, A on alue, joka sulkee silmukan ja n Juuri yksikkövektori (moduulista yhtä suuri kuin 1) osoittaa spaasin tasoon kohtisuorassa olevaan suuntaan ja jonka merkitys annetaan oikean peukalon sääntöllä (katso kuva 1).

Tämä sääntö on hyvin yksinkertainen: oikean käden neljä sormea ​​niin, että ne seuraavat virtaa, peukalo osoittaa suuntaa ja suuntaa n ja siksi magneettinen hetki.

Aikaisempi yhtälö on voimassa silmukassa. Jos kelassa on nougasia, magneettinen momentti kerrotaan n:

μ = nIa n

[TOC]

Magneettinen momentti ja magneettikenttä

On helppo löytää lausekkeita käännösmagneettiselle momentille tavallisilla geometrisilla muodoilla:

-Sivun neliöpuoli ℓ: μ = Iℓ² n

-Sivujen suorakaiteen muotoinen spiraali -lla ja b -- μ = Iab n

-Radio R. Radio Spira: μ = Iπr² n

Voi palvella sinua: Atominumero

Dipolon magneettikenttä

Nykyisen silmukan tai spaasin tuottama magneettikenttä muistuttaa palkkimagneetin ja myös maan kentästä.

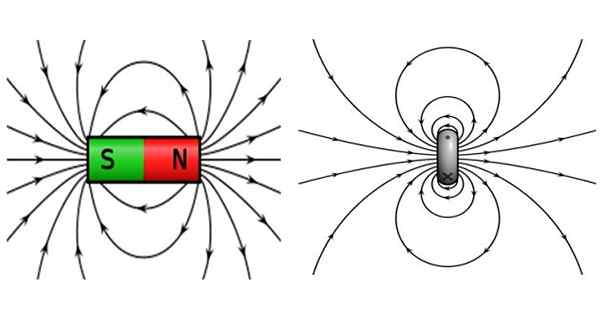Kuva 2. Vasemmalta palkkamagneetin magneettikenttä ja oikealle, joka tuottaa pyöreän spiraalin, joka kuljettaa virtaa. Lähde: Wikimedia Commons.

Baarimagneeteille on ominaista pohjoisnapa ja eteläinen napa, missä vastakkaiset pylväät houkuttelevat ja samat puolalaiset hylkivät. Kenttäviivat ovat kiinni, jätä pohjoisnapa ja saavuta etelänapa.

Nyt magneettiset pylväät ovat erottamattomia, mikä tarkoittaa, että jos baarimagneetti on jaettu kahteen pienempään magneettiin, niillä on edelleen omat pohjoisen ja eteläisen navansa. Eristettyjä magneettisia napoja ei ole mahdollista, minkä vuoksi palkkimagneetti kutsutaan Magneettinen dipolo.

Virta I: n kuljettavan säteen R-spiraalin magneettikenttä lasketaan biot-savalalla. Sen symmetria -akselille (tässä tapauksessa X -akseli) kohdalla oleville pisteille kenttä on annettu:

Missä μ_jompikumpi Se on tyhjiön läpäisevyys. Pellon poistuminen pisteistä, jolle kenttä lähestyy:

Magneettikentän ja dipolon magneettisen momentin välinen suhde

Sisältää magneettisen momentin edellisessä lausekkeessa on:

Tällä tavalla magneettikentän voimakkuus on verrannollinen magneettiseen hetkeen. Huomaa, että kentän intensiteetti vähenee etäisyyskuutiolla.

Tätä lähestymistapaa voidaan soveltaa mihin tahansa silmukkaan, niin kauan kuin x olla suuri verrattuna sen ulottuvuuksiin.

Ja kun tämän kentän viivat muistuttavat palkkimagneetin linjoja, yhtälö on hyvä malli tälle magneettikentälle ja muiden järjestelmien, joiden viivat ovat samanlaisia, kuten: esimerkiksi: esimerkiksi:

Voi palvella sinua: absorbanssi: Mikä on, esimerkit ja harjoitukset ratkaistu

-Hiukkaset ladattu elektroniksi.

-Atomi.

-Maa- ja muut aurinkokunnan planeetat ja satelliitit.

-Tähdet.

Ulkoisen kentän vaikutus silmukkaan

Erittäin tärkeä magneettisen momentin ominaisuus on sen yhteys vääntömomenttiin, jonka silmukkakokemus ulkoisen magneettikentän läsnä ollessa.

Sähkömoottori sisältää kelat, joiden läpi muuttuvan suunnan virtaus on läpi ja että ulkoisen kenttäkokemuksen ansiosta käännösvaikutus. Tämä käännös saa akselin liikkumaan ja sähköenergiasta tulee mekaaninen energia prosessin aikana.

Vääntömomentti suorakaiteen muotoisessa silmukassa

Oletetaan, että laskelmien helpottamiseksi suorakulmaiset sivut -lla ja b -, Kenen normaali vektori n, Lähtevä näyttö, alun perin se on kohtisuorassa tasaisen magneettikentän kanssa B -, kuten kuvassa 3. Silmukkakokemuksen puolet antavat:

F = ILens x B -

Missä Lens Se on suuruusvektori, joka on yhtä suuri kuin segmentin pituus ja ohjataan virran mukaan, ja se on saman intensiteetti ja B - Se on kenttä. Voima on kohtisuorassa molemmille Lens Kuten kenttä, mutta ei kaikki osapuolet kokevat voimaa.

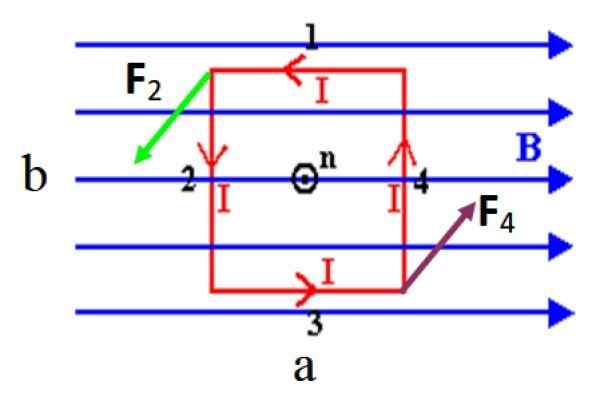Kuva 3. Suorakulmainen spiraali, joka kuljettaa virran I: n anti -horary -mielessä, kokee vääntömomentin tasaisen tasaisen magneettikentän läsnä ollessa. Lähde: f. Zapata.

Esitetyssä kuvassa ei ole lujuutta lyhyillä sivuilla 1 ja 3 kentän suuntaisesti, muista, että rinnakkaisvektoreiden välinen ristituote on mitätön. Pitkät sivut 2 ja 4, jotka ovat kohtisuorassa B -, He kokevat merkittyjä joukkoja F₂ ja F₄.

Nämä voimat muodostavat pari: Niillä on sama suuruus ja suunta, mutta vastakkaiset aistit, siksi he eivät pysty liikkumaan silmukkaan kentän keskellä. Mutta ne voivat saada sen kiertämään, koska vääntömomentti  τ Että jokainen voima käyttää suhteessa pystysuuntaiseen akseliin, joka kulkee silmukan keskustan läpi, sillä on sama suunta ja merkitys.

Voi palvella sinua: Yhteysvoima

Vääntömomentin määritelmän mukaan missä r - Se on sijaintivektori:

τ = r - x F

Niin:

τ₂ = τ₄=(A/2) F (+J - -A

Yksittäisiä vääntömomentteja ei peruuteta, koska niillä on sama suunta ja merkitys, niin ne lisätään:

τ_netto = τ₂ + τ₄ = f (+J - -A

Ja koska se on voiman F = IBB, se johtaa:

τ_netto = I⋅a⋅b⋅b (+J - -A

A⋅B -tuote on spaasin alue A, joten IAB on magneettisen momentin suuruus μ. Siksi τ_netto = μ⋅B (+J - -A

Voidaan nähdä, että yleensä vääntömomentti osuu vektorituotteen kanssa vektorien välillä μ ja B --

τ_netto = μ x B -

Ja vaikka tämä lauseke on johdettu suorakaiteen muotoisesta silmukasta, se pätee litteään jalansijaan mielivaltaisesti.

Kentän vaikutus silmukkaan on vääntömomentti, jolla on taipumus kohdistaa magneettinen momentti kentän kanssa.

Magneettisen dipolin potentiaalienergia

Spiraalin tai dipolin kääntämiseksi kentän keskellä on tehtävä työ, joka muuttaa Dipolon potentiaalista energiaa. Energian ΔU variaatio, kun spiraali pyörii kulmasta θ_jompikumpi Kulmassa θ annetaan integraali:

Jos vertailutaso valitaan θ_jompikumpi = π/2:

Δu = -μb cos θ

Joka puolestaan ​​voidaan ilmaista skalaarituotteena vektorien välillä B - ja μ-

ΔU = - μ ·B -

Dipolin vähimmäispotentiaalienergia tapahtuu, kun cos θ = 1, mikä tarkoittaa sitä μ ja B - Ne ovat yhdensuuntaisia, energia on maksimiarvo, jos ne ovat päinvastaisia ​​(θ = π) ja ovat nolla, kun ne ovat kohtisuorassa (θ = π/2).

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
2. Resnick, r. 1999. Fyysinen. Osa. 2. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 2. Pearson.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Nide 2. Seitsemäs. Ed. Cengage -oppiminen.
5. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Nide 2. Toimitus palautti.