Mikä on ohje? (Geometria)

Se direktiivi Geometriassa se koostuu käyrästä, pinnasta tai tilavuudesta, joka pysyy kiinteänä ja määrittää tapaa, jolla geometrinen objekti muodostuu. Esimerkiksi linjalla muut käyrät, kuten kartiomaiset ja vallankumouspinnat, kuten suora pyöreä sylinteri.

Ohjekäyrä voi olla myös kehä. Suora pyöreä sylinteri voidaan muodostaa jättämällä säde ri -r rión ri.

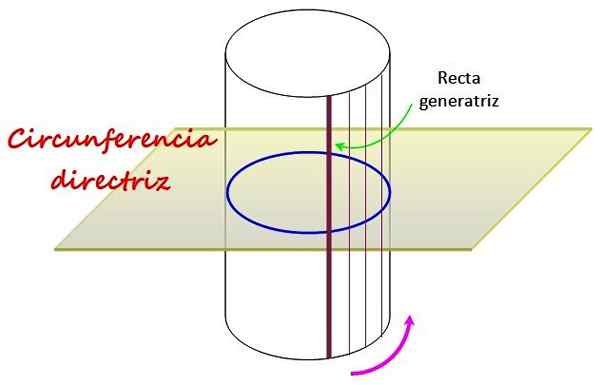
Kuvio 1. Suora pyöreällä sylinterillä on opas ympyrä, jonka ympärillä on suora viiva, jota kutsutaan generatrix -liikkeiksi. Lähde: f. Zapata.

Kuvassa vedettyyn tason ympärysmitta määrittää suoran pyöreän sylinterin kaarevan pinnan muodon, joka syntyy kiertämällä sen ympärillä olevaa linjaa, jota kutsutaan suoran generatrix.

Jos ohjauskäyrä ei ole kehä, vaan toinen käyrä, syntyy muun tyyppisiä sylinteriä, kuten elliptinen sylinteri, jonka ohje on ellipsi.

Ympäristö voi myös toimia ohjeena toisen käyrän luomiseksi Epitrokoidi, Käyrä pisteen tuottamassa tasossa, joka puolestaan ​​on pienemmässä ympyrässä, joka rullaa liukua, ohjeen ympärillä.

Seuraavan animaation avulla sitä on helpompi arvioida sitä visuaalisesti:

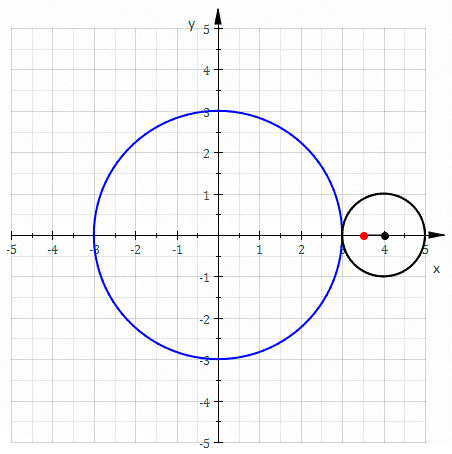Kuva 2. Punainen käyrä kutsutaan Epetrocide ja sen ohjekäyrä. Lähde: Wikimedia Commons. Sam Derbyshire englanniksi Wikipedia/CC BY-S (http: // creativecommons.Org/lisenssit/by-SA/3.0/).

Sylinterimäisten pintojen ohjekäyrä

Sylinterimäiset pinnat luokitellaan sylinterien ohjekäyrän mukaan:

-Pyöreä

-Elliptinen

-Parabolinen

-Hyperbolinen

Kun lieriömäisellä pinnalla on suuntaviiva, joka sijaitsee kohtisuorassa tasossa generatrix -viivan tasoon, mainitun pinnan yhtälö on sama kuin ohjeen ohjeet.

Se voi palvella sinua: mikä on Rhombus -alueen ja suorakulmion välinen suhde?

Sylinterit kuuluvat ryhmään Nelipinnat, jonka yhtälö on toinen luokka kolmella muuttujalla. Yleinen muoto on:

Kirves² + Ohella² + Cz² + Dxy + exz + fyz + gx + hy + iz + k = 0

Missä kertoimet A, B, C ... ovat todellisia lukuja.

Sylinterit ovat yleisimpiä ja hyödyllisiä kolmiulotteisia geometrisia kappaleita, joita löytyy.

Suora pyöreä sylinteri

Sen suuntaviiva on ympyrä C, joka on sylinteriin kohtisuorassa olevassa tasossa, kuten kuvassa 1 esitetään, koska generatrix -viiva, joka kulkee C: hen sivuttaisen pinnan muodostamiseksi, on kohtisuorassa C.

Alkuperäiseen (0,0) ympärysmitta C -yhtälö C -tasolla on:

x² + ja² = R²

Missä r, kehän säde on selvästi sylinterin säde. Sylinterin korkeus H ulottuu z -akselia pitkin, kohtisuorassa XY -tasossa.

Elliptinen sylinteri

Ohje on ellipsi XY -tasossa, joka on keskittynyt alkuperään (0,0), jonka yhtälö on:

Generatrix on linja, joka on kohtisuorassa XY -tasossa, joka liikkuu ellipsin ympärillä, jotta ne saavat sivua. Ellipsi voi olla missä tahansa korkeudessa Z XY -tasossa.

Esimerkiksi yhtälö ellipsi:

4x² + 9y² = 36

Se on ohjekäyrä, joka aiheuttaa elliptisen sylinterin, jonka yhtälö on 4x² + 9y² = 36, plus z = 0. Lisäämällä tämän viimeisen lausekkeen, on selvää, että se on pinta.

Voi palvella sinua: näytteenottovirhe: kaavat ja yhtälöt, laskenta, esimerkit

Parabolinen sylinteri

Tässä tapauksessa ohje on vertaus, joka voi olla muodoltaan y = x². Siten sylinteri on suunnattu Z -akselia pitkin ja muodostaa vertauksia kärjellä (0,0) kyseistä akselia pitkin.

Parabolisella sylinterillä on levitys aurinkoenergiassa, koska joillakin keräilijöillä on peilit tällä tavalla, jonka läpi auringonvalo on keskittynyt keskittymään. Tämä kohta kulkee suoran putken, jossa öljy saavuttaa lämpötilojen enintään 400 º C.

Hyperbolinen sylinteri

Hyperbolisessa sylinterissä ohjeiden yhtälö on alkuperään keskittynyt hyperbola:

Sylinteri muodostuu pinoon.

Vallankumouspinta

Vallankumouksen pinnan ohjekäyrä on sama vallankumouksen akseli, linja, jonka ympärillä käyrä, joka on vastuussa pinnan luomisesta.

Kierrättävällä käyrällä voi olla mielivaltainen muoto, tällä tavalla alue syntyy tässä animaatiossa:

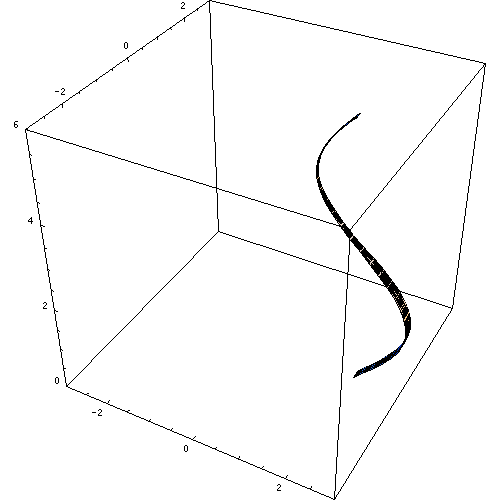Kuva 3. Vallankumouksen pinta. Lähde: Wikimedia Commons. https: // Lataa.Wikimedia.Org/wikipedia/commons/e/e7/rotationskoerper_animation.Gif.

Jos toinen linja käännetään ohjeen ympäri, jo saadaan jo tuttu suora pyöreä sylinteri. Samoin voidaan saada muita vallankumouspintoja, kuten kartiomaisia, pallomaisia ​​ja toroidisia vallankumouspintoja.

Kartiopinta

Kartiomainen pinta syntyy siirtämällä generatrix -viivaa, joka kulkee aina kiinteän litteän käyrän tai ohjekäyrän läpi, ja kiinteällä pisteellä, nimeltään Vertex, joka ei kuulu ohjeasoon.

Voi palvella sinua: matemaattinen toivo: kaava, ominaisuudet, esimerkit, liikunta

Kärki tai kärki jakaa kartion kahteen osaan, nimeltään jättää jompikumpi oksat.

Ratkaisut

- Harjoitus 1

Löydä korkeuden korkean pyöreän sylinterin sivupinta.

Ratkaisu

Sylinterin sivupintainen alue on ohjeen pituuden tuote korkeuden mukaan. Jos R on kehän säde ja H on sylinterin korkeus, alue annetaan:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Harjoitus 2

Sinulla on seuraava yhtälö, joka vastaa nelinkertaista pintaa:

x² + ja² + 2Z² +2xz - 2yz = 1

Ilmoita mikä pinta se on ja mikä on ohjeen yhtälö.

Ratkaisu

Tekemällä z = k, missä k on vakio, se saadaan:

x² + ja² + 2K² +2kx - 2ky = 1

Järjestämme ehdot seuraavasti:

(x² + 2kx) + (ja²- 2Ky) = 1-2K²

Neliöiden on², Jotta ketään suluista ei muuttaisi:

(x² + 2kx + k² - k -k -² ) + (ja² - 2ky + k² - k -k -²) = 1-2K²

(x² + 2kx + k²) - k²  + (ja²- 2ky + k²) - k² = 1-2k²

Tällä tavalla se on edelleen:

(x + k)² + (ja - k)² = 1

Kuten keskiympyrän (-K, K) ja säteen 1 yhtälö, pinta on suora pyöreä sylinteri, myös radio 1, kunhan generatrix-viiva on kohtisuorassa mainittuun kehäyn nähden.

Esimerkiksi K = 0: n tekemällä yhtälö pelkistetään kehokseen, joka keskittyy alkuperään (0,0), jonka säde on 1:

x² + ja² = 1

Viitteet

1. Gaussians. Edustavat kolmen dimensioisia pintoja. Toipunut: Gaussians.com.
2. Kindle, J. Analyyttisen geometrian teoria ja ongelmat. McGraw Hill. Schaum -sarja.
3. Pinnat geometrisinä paikoina. Toipunut: Algebra.Frlp.Utn.Edu.AR.
4. Suárez, m. Pinnat. Haettu: Aiheet.UN -Q.Edu.AR.
5. Nelipinnat. Palautettu: Järjestelmät.fciencias.Yksinäinen.MX.