Mikä on kapasitiivinen reaktanssi ja miten se lasketaan?

Se kapasitiivinen reaktanssi Se on resistanssi, että lauhdutin, kuormitusvirtauksen säätelyelementti vuorottelevassa virtapiirissä, vastustaa virran kulkua.

Lauhduttimesta muodostetussa piirissä, joka aktivoi vuorotteleva virran lähde, kapasitiivinen reaktanssi X voidaan määritellä_C seuraavasti:

X_C = 1 / ωc

Kuvio 1. Kapasitiiviset reaktions. Lähde: Pixabay.

Tai myös:

X_C = 1 / 2πfc

Missä C on kondensaattorin kapasiteetti ja ω on lähteen kulmataajuus, joka liittyy taajuuteen f läpi:

Ω = 2πf

Kapasitiivinen reaktanssi riippuu taajuuden käänteisestä, siksi korkeilla taajuuksilla on taipumus olla pieniä, kun taas matalilla taajuuksilla reaktanssi on suuri.

Kansainvälinen järjestelmäyksikkö kapasitiivisen reaktanssin mittaamiseksi on ohmi (ω), edellyttäen, että kondensaattorin kapasiteetti on Faradissa (lyhennetty F) ja taajuus ilmaistaan ​​sekuntien käänteessä (S S (S^-1-A.

Kun kuorma kestää, jännitteet ja virta perustetaan myös kondensaattorin kautta, jonka suurin amplitudit tai arvot merkitään vastaavasti V: ksi_C ja minä_C, Ne liittyvät kapasitiivisella reaktanssilla, joka on analoginen Ohmin lain kanssa:

V_C = I_C ⋅ x_C

Lauhduttimessa jännite viivästyy 90º virran suhteen, tai se on edistynyt 90º: ta suhteessa siihen, kuten suositeltavaa. Joka tapauksessa taajuus on sama.

Kun x_C Se on erittäin suuri, virta on yleensä pieni ja tekee X: n äärettömän arvon_C, Lauhdutö käyttäytyy kuin avoin piiri ja virta on nolla.

[TOC]

Kuinka laskea kapasitiivinen reaktanssi

Katsotaanpa esimerkki kapasitiivisen reaktanssin laskemisesta: Oletetaan, että 6 μF -kondensaattori on kytketty vuorottelevaan tehon poistoaukkoon ja taajuuteen ja taajuuteen F 60 Hz.

Kapasitiivisen reaktanssin löytämiseksi käytetään alussa annettua määritelmää. Kulmataajuus ω annetaan:

Se voi palvella sinua: magneettinen induktio: kaavat, miten se lasketaan ja esimerkkejä

Ω = 2πf = 2π x 60 hz = 377 s^-1

Sitten tämä tulos korvataan määritelmässä:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohmi

Katsotaan nyt piirissä kiertävän virran amplitudi. Koska lähde tarjoaa amplitudijännitteen V_C = 40 V, käytämme kapasitiivisen reaktanssin, virran ja jännitteen välistä suhdetta maksimivirran tai virran amplitudin laskemiseksi:

Yllyttää_C = V_C / X_C = 40 V / 442.1 ohm = 0.09047 A = 90.5 m a.

Jos taajuudesta tulee erittäin suuri, kapasitiivinen reaktanssi tulee pieneksi, mutta jos taajuudesta tulee 0 ja meillä oli suoravirta, reaktanssi olisi yleensä ääretön.

Virran ja lauhduttimen jännite

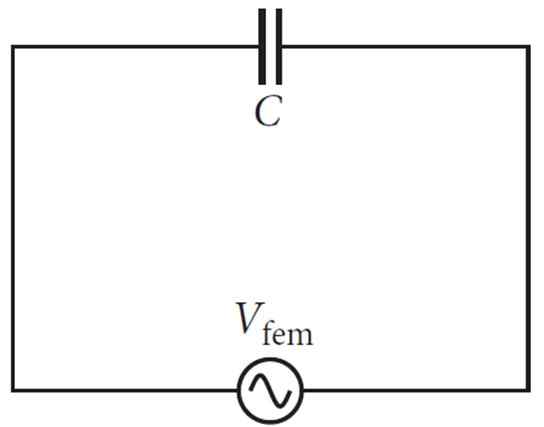
Kun lauhduttelija muodostaa yhteyden vuorottelevaan virran lähteeseen, kuten se värähtelee ja muuttaa sen napaisuutta, kondensaattori kokee kuormituksen ja purkautumisen vuorotellen.

Esimerkin kaltaisella taajuudella 60 Hz: n jännite on positiivinen 60 kertaa sekunnissa ja negatiivinen vielä 60 kertaa sekunnissa.

Kuva 2. Yksinkertainen lauhduttimen piiri ja vaihtovirtalähde. Lähde: f. Zapata.

Lisäämällä jännitettä, se ajaa virtaa yhteen suuntaan, mutta jos lauhdutin lataa, virta tapahtuu vastakkaiseen suuntaan, joka vastustaa ensimmäistä.

Kyllä v_C (t) = v_m Sen ωt, tietäen, että kapasiteetti on syy kuorman ja jännitteen välillä, meillä on kuorma:

C = q/v → q (t) = cv = cv_m Sent

Ja kun kuorma on ajasta riippuen, meillä on virta, joka on johdannainen:

Yllyttää_C(t) = CV_m Ω cos ωt

Mutta rinta ja kosini liittyvät: cos α = sin (α + π/2), siksi:

Yllyttää_C(t) = CV_m Ω Sen (ωt + π/2) = i_C Sen (ωt + π/2)

I: n kanssa_C = CV_C Ω

Kuten voidaan nähdä, virrasta on 90º etukäteen ja jännitteen suhteen, kuten alussa kommentoidaan.

Voi palvella sinua: Millikan -kokeilu: Menettely, selitys, merkitys

Tämän tyyppisten piirien kuvauksessa käsite Fasor, joka näyttää paljon vektorilta ja antaa mahdollisuuden edustaa monimutkaisessa tasossa minkä tahansa vuorottelevan määrän, kuten virta, jännite tai impedanssi.

Seuraava kuva osoittaa oikealla puolella kondensaattorin jännitteet ja virran fasorit, jotka muodostavat kulman 90º, mikä on viive näiden kahden välillä.

Vasemmalla puolella ovat vastaavat kaaviot, eri amplitudit, mutta sama taajuus. Ajan myötä virta etenee jännitteeseen ja kun tämä on maksimiarvo, virta on nolla ja kun jännite on nolla, virta on maksimi, mutta käänteisen napaisuuden kanssa.

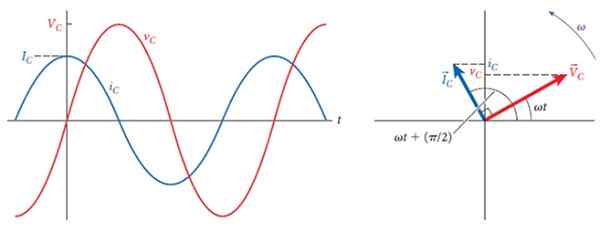Kuva 3. 90º viive virran ja jännitteen välillä kondensaattorin kautta. Lähde: Bauer, W.

Monimutkainen lauhduttimen impedanssi

Resistensseissä, kondensaattoreissa ja induktansseissa, reaktanssi on z -impedanssin kuvitteellinen osa, monimutkainen määrä, jolla vuorotellen virran piireissä on samanlainen kuin suoravirtavirran sähkövastuksen rooli.

Itse asiassa piirin impedanssi määritellään syyksi jännitteen ja virran välillä:

Z = v / i

Kondensaattorille tai kondensaattorille sen impedanssi antaa osamäärällä:

Z -z_C = v (t) / i (t) = v_C Sen ωt / i_C Sen (ωt + π/2)

Tapa ilmaista jännitettä ja virtaa fasoreina on osoittaa amplitudi ja vaihekulma (polaarinen muoto):

v (t) = v_C ∠ 0º

I (t) = i_C 90º

Siksi:

Z -z_C = V_C ∠ 0º / I_C ∠ 90º = (v_C / Yo_C) ∠ 0º -90º =

= V_C / CV_C Ω ∠ -90º = (1/ ωc) ∠ -90º =

Z -z_C = (- j) x_C

Toisin sanoen lauhduttimen impedanssi on sen kapasitiivinen reaktanssi kerrottuna kuvitteellisen yksikön negatiivilla.

Sarjan RC -piirin impedanssi

Vaihtovirtapiirin impedanssi, jolla on vastus, kondensaattorit ja induktorit voidaan myös edustaa binomiaalisesti:

Se voi palvella sinua: Termodynamiikan ensimmäinen laki: kaavat, yhtälöt, esimerkit

Z = r + jx

Tässä yhtälössä R edustaa vastusta, joka vastaa todellista osaa, j on kuvitteellinen yksikkö ja x on reaktanssi, joka voi olla kapasitiivinen tai induktiivinen tai molempien yhdistelmä, jos näitä elementtejä on läsnä samanaikaisesti piirissä.

Jos piiri sisältää vastus- ja sarjakondensaattorin, sen impedanssi on:

Z = z_{R -} + Z -z_C    

Kuten vastusjännitteessä ja virrassa ovat vaiheessa, resistiivinen impedanssi on yksinkertaisesti vastusarvo r.

Kapasitiivisen impedanssin tapauksessa olemme jo nähneet, että z_C = -Jx_C , Siksi RC -piirin impedanssi on:

Z = r - jx_C = R - J (1/ ωc)

Esimerkiksi alla esitetyssä piirissä, jonka lähde on muodoltaan:

100 V ⋅ SEN (120πt)

Tarkkailemalla, että ω = 120π, impedanssi on:

Z = 83.0 - J [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 J ohm.

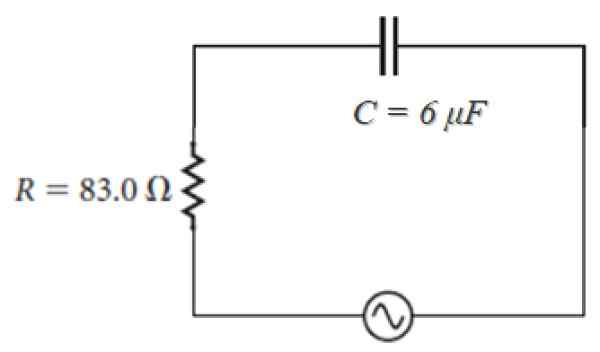Kuva 4. RC Circuit -sarja, jossa on vaihtovirtalähde. Lähde: f. Zapata.

Kapasitiiviset reaktanssisovellukset

PASA: n korkeat suodattimet, alhaiset suodattimet, siltapiirit kapasitanssien ja induktanssien ja jääkaappipiirien mittaamiseksi ovat pääpiirisovelluksia, jotka sisältävät kapasitiivisia reaktioita, yhdessä induktanssien ja sähkövastuksen kanssa.

Äänilaitteissa joissain kaiuttimissa on erillisiä tyyppejä BASSOKAIUTIN (suurempi) matalataajuuksille ja Tweetter tai pieni sarvi korkeille taajuuksille. Tällä tavoin äänen suorituskyky ja laatu paranee.

Niitä käytetään kondensaattoreita, jotka estävät matalien taajuuksien saapumista tweeteriin, kun taas induktori lisätään bassokaiuttimeen korkeataajuussignaalien välttämiseksi, koska induktanssilla on reaktanssi, joka on verrannollinen taajuuteen: x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x X_Lens = 2πfl.

Viitteet

1. Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. MC Graw Hill.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Nide 2. MC Graw Hill.
3. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 6. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
5. Serway, R., Jewett, J. 2008. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.