Mikä on lineaarinen nopeus? (Ratkaistujen harjoitusten kanssa)

Se Lineaarinen nopeus Se on määritelty sellaiseksi. Jos hiukkanen liikkuu aina suoraviivaisen radan aikana, ei ole mitään ongelmaa kuvitella, kuinka nopeusvektori seuraa tätä suoraa linjaa.

Yleensä liike tapahtuu kuitenkin käyrällä mielivaltaisesti. Jokainen käyrän osa voidaan mallintaa ikään kuin se olisi osa radioympyrää -lla, joka jokaisessa vaiheessa on tangentti polulle.

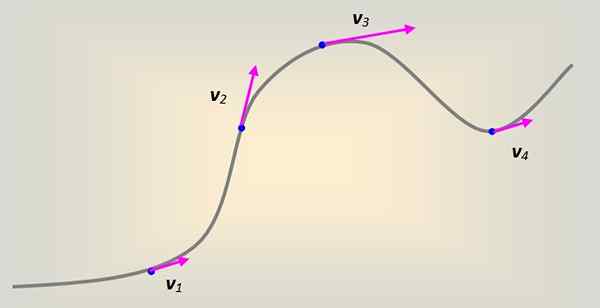
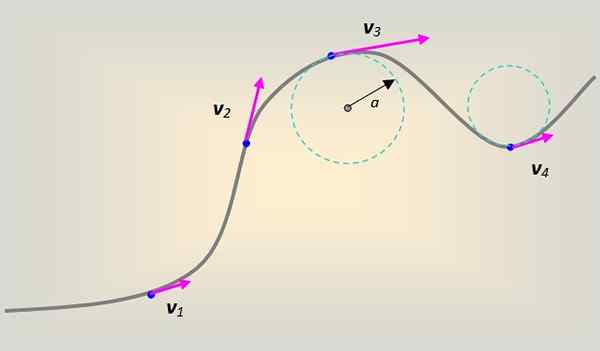Kuvio 1. Lineaarinen nopeus matkapuhelimella, joka kuvaa kaarevaa etenemissuuntausta. Lähde: Itse tehty.

Tässä tapauksessa lineaarinen nopeus liittyy tangentiaalisesti ja aina käyrälle jokaisessa pisteessä.

Matemaattisesti välitön lineaarinen nopeus on aseman johdannainen ajan suhteen. Olla r - hiukkasen sijaintivektori heti t, Sitten lineaarinen nopeus antaa lausekkeella:

v = r -'(T) = Dr - / DT

Tämä tarkoittaa, että lineaarinen nopeus tai tangentiaalinen nopeus, kuten sitä kutsutaan, ei ole muuta kuin aseman muutos ajan suhteen.

[TOC]

Lineaarinen nopeus pyöreässä liikkeessä

Kun liike on kehällä, voimme mennä hiukkasen viereen kussakin pisteessä ja nähdä, mitä tapahtuu kahdessa erityisessä suunnassa: yksi niistä on se, joka osoittaa aina keskustaan. Tämä on osoite säteilevä.

Toinen tärkeä suunta on se, joka tapahtuu kehällä, tämä on osoite tangentiaalinen Ja lineaarisella nopeudella on aina se.

Voi palvella sinua: Manometrinen paine: Selitys, kaavat, yhtälöt, esimerkit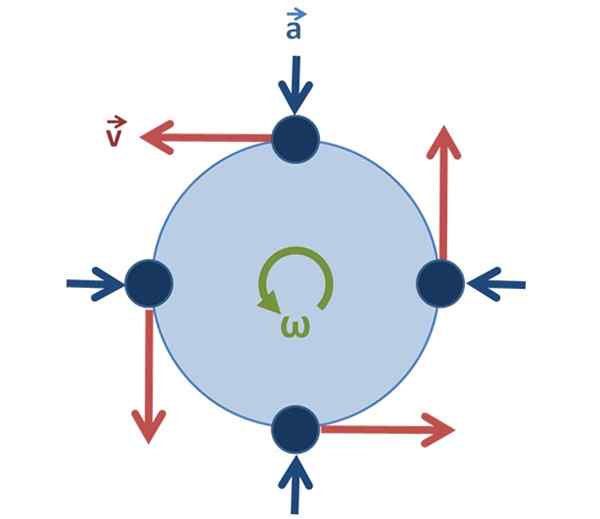Kuva 2. Tasainen pyöreä liike: nopeusvektori muuttaa suuntaa ja suuntaa hiukkasen pyöriessä, mutta sen suuruus on sama. Lähde: Alkuperäinen käyttäjä: Brews_ohare, käyttäjän svged: sjlegg [cc by-Sa 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Yhdenmukaisen pyöreän liikkeen tapauksessa on tärkeää kyllä, se pysyy muuttumattomana.

Tätä liikettä varten asento on ajan funktiona S (t), missä s onko hän Tourd -kaari ja t On aika. Tällöin ilmaisua koskeva nopeus antaa hetkellisen nopeuden V = ds/dt Ja se on vakio.

Jos myös nopeuden suuruus vaihtelee (tiedämme jo, että suunta aina tekee sen, muuten matkapuhelin ei pystynyt kääntymään), meillä on monipuolinen pyöreä liike, jonka aikana liikkuva pyörien lisäksi se voi pysäyttää tai kiihdyttää.

Lineaarinen nopeus, kulmanopeus ja keskikiristyskiihtyvyys

Hiukkasliike voidaan nähdä myös lakaisukulma, Sen sijaan, että se tekisi maalista. Tässä tapauksessa puhuu kulmanopeus. Radioympyrän liikkeelle R -, Kaaren (radiaaneissa) ja kulman välillä on suhde:

S = r θ

Johdetaan molemmin puolin:

ds/dt = r (dθ/dt)

Kutsu θ: n johdannainen suhteessa t kuten kulmanopeus Ja merkitsemällä sitä kreikkalaisella kirjaimella ω "omega", sinulla on tämä suhde:

v = ωR -

Centripetaalinen kiihtyvyys

Jokaisella pyöreällä liikkeellä on centripetaalinen kiihtyvyys, Se on aina suunnattu ympärysmiipan keskustaan. Hän huolehtii siitä, että nopeus muuttuu liikkumaan hiukkasen kanssa, kun se kääntyy.

Se voi palvella sinua: Kalibrointikäyrä: Mihin se on, miten se tehdään, esimerkkejä

Centripetaalinen kiihtyvyys -lla_c jompikumpi -lla_{R -} Se osoittaa aina keskustaan ​​(katso kuva 2) ja liittyy tällä tavalla lineaariseen nopeuteen:

-lla_c = v² /R

Ja kulmanopeudella seuraavasti:

-lla_c = (ΩR)² /R = ω²R -

Tasaiselle pyöreälle liikkeelle, sijainti S (t) Se on muodoltaan:

S (t) = SO+ VT

Lisäksi monipuolisella pyöreällä liikkeellä on oltava komponentti kiihtyvyydestä Tangentiaalinen kiihtyvyys -lla_T, joka käsittelee lineaarisen nopeuden suuruuden muuttamista. Joo -lla_T  se on vakio, Asema on:

S (t) = s_jompikumpi + v_jompikumpiT + ½ a_Tt²

Kanssa v_jompikumpi Kuten alkuperäinen nopeus.

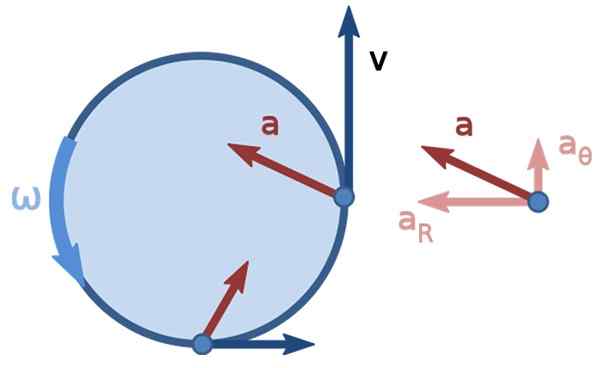Kuva 3. Epäyhtenäinen pyöreä liike. Lähde: epäyhtenäinen_circular_motion.PNG: panimot oharedorivatiiviset työt: Kooning Jons [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Ratkaistu lineaarinen nopeusharjoitukset

Ratkaisut harjoitukset auttavat selventämään annettujen käsitteiden ja yhtälöiden asianmukaista käyttöä.

-Liikunta ratkaistiin 1 

Hyönteinen liikkuu sädeellä puolipyöreällä r = 2 m, alkaen leposta pisteessä A lisäämällä sen lineaarista nopeutta, nopeudella p m/s². Löydä: a) Mihin aikaan se saavuttaa pisteen B, b) lineaarisen nopeuden vektori tuolloin, c) vektorikiihtyvyys tuolloin.

Kuva 4. Hyönteinen alkaa A: sta ja saavuttaa B: n puolipyöreällä radalla. Sillä on lineaarinen nopeus. Lähde: Itse tehty.

Ratkaisu

a) Lausunto osoittaa, että tangentiaalinen kiihtyvyys on vakio ja se on π m/s: n arvoinen², Silloin on kelvollista käyttää yhtälöä tasaisesti vaihtelevalle liikkeelle:

S (t) = s_jompikumpi + v_jompikumpiT + ½ a_T.t²

S: n kanssa_jompikumpi = 0 ja V_jompikumpi = 0:

S (t) = ½ a_T.t²

S = πR - (Puolet kehän pituudesta)

T = (2. πR - --lla_T-A ^½ S = (2π.2 /π-A^½S = 2 s

b) v (t) = v_jompikumpi + -lla_T. T = 2π neiti

Kun pisteessä B, lineaarinen nopeusvektori osoittaa pystysuunnassa alaspäin (-ja)

Voi palvella sinua: mikä on dielektrinen vakio?

v (t) = 2π neiti(-ja-A

c) Tangentiaalinen kiihtyvyys on jo ollut, centripetaalista kiihtyvyyttä puuttuu nopeusvektori -lla-

-lla_c = v² / R = (2π-A² / 2 m/ s² = 2π² neiti²

-lla = a_c (-x) + a_T (-ja) = 2π²(-x)+ π (-ja) neiti²

-Liikunta ratkaistiin 2

Hiukkas kääntyy radioympyrässä 2.90 m. Tietyllä hetkellä sen kiihtyvyyden arvo on 1.05 m/s² Sellaiseen suuntaan, joka muodostuu 32 sen liikesuunnasta. Löydä lineaarinen nopeus kohdasta: a) tällä hetkellä, b) 2 sekuntia myöhemmin, olettaen.

Ratkaisu

a) Liikkeenosasto on juuri tangentiaalinen osoite:

-lla_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; -lla_C = 1.05 m/s² . SEN 32º = 0.56 m/s²

Nopeus puhdistuu -lla_c = v² / R kuten:

v = (r.-lla_c-A^1/2  = 1.27 m/s

b) Yhtälö tasaisesti vaihtelevalle liikkeelle on pätevä seuraavasti: V = V_jompikumpi + -lla_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fyysinen sarja tiedettä ja tekniikkaa. Osa 3. Painos. Kinematiikka. 199-232.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th… Ed Prentice Hall. 62-64.
4. Suhteellinen liike. Toipunut: kurssit.Lumenarning.com
5. Wilson, J. 2011. Fysiikka 10. Pearson -koulutus. 166-168.