Mitkä ovat sisäiset vaihtoehtoiset kulmat? (Harjoituksilla)

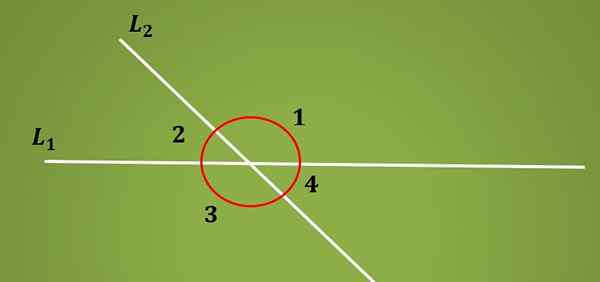
Se sisäiset vaihtoehtoiset kulmat Ne ovat ne kulmat, jotka muodostuvat kahden yhdensuuntaisen viivan leikkauskohdan ja poikittaisen viivan risteyksessä. Kun L1 -viiva leikataan poikittaisviivalla L2 4 -kulmasta muodostetaan.

Kaksi kulmaparia, jotka pysyvät samalla L1 -linjan puolella, kutsutaan lisäkulmiksi, koska sen summa on yhtä suuri kuin 180º. Alemmassa kuvassa kulmat 1 ja 2 ovat täydentäviä, samoin kuin kulmat 3 ja 4.

Jotta voidaan puhua sisäisistä vaihtoehtoisista kulmista, on välttämätöntä olla kaksi yhdensuuntaista viivaa ja poikittainen viiva; Kuten aiemmin nähdään, muodostuu kahdeksan kulmaa.

Kun poikittaisviivalla on kaksi yhdensuuntaista viivaa L1 ja L2, muodostuu kahdeksan kulmaa, kuten seuraavassa kuvassa on havainnollistettu.

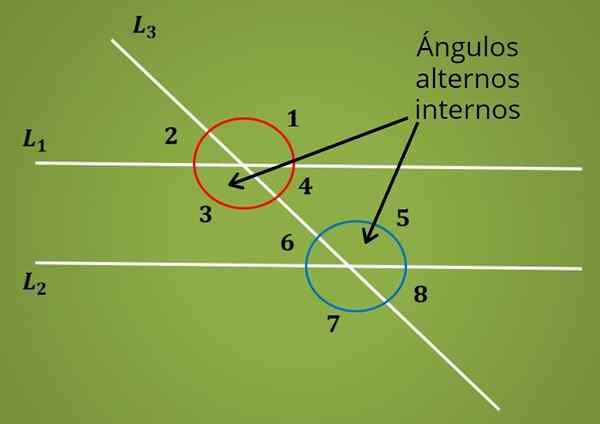
Ylemmässä kuvassa kulmien 1 ja 2, 3 ja 4, 5 ja 6, 7 ja 8 parit ovat lisäkulmia. 

Nyt sisäiset vaihtoehtoiset kulmat ovat kahden yhdensuuntaisen viivan L1 ja L2 välissä, mutta ne sijaitsevat poikittaisen viivan L2 vastakkaisilla puolilla. Tuo on Kulmat 3 ja 5 ovat sisäisiä vaihtoehtoisia. Samoin kulmat 4 ja 6 ovat sisäisiä vaihtoehtoisia kulmia.

Vastakkaiset kulmat kärjessä

Sisäisten vaihtoehtoisten kulmien hyödyllisyyden tuntemiseksi on ensin tarpeen tietää, että jos kärkipiste vastustaa kahta kulmaa, nämä kaksi kulmaa mittaavat samat.

Esimerkiksi kulmat 1 ja 3 mittaavat samat kuin kärkivalta vastustaa niitä. Saman päättelyn mukaan voidaan päätellä, että kulmat 2 ja 4, 5 ja 7, 6 ja 8 mittaavat saman.

Kulmat muodostuvat sekaanilaisten ja kahden rinnakkaisten väliin

Kun on kaksi rinnakkaista viivaa, jotka on leikattu kuivalla tai poikittaisella viivalla, kuten edellisessä kuvassa, on totta, että kulmat 1 ja 5, 2 ja 6, 3 ja 7, 4 ja 8 mittaavat samat.

Voi palvella sinua: Euler -numero tai numero E: Kuinka paljon OK, ominaisuudet, sovellukset

Sisäiset vaihtoehtoiset kulmat

Käyttämällä kärkipisteen asettamia kulmia ja secant- ja kahden yhdensuuntaisten viivojen välillä muodostuneiden kulmien ominaisuuksia, voidaan päätellä, että sisäisillä vaihtoehtoisilla kulmilla on sama mitta.

Ratkaisut

- Ensimmäinen harjoitus

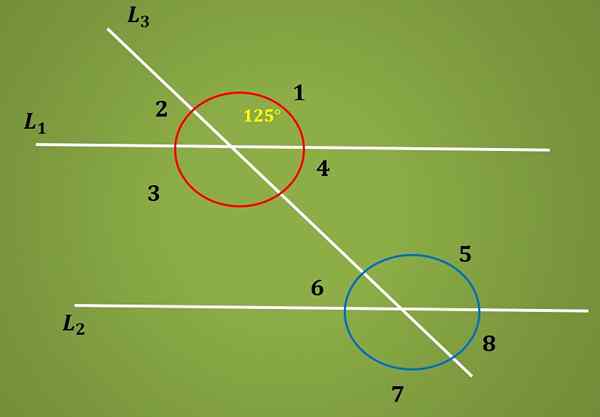
Laske seuraavan kuvan kulman 6 mitta, tietäen, että kulma 1 mittaa 125º.

Ratkaisu

Koska kärkipiste on vastapäätä kulmia 1 ja 5, sinulla on kulma 3 mittaa 125º. Nyt, koska kulmat 3 ja 5 ovat sisäisiä vaihtoehtoisia, sinulla on myös kulma 5 mittaa 125º.

Lopuksi, koska kulmat 5 ja 6 ovat lisäyksiä, kulman 6 mitta on yhtä suuri kuin 180º - 125º = 55º.

- Toinen harjoitus

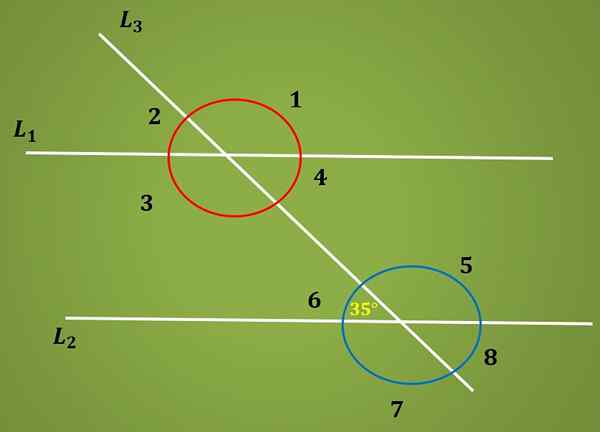
Laske kulma 3 tietäen, että kulma 6 mittaa 35º.

Ratkaisu

On tiedossa, että kulma 6 mittaa 35º, ja tiedetään myös, että kulmat 6 ja 4 ovat sisäisiä vaihtoehtoisia, siksi ne mittaavat saman. Toisin sanoen kulma 4 mittaa 35º.

Toisaalta käyttämällä sitä tosiasiaa, että kulmat 4 ja 3 ovat täydentäviä, kulman 3 mitta on yhtä suuri kuin 180º - 35º = 145º.

Havainto

On välttämätöntä, että viivat ovat yhdensuuntaisia, jotta ne voivat täyttää vastaavat ominaisuudet.

Harjoitukset voidaan ratkaista nopeammin, mutta tämä artikkeli halusi käyttää sisäisten vaihtoehtoisten kulmien omaisuutta.

Viitteet

1. Bourke. (2007). Kulma geometrian matematiikan työkirja. NewPath Learning.
2. Clemens, S. R -., O'Dafer, P. G., & Cooney, T. J -. (1998). Geometria. Pearson -koulutus.
3. Lang, s., & Murrow, G. (1988). Geometria: Lukiokurssi. Springer Science & Business Media.
4. Lira, a., Jaime, P., Chavez, m., Gallegos, m., & Rodríguez, c. (2006). Geometria ja trigonometria. Umbral Editions.
5. Moyano, a. R -., Saro, a. R -., & Ruiz, R. M. (2007). Algebra ja neliöinen geometria. Netbiblo.
6. Sullivan, M. (1997). Trigonometria ja analyyttinen geometria. Pearson -koulutus.
7. Wingard-Enelson, R. (2012). Geometria. ENLLOW Publishers, Inc.

Voi palvella sinua: implisiittiset johdannaiset: miten ne on ratkaistu ja ratkaistuihin harjoituksiin