Konvergenssiradion määritelmä, esimerkit ja harjoitukset ratkaistu

Hän Konvergenssisäde Sarja voimia on lähentymisympyrän säde, johon sarja lähenee. Tämä ympyrä ulottuu arvosta, joka peruuttaa voiman pohjan sarjaan liittyvän funktion lähimpään singulaarisuuteen.

Kaikki analyyttiset toiminnot f (z) Se on yhdistänyt sarjan voimia ei -singular -pisteen ympärille, nimeltään Taylor -sarja:

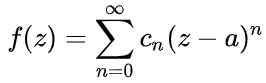
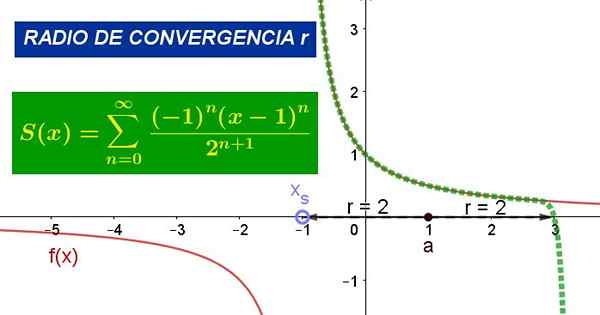
Kuvio 1. Kaavio näyttää virtalähteen arvon A = 1 funktion f (x). Sen lähentymissäde on r = 2. Lähde: Fanny Zapata.

Missä -lla Se on lähentymisympyrän keskipiste, z -z funktion riippumaton muuttuja ja c_n Ne ovat kertoimia, jotka liittyvät toiminnasta johdettuihin F asiaan z = a.

Konvergenssisäde r - Se on positiivinen reaaliluku, joka määrittelee alueen:

| Z - A | < r

Missä sarja lähentyy. Tältä alueelta Diverge -sarja, toisin sanoen se vie äärettömät arvot. Kun lähentymissäde on ääretön, sarja lähentyy koko kompleksissa.

[TOC]

Kuinka lähentymissäde määritetään?

Jotta sarja olisi lähentynyt, on välttämätöntä, että peräkkäisten termien absoluuttinen arvo vähenee, kun termien lukumäärä on erittäin suuri. Matemaattisella tavalla se ilmaistaan ​​seuraavasti:

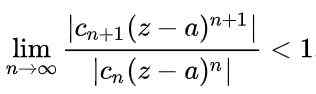
Käyttämällä edellisen lausekkeen rajojen ominaisuuksia, se saadaan:

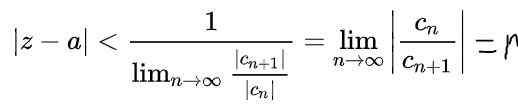
Tässä r - Se on lähentymisen säde ja | Z - A | < r Se on avoin reunapiiri monimutkaisessa tasossa, jossa sarja lähentyy. Jos arvo -lla Ja muuttuja Z ovat reaalilukuja, sitten oikean akselin avoin lähentymisväli on: (A - R, A+R).

Taylor -sarja

Funktion Taylor -sarja f (x) Noin arvo -lla Jossa funktiossa on äärettömiä johdannaisia, se on valtuuksien sarja, joka on määritelty:

Se voi palvella sinua: todennäköisyyden aksioomit: tyypit, selitys, esimerkit, harjoitukset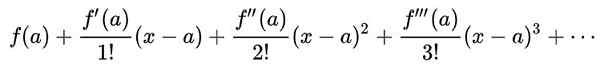

Ympäristössä Ja X - A | < r, kanssa r - kutenSarjan, Taylor -sarjan ja funktion on oltava f (x) Ne osuvat samaan aikaan.

Toisaalta lähentymissäde r - Se on pisteen etäisyys -lla ja singulaarisuus x_s lähempänä asiaa -lla, ovat yksittäiset pisteet arvot, joissa funktion rajalla on taipumus äärettömyyteen.

Eli milloin x → x_s niin F → ± ∞.

Esimerkit

Esimerkki 1

Olla S (x) Seuraavan lausekkeen antamat voimat:

S (x) = 1 - x + x²- x³+ x⁴-.. .+(-1)ⁿ ⋅ xⁿ +.. .

Alueen määrittämiseksi, jolla sarja lähentyy, laskemme käsitteen (n-beeimo + 1) ja termin (N-ENE) välillä:

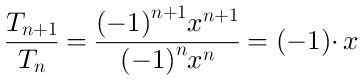
Etuosan absoluuttinen arvo on | x | ja sen raja milloin N → ∞ se on myös  | x |.

Jotta sarja olisi lähentävä, on välttämätöntä, että:

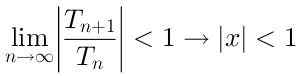
Joten tämän sarjan lähentymissäde on R = 1, Koska se lähenee X: n arvoja, jotka ovat etäisyydellä alle 1 suhteessa keskustaan x = 0.

Esimerkki 2

Haluat löytää taylor -sarjan funktion f (x) = 1 / (1 + x) ympärillä x = 0 ja määritä sen lähentymissäde.

Sarjan löytämiseksi otamme funktion f (x) peräkkäiset johdannaiset, joista näytämme kolme ensimmäistä:

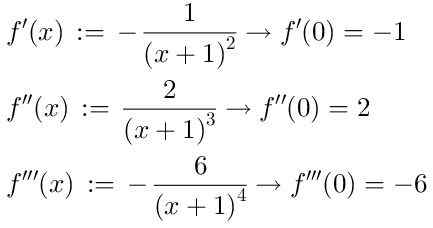
Kun otetaan huomioon, että Taylor -sarjan nollajärjestys on:

 f (0) = 1,

Ensimmäinen tilaus: F '(0)/1!

Toinen tilaus:

 F "(0)/2!

Kolmas järjestys:

 f "(0)/3!

Ja niin edelleen, annetun funktion Taylor -sarja on:

f (x) = 1 - x + x² - x³ + x⁴ -.. .+(-1)ⁿ ⋅ xⁿ +.. .

Voi palvella sinua: Tasasivuinen kolmio: Ominaisuudet, ominaisuudet, kaavat, alue

Joka on samaan aikaan esimerkissä 1 tutkittujen voimarjojen kanssa.

Olemme jo sanoneet, että Taylor -sarjan lähentymissäde on etäisyys sarjan laajennuksen keskustasta, mikä meidän tapauksessamme on arvo x = 0 funktion ensimmäiseen singulaarisuuteen asti f (x). 

Koska toiminnassamme on yksinäisyys (ts. Äärettömyys) x = -1, Arvon välinen etäisyys -1 ja laajennuskeskus 0 - On | -1 - 0 | = 1, Johtopäätöksenä on, että Taylor -sarjan lähentymissäde on 1.

Tämä tulos osuu täysin esimerkissä 1 saatuun toisella menetelmällä.

Se tosiasia, että Taylor-sarjan lähentymisvyöhyke on avoin aikaväli (-1, 1), viittaa siihen, että funktio ja sarja ovat samat tällä aikavälillä, mutta eivät saman ulkopuolella.

Se on esitetty kuvassa 2, jossa on otettu 41 Taylor -sarjan termejä, jotka on piirretty jatkuva sininen viiva, kun taas alkuperäinen funktio on esitetty segmenttien punaisella viivalla.

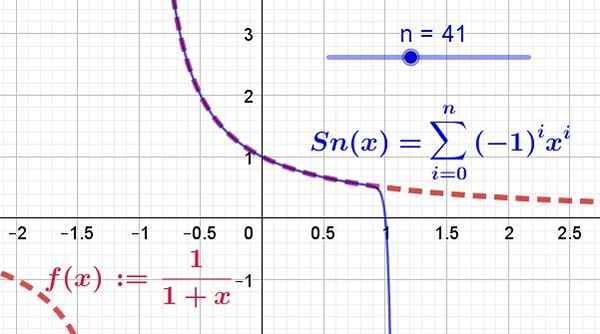Kuva 2. Funktio F (x) (punaisella) ja sen voimarisarja (tai Taylor -sarja sinisellä) on esitetty. Sitä voidaan pitää sarjan ensimmäisinä 41 -termina, jotka ovat välillä -1 ja 1. Lisäksi funktio ja sen sarja ovat samat vain lähentymisalueella. (Lähde: Fanny Zapata)

Ratkaisut

- Harjoitus 1

Harkitse samaa toimintoa f (x) = 1 / (1 + x) esimerkiksi 2, mutta tällä kertaa pyydetään löytämään Taylor -sarjan mainitun toiminnon sarja pisteen A = 1 ympärille.

Ratkaisu

Löydämme sarjan peräkkäiset ehdot, alkaen riippumattomasta termistä, joka on F (1) = ½.

Seuraava ensimmäisen tilauksen termiä vastaava kertoimet on:

F '(1)/1! = -¼

Toinen järjestys on:

f "(1)/2! = 2/(2³ 2!-A

Noudata kolmannen tilauskerrointa:

Se voi palvella sinua: tetradecágon

f "(1)/3! = -6 / (2⁴ 3!-A

Ja niin edelleen. Taylor -sarja on:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Harjoitus 2

Etsi edellisen sarjan lähentymissäde

Ratkaisu

Kirjoitamme termin N-ENE ja termi n-alkaus enemmän:

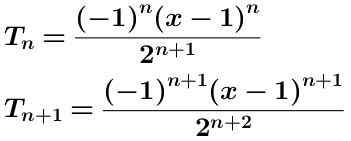Laskemme näiden kahden termin osamäärän, joka on esitetty alla yksinkertaistettu:

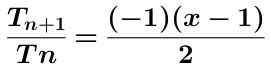
Edellisen lausekkeen absoluuttinen arvo otetaan hankkimalla:

Ja X - 1 | / 2

Jotta sarja olisi lähentynyt, on kuitenkin välttämätöntä, että edellinen määrä on tiukasti alhaisempi kuin yksikkö, ts

Ja X - 1 | < 2

Mikä osoittaa, että arvon x = 1 ympärillä oleva lähentymissäde on:

R = 1

Toisaalta edellinen lauseke vastaa kaksinkertaista eriarvoisuutta:

-2 < x - 1 < +2

Jos lisäämme +1 edellisen lausekkeen kolmeen jäseneen, se saadaan:

-1 < x < 3

Joka on sarjan lähentymisväli.

Kuvio 1 esittää alkuperäisen funktion ja taylor -sarjan mainitun funktion ympärillä x = 1. Kuvassa voidaan varmistaa, että sarja on samanaikainen pisteen X = 1 ympäristössä, mutta lähentymissädeellä.

Viitteet

1. CK-12-säätiö. Power -sarja: toimintojen ja toimintojen esitys. Toipunut: CK12.org.
2. Engler, a. 2019. Kiinteä laskenta. Rannikon kansallinen yliopisto.
3. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
4. Ilmaiset matematiikan tekstit. Power -sarja. Toipunut: matematiikka.Libretext.org.
5. Wikipedia. Power -sarja. Palautettu: on.Wikipedia.org.
6. Wikipedia. Lähentymissäde. Haettu: vuonna.Wikipedia.org