3 n neliöjuuri (helppo ratkaisu ja selitys)

3: n neliöjuuri on 1,73205080756877.

Se voidaan ilmaista:

√3 = 1,73205080756887

Tietää mikä on 3 neliöjuuri, On tärkeää tietää numeron neliöjuuren määritelmä. Annetaan positiivinen luku "a", "a" -numero, jonka merkitään √a, on positiivinen luku "B" siten, että kun "B" kerrotaan sillä, tulos on "A".

Matemaattinen määritelmä sanoo: √a = b kyllä, ja vain jos, b² = b*b = a. Siksi tietää, mikä on 3: n neliöjuuri, ts. √3: n arvo, on löydettävä b -numero, että b² = b*b = √3.

Lisäksi √3 on irrationaalinen luku, joka koostuu äärettömästä ei -jaksollisesta määrästä desimaaleja. Tästä syystä on vaikea laskea 3: n neliöjuuri manuaalisesti.

3 neliöjuuri

Jos käytetään laskinta, voidaan nähdä, että 3: n neliöjuuri on 1,73205080756887…

Nyt voit yrittää manuaalisesti arvioida tämän numeron seuraavasti:

-1*1 = 1 ja 2*2 = 4, tämä sanoo, että 3: n neliöjuuri on luku välillä 1 - 2.

-1,7*1,7 = 2,89 ja 1,8*1,8 = 3,24, siksi ensimmäinen desimaalikuva on 7.

-1,73*1,73 = 2,99 ja 1,74*1,74 = 3,02, joten toinen desimaalin tarkkuudella on 3.

-1,732*1,732 = 2,99 ja 1,733*1,733 = 3,003, siis kolmas desimaalia on 2.

Ja niin edelleen voit jatkaa. Tämä on manuaalinen tapa laskea 3: n neliöjuuri.

On myös muita paljon edistyneempiä tekniikoita, kuten Newton-Raphson-menetelmä, joka on numeerinen menetelmä likiarvojen laskemiseksi.

Mistä löydämme numeron √3?

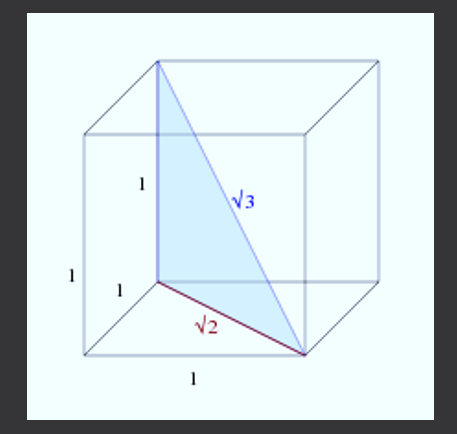
Monimutkaisen numeron vuoksi voidaan ajatella, että se ei näy jokapäiväisissä esineissä, mutta tämä on väärä. Jos sinulla on kuutio (neliölaatikko), niin että sen sivujen pituus on 1, kuution diagonaalien mitta on √3.

Tämän varmistamiseksi käytetään Pythagoras -lausetta, joka sanoo: Anna.

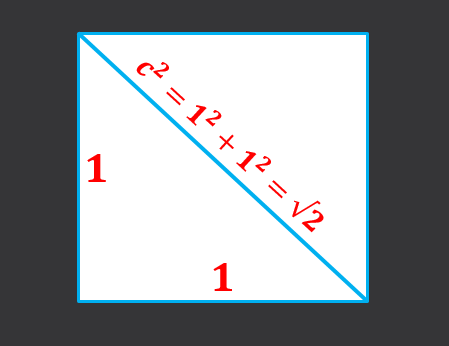
Side 1: n sivulla on, että sen pohjan neliön diagonaali on yhtä suuri kuin luokkien neliöiden summa, ts. C² = 1²+1² = 2, siksi perusmittauksen diagonaali √2.

Nyt kuution diagonaalin laskemiseksi näet seuraavan kuvan.

Uudessa suorakulmiokolmiossa on pituudet 1 ja √2, siksi käytettäessä Pythagoras -lausetta laskemaan sen diagonaalin pituus: c² = 1²+(√2) ² = 1+2 = 3, sanotaan, että sanotaan , C = √3.

Siten sivukauhan 1 diagonaalin pituus on yhtä suuri kuin √3.

√3 Irrationaalinen numero

Alussa sanottiin, että √3 on irrationaalinen luku. Tämän varmistamiseksi oletetaan absurdi, joka on rationaalinen luku, jonka on olemassa kaksi numeroa "A" ja "B", suhteelliset serkut, kuten a/b = √3.

Kun viimeinen tasa -arvo ja selkeä “a²”, saadaan seuraava yhtälö: a² = 3*b². Tämä sanoo, että "a²" on kolmen monikerros, joka päättelee, että "A" on kolmen moninkertainen.

Koska "3 -osa on 3, on kokonaisluku" k ", että a = 3*k. Siksi korvaamalla toisessa yhtälössä se saadaan: (3*k) ² = 9*k² = 3*b², mikä on sama kuin b² = 3*k².

Kuten aikaisemmin, tämä viimeinen tasa -arvo johtaa siihen johtopäätökseen, että "B" on kolmen moninkertainen.

Yhteenvetona voidaan todeta, että "A" ja "B" ovat molemmat kolmen kerrannaisia, mikä on ristiriita, koska aluksi oletetaan, että ne olivat suhteellisia serkkuja.

Siksi √3 on irrationaalinen luku.