Toiset rivit

Tämän puutarhan oven puu on halukas siten, että ne määrittävät kuivat linjat. Lähde: f. Zapata. Pxhere.com

Mitkä ovat kuivat linjat?

Koneessa, Toiset rivit Ne ovat niitä, jotka leikkaavat muut viivat ja käyrät. Kahden viivan tapauksessa sen leikkaus on kohta, kun taas käyrän sekoitusviiva leikkaa tämän kahdessa tai useammassa pisteessä.

Tarkkaile ylemmän kuvan aita huolellisesti. Siinä on piirretty useita suoria suoria värejä, jotka on merkitty nimellä L₁, Lens₂ ja minä₃. Molemmin puolin nuolet tarkoittavat, että linjat ovat pitkittyneitä määräämättömäksi.

No, linjat l₁, Lens₂ ja minä₃ Ne kuivaavat toisiaan, koska jokainen pari on leikattu violettipisteissä.

Lisäksi linjat l₁ ja minä₂, Kuten L₁ ja minä₃, Ne määrittävät 4 kulmaa toistensa kanssa, kaksi heistä akuutti ja toinen sotku, kun taas linjat L₂ ja minä₃ Ne ovat kohtisuorassa, mikä tarkoittaa, että niiden määrittämät 4 kulmaa ovat suorat.

Kaksi rinnakkaista viivaa ei voi koskaan olla kuivia, koska heidän tilansa vuoksi niillä ei ole sattumaa koskevia pisteitä. Samanaikaiset linjat eivät ole kuivia, koska niillä on enemmän kuin yksi yhteinen kohta.

Kuivauslinjojen ominaisuudet

• Kahdella sekanttiviivalla on ainutlaatuinen kohta risteyksessä.
• Kahden kuivauslinjan rinteiden on oltava erilaisia. Kyllä m₁ Se on linjan l kaltevuus₁, ja m₂ Se on linjan l kaltevuus₂, Sitten on täyttynyt, että m₁ ≠ m₂.
• Kahden kuivausviivan rinteet kohtisuorassa toisiinsa nähden, joiden vastaavat rinteet ovat m₁ ja m₂, He täyttävät suhteen m₁ = -1/ m₂. Lisäksi skalaarituote kahden vektorin välillä v ja tai Näihin linjoihin sisältyy nolla, koska skalaarituotteen määritelmä on v tai = v ∙ u ∙ cos θ, koska vektorien välinen kulma on.
• Linja voi olla käyrä tai muu geometrinen hahmo.
• Risteyttäessä kaksi kuivausviivaa tuottaa 4 kulmaa, identtiset kaksi kahteen tai identtisen kanssa toistensa kanssa.

Voi palvella sinua: Fraktioyhtälöt

Kuinka tietää, ovatko kaksi viivaa kuiva

Edellä kuvattujen kuivauslinjojen ominaisuuksista on mahdollista vahvistaa kolme kriteeriä tietää, ovatko kaksi linjaa kuivia:

-Rinteiden vertailu. Jos nämä ovat erilaisia, linjat ovat kuivia.

-Skalaarituotteen suorittaminen kahden näihin linjoihin sisältyvän vektorin välillä, nimeltään Johtajat. Jos skalaarituote on tyhjä, viivat ovat kuivia ja kohtisuorassa, ja jos se ei ole nolla, on mahdollista tietää niiden välillä, mikä on akuutti kulma, joka on olemassa viivojen välillä.

Edellyttäen, että tämä kulma on erilainen kuin 0º, viivat ovat kuivat ja jos se on yhtä suuri kuin 0º, niin se on yhdensuuntainen viivat.

-Laskemalla linjojen keskuudessa esiintyvä akuutti kulma, joka tunnetaan heidän rinteensä. Tämä voidaan tehdä kaavan kautta, joka liittyy mainitun kulman tangenttiin rinteillä.

Antaa m₁ ja m₂ rinteet ja θ niiden välinen akuutti kulma. Θ: n tangentti antaa:

Kuivauslinjojen tyypit

Kun kaksi riviä kuivuvat toisiaan, ne voivat olla seuraavat tyypit:

• Vino, Jos ne leikataan. Nämä kulmat ovat täydentäviä, toisin sanoen kulman mittasumma plus yksi täpärikulmasta on yhtä suuri kuin 180º. Kaikkiaan 4 kulman summa on yhtä suuri kuin 360º.
• Kohtisuorassa, Ne, jotka leikkaavat 4 kulmaa, jotka ovat yhtä suuret kuin 90º.

Kuinka löytää risteys kahden rivin välillä

Jos kaksi riviä kuivuvat, niillä on vain yksi leikkauspiste, joka ratkaisee kahden lineaarisen yhtälön järjestelmän kahdella tuntemattomalla. Jos viivat annetaan yleensä: ax + by = c, mainittu yhtälöjärjestelmä on:

Voi palvella sinua: ääretön sarja: Ominaisuudet, esimerkit

-lla₁x + b₁ y = c₁

-lla₂x + b₂ y = c₂

Kuinka löytää risteys linjan ja käyrän välillä

Tietäen sekä viivan että käyrän yhtälöt yhtälöjärjestelmää ehdotetaan ja joiden ratkaisut vastaavat risteyspisteitä. Jos järjestelmästä puuttuu ratkaisu, viiva ei ole käyrän kohdalla, eikä se ole, jos siellä on yksi leikkauspiste, koska siinä tapauksessa linja on tangentti käyrälle.

Jotta linja kuivuu, kuten alussa todettiin, yhtälöjärjestelmässä on oltava kaksi tai useampia ratkaisuja.

Esimerkkejä kuivauslinjoista

Cartesian lentokone

Cartesian taso määritetään kahdella viivalla, nimeltään X -akseli ja Akseli y, Vaaka- ja pystysuora, vastaavasti. Nämä viivat ovat kohtisuorassa ja niiden risteyspistettä kutsutaan Koordinaattijärjestelmän alkuperä, tai yksinkertaisesti alkuperä.

Monikulmion diagonaali

Polygon on tasainen kolmen tai useamman sivun kuva, joka liittyy pisteisiin, joita kutsutaan kärkipisteiksi. Segmentti, joka liittyy kahteen ei -säilytystilaan, on monikulmion diagonaali, ja mainittu segmentti sisältää linjan kyseiselle monikulmiolle.

Kehäköysi

Ympyrän köysi on segmentti, joka liittyy kahteen pisteeseen. Pääköys on halkaisija, joka välttämättä kulkee kehän keskustan läpi. No, linja, joka sisältää mitä tahansa köyttä, mukaan lukien halkaisija, on kuivausviiva kehään.

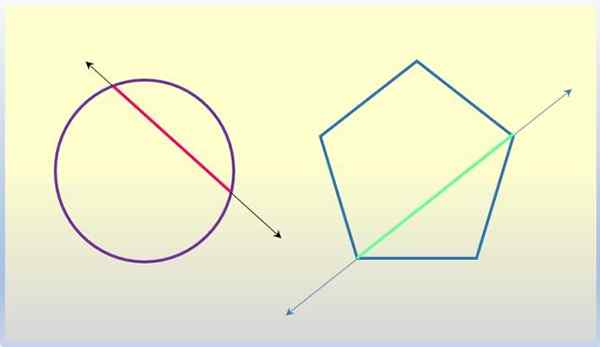Toiset viivat geometrisiin lukuihin. Lähde: f. Zapata.

Ristikkäin

Tällä työkalulla mutterit, jotka pitävät renkaat ajoneuvojen pyörille. Aseet muodostavat kuivia ja samanaikaisesti kohtisuorassa.

Voi palvella sinua: suhteellinen variaatio

Aakkoset Lyrics

Jotkut aakkoset kirjaimet koostuvat suorista iskuista, jotka määrittävät Secant. Esimerkiksi kirje X koostuu kahdesta iskuista, jotka on leikattu yhteen pisteeseen ja kirjain T koostuu kahdesta kohtisuorasta viivasta.

Ratkaisut

Harjoitus 1

Määritä, onko annettu viivat:

Lens₁ : y = 5x - 3

Lens₂ : y = -2x+1

Ratkaisu

Muodossa y = mx + b annetun viivan kaltevuus on M: n arvo, ts. X. Koska m₁ = 5 ja m₂ = -2, jotka ovat erilaisia, päätellään, että viivat ovat kuivat.

Harjoitus 2

Mikä on akuutti kulma harjoituksen 1 linjojen välillä?

Ratkaisu

M -arvot korvataan suoraan₁ = 5 ja m₂ = -2 edellisissä osissa annetussa kaavassa:

Siksi linjojen välinen kulma on θ = arctg 0.777… = 37.9º.

Harjoitus 3

Mikä on aiempien harjoitusten linjojen risteys?

Ratkaisu

Yhtälöjärjestelmää ehdotetaan seuraavasti:

Jonka ratkaisu on: x = 4/7; y = -1/7 (voidaan ratkaista millä tahansa yhtälöjärjestelmän resoluutiomenetelmillä tai laskimella).

Siksi viivojen leikkauspiste on: P (4/7; -1/7).

Viitteet

1. Analyyttinen geometria.Tiedot. Toiset rivit. Toipunut: geometriaanalitics.Tiedot.
2. Larson, r. 2006. Laskenta analyyttisellä geometrialla. Kahdeksas. Painos. McGraw Hill.
3. Linjat, jotka ylittävät. Toipunut: Teacheraltuna.com.
4. Requena, b. Toiset rivit. Toipunut: UniversOformulat.com.
5. Villena, m. Analyyttinen geometria R3: ssa. Haettu osoitteesta: dspace.Espoli.Edu.EY.