Vivusääntö

Mikä on vivusääntö?

Se vivusääntö Se on matemaattinen menettely, jonka avulla voidaan laskea fraktioiden, prosenttien tai määrien fraktioiden, prosenttimäärien tai määrien binaarisessa järjestelmässä. Se ei ole vain matemaattinen, vaan myös melko graafinen ja vakuuttava, se on erittäin hyödyllinen fysikaalis -kemiallisissa ja tekniikan laskelmissa.

Tämä sääntö koskee binaaristen järjestelmien vaihekaavioita riippumatta itse järjestelmän tyypistä. Toisin sanoen vaiheet voivat olla kiinteitä, kuten seosten kanssa; tai nestemäistä ja kaasumaista, kuten näemme nestemäisissä höyryn tasapainossa olevissa järjestelmissä.

Vivun fyysistä ja matemaattista periaatetta käytetään myös kemiallisiin tarkoituksiin ja materiaalien fysiikkaan. Lähde: Jimbowley, CC BY-SA 3.0, Wikimedia Commons

Vivusääntöä voidaan soveltaa suoraan ottaen huomioon abskissan akselin graafiset arvot, joissa maailmanlaajuiset fraktiot tai prosentuaaliset osuudet ovat yleensä nesteiden tapauksessa; tai tulenkestävä metallien tapauksessa heidän seoksissaan.

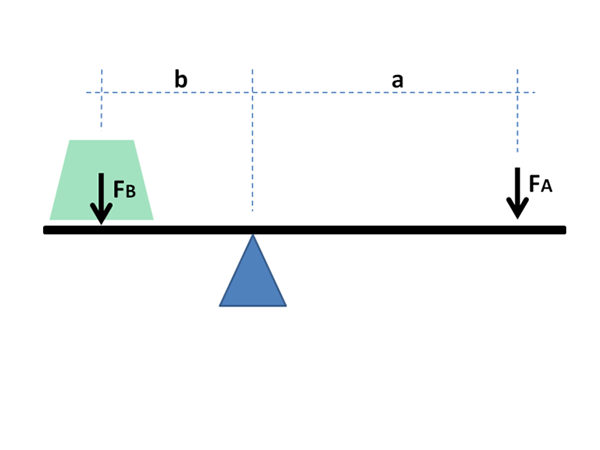
Kuten jäljempänä nähdään, sen nimi johtuu siitä valtavasta samankaltaisuudesta, joka sillä on matemaattisilla lausekkeilla, jotka osoittavat tasapainon kahden keinuvan päähän sijaitsevan massan välillä Fulcron kanssa.

Vipuvarsien on tasapainotettava kuormien massojen tasapainottamiseksi; Vaihekaavioiden, faasien fraktioiden ja moolien tapauksessa materiaalitasapainossa.

Selitys

Graafiset näkökohdat

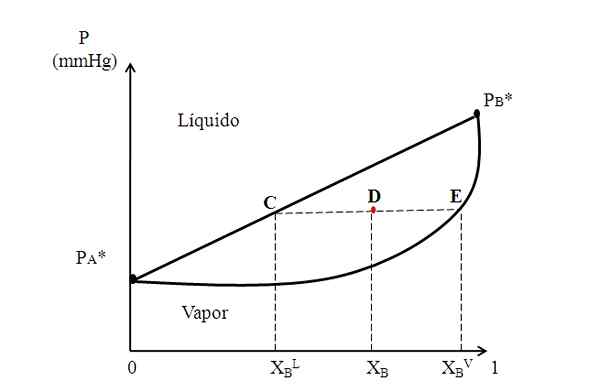Hypoteettinen binaarikaavio, jossa sitova viiva näyttää nesteen ja höyryfaasien koostumukset. Lähde: Gabriel Bolívar.

Yllä olevan kaavion keskellä meillä on alue, jolla nestemäinen ja höyryä ovat samanaikaisesti; Eli nestemäisen höyryn tasapainon alue. Tämän alueen yläpuolella A: n ja B: n seos on nestemäinen, ja sen alla on sooda alempien paineiden takia.

Harkitse nyt sekoitusta X -koostumuksella_{B -} ja jonka paine asettaa sen kohtaan D. Piirrämme pisteestä D vaakasuoran viivan, joka koskettaa viivaa ja käyrää sivuilla, lähtökohdat C ja E, vastaavasti. Tämä linja, joka kommunikoi pisteitä C, D ja E, C-D-E, tunnetaan nimellä Unionin linja ja projisoimalla sitä kohti akselia ja sen on annettava meille järjestelmän paine.

Se voi palvella sinua: Veden emäksisyys: Mikä on, päättäväisyys ja merkitys

Sitten näistä kohdista piirrämme muita viivoja kohtisuorassa sitoutumisviivaan, jotka pelaavat X -akselia. Kun piste E lepää höyrykäyrässä, silloin meillä on B: n molaarinen fraktio höyryvaiheessa (x_{B -}^V-A. Samoin kohta C, nesteen suorassa viivalla, antaa meille nestefaasissa olevan B: n molaarisen fraktion (x x_{B -}^Lens-A.

Vivusääntö perustuu tarkasti sitoutumislinjaan ja x: n välisiin etäisyyksiin_{B -}^Lens, X_{B -} ja x_{B -}^V.

Matemaattinen vähennys

B: n globaali molaarinen osuus on yhtä suuri kuin:

X_{B -} = n_{B -} / (n^Lens + n^V-A

Missä n_{B -} Ne ovat B: n kokonaismooleja sekä neste- että höyryfaasissa, ja n^Lens ja n^V ovat näiden vaiheiden vastaavat moolit. Puhdistus n_{B -} meillä tulee olemaan:

n_{B -} = X_{B -}n^Lens + X_{B -}n^V (1)

Toisaalta, n_{B -} Se on myös yhtä suuri kuin:

n_{B -} = n_{B -}^Lens + n_{B -}^V

= X_{B -}^Lensn^Lens + X_{B -}^Vn^V  (2)

Nyt yhtälöiden (1) ja (2) tasaaminen antaa meille:

X_{B -}n^Lens + X_{B -}n^V = X_{B -}^Lensn^Lens + X_{B -}^Vn^V

Ja järjestää uudelleen:

n^Lens(X_{B -} - X_{B -}^Lens) = n^V(X_{B -}^V - X_{B -}) (3)

n^Lens(C-d) = n^V(OF)

Nämä kaksi viimeistä matemaattista ilmaisua ovat vivun sääntö. Huomaa, että x_{B -} - X_{B -}^Lens Se on pisteiden C ja D välinen etäisyys; ja x_{B -}^V - X_{B -}, Se on piste D-E: n välinen etäisyys: sitoutumisviivan kaksi puolikkaaa (vipuvarsi).

Tämä yhtälö on hyvin samanlainen kuin se, että kuvataan massat Fulcron kanssa sijaitsevan keinulla:

m₁lens₁ = m₂lens₂

Siten vivusääntö antaa meille mahdollisuuden laskea kokonaismuodot n^Lens ja n^V edellyttäen, että seoksen kokonaismuodot tunnetaan, n_T (n_T = n^Lens + n^V-A.

Toinen muoto

Vivusäännön aikaisempi lauseke aikoo laskea määrät (massat, moolit jne.) tasapainon vaiheista. Vivusäännön tunnetuin versio antaa meille kuitenkin mahdollisuuden laskea kunkin vaiheen fraktiot tai prosenttimäärät ottaen vain etäisyydet x: n välillä_{B -}, X_{B -}^Lens ja x_{B -}^V.

Mieti samaa järjestelmää yllä, jolla on toinen vivusääntö:

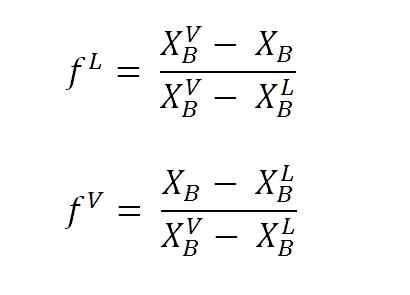Yhtälöt nesteen ja höyryfraktioiden laskemiseksi vipuvarsilla. Lähde: Gabriel Bolívar.

Missä F ^Lens ja F ^VNe ovat vastaavasti molaarisia fraktioita (tai prosenttiosuutta kuvaajasta riippuen) neste- ja höyryfaasista. Huomaa, että ilmeisesti, F ^Lens ja F ^V Heillä ei ole yksiköitä; sillä aikaa n^Lens ja n^V Kyllä, heillä on yksiköt (moolit, grammat jne.-A.

Voi palvella sinua: Reaktiolämpö

Esimerkit

Menetelmä 1

Sekoitetaan säiliössä 28 moolia B ja 12 A: n moolia. Määritä muodostuneiden faasien määrät ja molaariset fraktiot.

Laskemme x_{B -}-

X_{B -} = (28 moolia B)/ (28 moolia B + 12 moolia a)

= 0.7

Tämä arvo vastaa x_{B -} ylimmän kaavion. Kuuntelut antavat meille suunnilleen seuraavat X: n arvot_{B -}^Lens ja x_{B -}^V-

X_{B -}^Lens = 0.41

X_{B -}^V = 0.94

Vivusääntö:

n^Lens(X_{B -} - X_{B -}^Lens) = n^V(X_{B -}^V - X_{B -}-A

Ja tietäen sen n_T = n^Lens + n^V, ja? n_T = 40 moolia, sitten puhdistamme n^Lens jompikumpi n^V toisesta riippuen:

n^Lens(X_{B -} - X_{B -}^Lens) = (40 moolia - n^Lens) (X_{B -}^V - X_{B -}-A

Uudelleenjärjestely ja puhdistus n^Lens meillä tulee olemaan:

n^Lens = (40 moolia) (x_{B -}^V - X_{B -}) / (X_{B -}^V - X_{B -}^Lens-A

Eikö tämä ilmaus muista sitä F ^Lens? Nyt korvaamme, että meillä on:

n^Lens = (40 moolia) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 moolia nestefaasissa

Voimme laskea n^V Kahdella tavalla:

n^V = n^Lens(X_{B -} - X_{B -}^Lens) / (X_{B -}^V - X_{B -}-A

jompikumpi

n^V = 40 moolia - 18.11 Moolia

= 21.89 moolia höyrynvaiheessa

Menetelmä 2

Entä jos lasketaan ensin F ^Lens ja F ^V?

F ^Lens = (X_{B -}^V - X_{B -}) / (X_{B -}^V - X_{B -}^Lens-A

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 tai 45.28%

Eli 45.2% moolista on nestemäisessä vaiheessa, mikä on tämä määrä yhtä suuri kuin:

n^Lens = F ^Lensn_T

= (0.4528) (40 moolia)

= 18.11 Moolia

JA F ^V Voimme laskea sen yhtäläisesti kahdella tavalla:

F ^V = 1 - F ^Lens

jompikumpi

F ^V = (X_{B -} - X_{B -}^Lens) / (X_{B -}^V - X_{B -}^Lens-A

Sen arvo:

F ^V = 0.5472 tai 54.72%

Ja siksi, n^V Se on yhtä suuri kuin:

n^V = F ^Vn_T

= (0.5472) (40 moolia)

= 21.89 Moolia

Huomaa, että vivusäännän kahden muodon soveltaminen vaihtoehtoisina laskentamenetelminä, samat tulokset voidaan saavuttaa. Menetelmä 2 näyttää suoremmalta ja yksinkertaisemmalta; Mutta jos sitä havaitaan huolellisesti, kun raivaus on ratkaistu n^Lens jompikumpi n^V, Nähdään, että molemmat menetelmät ovat todella helppoja.

Ratkaisut

Seuraavaksi ratkaistaan ​​kaksi muuta harjoitusta, joissa nyt tarkasteltaviin järjestelmiin sisältyy neste-kiinteä ja ei-neste-höyry. Myös kaaviot ovat graafisia järjestelmän lämpötilan eikä niiden paineessa.

Harjoitus 1

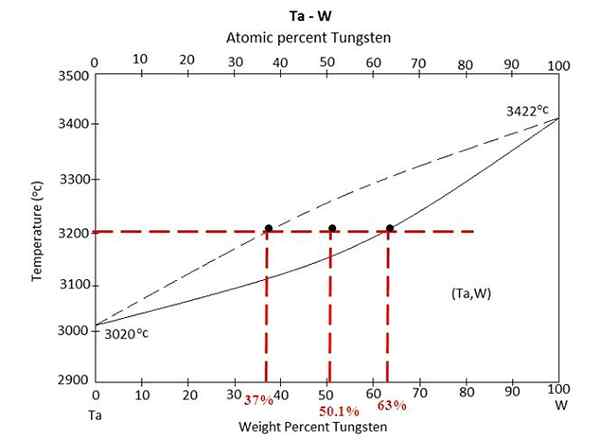Vaihekaavio Tantalon ja volframin välillä. Lähde: Materialspedia, CC BY-SA 4.0, Wikimedia Commons

Meillä on vaihekaavio Tantalon ja volframin välisen seoksen yläpuolella, TA-W. X -akselilla volframin maailmanlaajuiset massaprosentit, W% (m/m) on edustettuna.

Nestemäisen tasapainon alueella (TA+W) ja kiinteä (seos) on seos 3200 ºC: ssa. Määritä kunkin vaiheen massot olettaen, että 100 grammaa seosta kuumennettiin.

Se voi palvella sinua: metallit, ei -metallit ja metalloidit

Menettely

Tällä kertaa harjoitus ratkaistaan ​​vivusäännän toisella muodolla. Unionin linja kertoo meille, että: Kiinteässä vaiheessa meillä on 63% volframista, kun taas nestefaasissa meillä on 37% volframi. Tämä johtuu siitä, että volframi sulaa korkeampaan lämpötilaan (3422 ºC) kuin Tantal (3020 ºC).

Joten meillä on:

W%^S tai w_S= 63%

W%^Lens tai w_Lens= 37%

Ja myös:

W -_{0 -} = 50.1%

Soveltamme vivusääntöä F ^Lens-

F ^Lens = (63% - 50.1%) / (63% - 37%)

= 0.4961 tai 49.61%

Huomaa, että nestefaasia vastaava etäisyys on vipuvarsi lähellä kiinteää vaihetta, keskipisteen vastakkaista puolta.

Nestemäisen faasin massa on siis:

(0.4961) (100 grammaa) = 49.61 sulaa grammaa

Ja kiinteä vaihe on yhtä suuri kuin:

100 grammaa - 49.61 grammaa = 50.39 grammaa seostarikosta, joka on runsaasti volframissa

Harjoitus 2

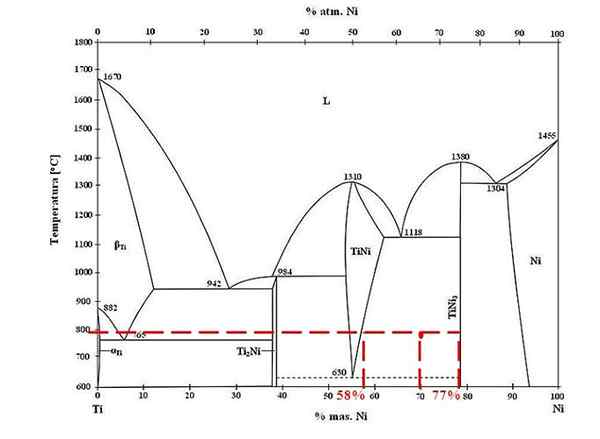Vaihekaavio titaani-nikkeliseoksista. Lähde: Doomgiver, CC BY-SA 3.0, Wikimedia Commons

Titanium- ja nikkeli -seokselle 800 ºC: lla ja 70% nikkelillä määritä kuinka paljon TINI: stä ja Tinistä₃ Ne ovat läsnä.

Menettely

Tällä kertaa he pyytävät vain kunkin vaiheen massajakeita. Punainen piste sijaitsee tasapainoalueella TINI- ja TINI -vaiheiden välillä₃, joiden käyrät ovat siellä, missä se pelaa liiton linjaa, joka virtaa arvoihin 58% tai TINI -vaiheessa, ja 77% tai TINI -vaiheessa₃.

Huomaa, että punainen kohta on lähempänä TINI -vaihetta₃ Tini -vaihe. Tämä tarkoittaa, että Tini on oltava enemmän₃ tuo tini; Ja siksi etäisyys tai vipuvarsi, joka vastaa TINI: tä₃ Sen on oltava pisin, päinvastoin (70%-58%).

Tietäen tämän, jatkamme laskemista F ^Tini3-

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 tai 63.16%

Todellakin, 63.16% seoksesta vastaa TINI -vaihetta₃. Samaan aikaan TINI -vaihe vastaa:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 tai 36.84%

Yhteenvetona kertyneille harjoituksille voidaan sanoa, että vivusääntö on erittäin hyödyllinen kunkin vaiheen fraktioiden määrittämisessä tasapainossa kahden komponentin järjestelmään.

Viitteet

1. Walter J. Moore. (1963). Fysikaalinen kemia. Kemiallisessa kinetiikassa. Neljäs painos, Longmans.
2. Iranin. Levine. (2009). Fysikaalis -periaatteet. Kuudes painos. MC Graw Hill.
3. Wikipedia. (2020). Vivusääntö. Haettu: vuonna.Wikipedia.org
4. Michael Adewumi. (18. toukokuuta 2020). Vivun sääntö. Toipunut: Eng.Librettexts.org
5. Adam Warren. (1997). Vaihekaaviot: Sido linjat ja vivusääntö. Toipunut: Southampton.Ac.Yhdistynyt kuningaskunta
6. Cambridgen yliopisto. (2020). Vivun sääntö. Haettu: DoitPoms.Ac.Yhdistynyt kuningaskunta