Vektorit graafiset tilat

Se Vektorivähennys o vektorien vähennys vektorien välillä tai ja v merkitty tai - v, Se lasketaan lisäämällä vektori tai vastakkaisella vektorilla v. Algebrallisesti vähennys ilmaistaan ​​seuraavasti:

tai - v = tai + (-v-A

Vektoreiden vähentäminen on mahdollista suorittaa erilaisia ​​menettelytapoja, esimerkiksi graafisessa muodossa, tällä tavalla vektori v Se on piirretty suuntautuneella viiva -segmentillä -nuolella-.

Nuolen pituus vastaa vektorimoduulia, tietyn vertailulinjan kallistus - osoittaa suunnan ja pää osoittaa vektorin suunnan.

Vektori vastustaa v Sillä on sama pituus ja suunta, mutta muuten. Sitten ennen vähennystä tai ja v, On välttämätöntä vetää vastakkainen vektori v, ja lisää tämä vektori u.

On erittäin tärkeää korostaa, että vektorien vähentäminen ei ole kommutatiivinen, ts. Vektorien järjestys muuttaa tulosta, siksi:

tai - v ≠ v - tai

Graafinen menettely voidaan suorittaa käyttämällä mitä tahansa näistä menetelmistä, joiden vaiheet selitämme alla:

-Kolmiomenetelmä.

-Rinnakkaisohjelma.

[TOC]

Graafinen vektori sub -grafinen menetelmä

Kolmiomenetelmä

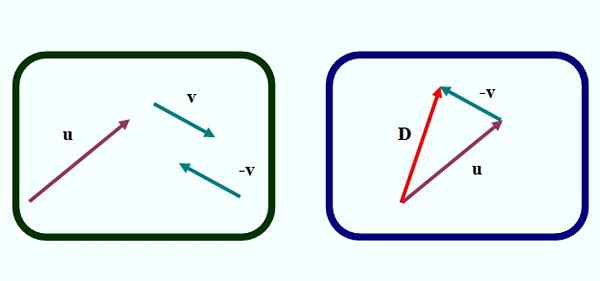
Kuvio 1. Vektorit Subbance triangle -menetelmän mukaisesti. Lähde: f. Zapata.

Kuviossa 1 meillä on ensimmäinen menetelmistä kahden vektorin vähentämiseksi graafisesti. Se on noin Kolmiomenetelmä, Koska vektorien perustamisessa muodostettu luku on kolmio, kuten vasemmassa kuvassa näemme.

Vähentää tai - v Jatkamme seuraavasti:

-Vetää vektori -v Vektorista v, kääntämällä sääntöä ja joukkuetta, mutta nuolen suunnan muuttaminen (vasen kuva).

-Siirtyy vektoriin -v siten, että sen alkuperä osuu samaan aikaan vektorin loppua tai (Oikea kuva).

Voi palvella sinua: kitka: tyypit, kerroin, laskenta, harjoitukset

-Sitten piirretään vektori (punaisella oikeassa kuvassa), joka menee alkuperästä tai lopuksi v. Puhelu D -d Ja se on vektoriero:

D -d = tai - v

Rinnakkaisohjelma

Rinnakkaisogrammimenetelmässä lisäämistä tai vähentämistä koskevien vektoreiden on oltava samat lähtökohdat. Oletetaan, että haluamme löytää tai - v Yllä esitetyillä vektoreilla on vaiheet löytää vektorien vähentäminen tällä menetelmällä ovat seuraavat:

-Määritä päinvastainen vektori v, mikä on -v, kuten aiemmin on kuvattu kolmiomenetelmässä.

-Ota vektorit huolellisesti tai ja -v siten, että sen alkuperän osuu.

-Nyt segmentoidut yhdensuuntaiset viivat on piirretty kunkin vektorin päistä. Muodostunut luku on rinnakkaisogrammi ja erityistapauksissa, joissa vektorit ovat kohtisuorassa, se on suorakulmio tai neliö.

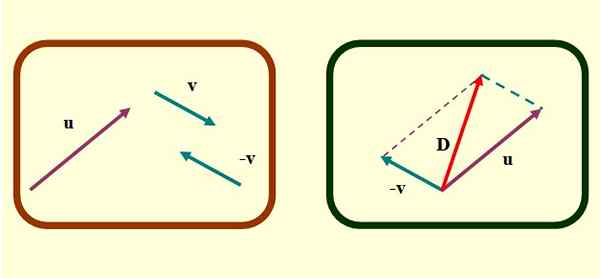Kuva 2. Rinnakkaisogrammimenetelmä vektorivähennystä varten. Lähde: f. Zapata.

-Lopuksi vektori, joka alkaa yhteisestä alkuperästä tai ja v loppuun saakka, missä segmentoidut yhdensuuntaiset viivat on ristissä. Tämä on vektori D -d tai vähennys.

Tärkeä

Toinen tapa tehdä vähennys on piirtää rinnakkaisgrammi ikään kuin haluat lisätä vektoreita.

Mutta sen sijaan Diagonaalinen vastapäätä tai lyhyempiä, Kuten kuvasta nähdään:

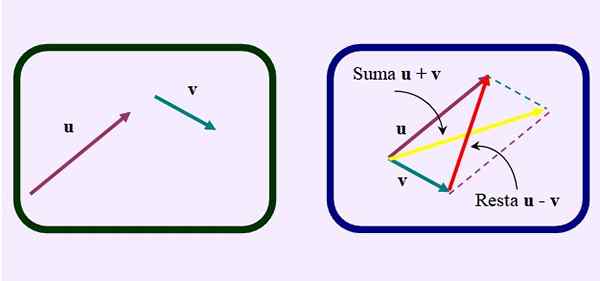Kuva 3. Toinen tapa toteuttaa vektorivähennystä rinnakkaisogrammimenetelmän avulla. Lähde: f. Zapata.

Vektori vähennysesimerkit

- Esimerkki 1

Laiva navigoi joessa ja tekee niin virran vastakkaiseen suuntaan. Maalla tarkkailija huomauttaa, että aluksen nopeus vähenee virran vaikutuksen vuoksi.

Voi palvella sinua: Entä materiaalien sisältämät energiat?

Nopeus on vektori, ja tässä esimerkissä laivan nopeus osoittaa yhteen suuntaan ja virran nopeudella on sama suunta ja vastakkainen suunta. Aluksen nettonopeus on molempien vektorien summa.

Esimerkiksi, jos aluksen instrumentit. Kuten v = v ' +vc, VC: n VC: n nopeus Vähenemisellä V ja V': Vc = V - V '= 30 km/h - 40 km/h = -10 km/ h.

- Esimerkki 2

Elokuvassa meillä on tärkeitä vektoreita, jotka kuvaavat muutoksia:

-Siirtymä aseman muutoksille.

-Keskimääräinen nopeus, kuinka nopeasti sijainti vaihtelee ajassa.

-Kiihtyvyys nopeudenmuutoksille ajan funktiona.

Siirtymävektori

Siirtymävektori kuvaa aseman muutosta, jonka keho kokee liikkeensa aikana.

Katsotaanpa esimerkiksi hiukkanen, joka kuvaa kuviossa esitettyä tasaista etenemissuuntausta, jossa se menee pisteestä P₁ pisteeseen P₂.

X-Y-koordinaattijärjestelmän alkuperästä suunnatut vektorit näihin pisteisiin ovat sijaintivektorit r -₁ ja r -₂, Vaikka siirtymävektori on δr -, p -arvosta₁ P₂. Onko totta että:

Δr - = r -₂ - r -₁

Siksi siirtymävektori on lopullisen sijaintivektorin ja alkuperäisen sijaintivektorin välinen vähennys, kuten seuraavassa kuvassa todetaan. Sen yksiköt ovat myös asennon yksiköitä: metrit, jalat, mailit, senttimetrit ja paljon muuta.

Voi palvella sinua: Perseus (tähdistö): sijainti, mytologia ja ominaisuudet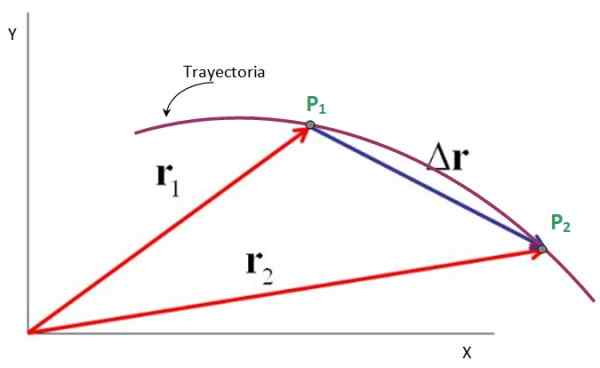Kuva 4. Siirtymävektori on ero lopullisen ja alkuperäisen sijainnin välillä. Lähde: f. Zapata.

Keskimääräinen nopeus ja keskimääräinen kiihtyvyysvektorit

Keskimääräinen nopeusvektori puolestaan v_m Se määritellään siirtymänä kerrottuna aikavälin käänteellä:

 Ja keskimääräinen kiihtyvyys on:

Liikuntaa

Piirin kuvaava hiukkas. In on nopeus v_-Lla = 60 km/h kohti +x- ja b -akselia v_{B -} = 60 km/h kohti +ja. Määritä sen keskimääräinen kiihtyvyys graafisessa ja analyyttisessä muodossa.

Ratkaisu

Graafisessa, keskimääräisen kiihtyvyyden suunnassa ja merkityksessä määritetään:

Seuraava kuva on vähennys v_{B -} - v_-Lla, kolmiomenetelmän kautta keskimääräinen kiihtyvyys -lla_m on verrannollinen δv. Muodostuneessa kolmiossa on kaksi luokkaa yhtä suuret ja siksi akuuttiset sisäkulmat mittaavat 45 º.

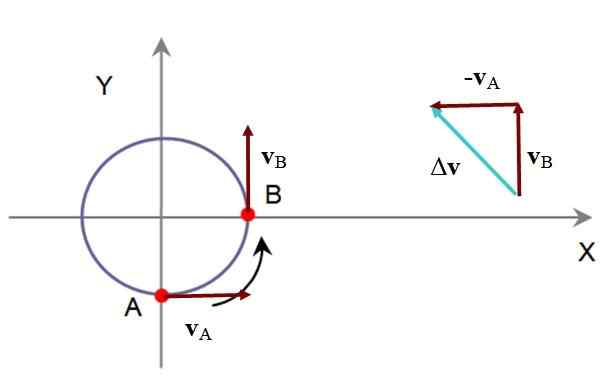Kuva 5. Ratkaistun esimerkin hiukkasten liikkeen kaavio. Lähde: f. Zapata.

Analyyttisesti, jos osoite +x osuu yhteen yksikkövektorin kanssa Yllyttää ja +osoite ja yksikkövektori J -, niin:

Δv = 60 km/h J - - 60 km/h Yllyttää

Lausun tietojen mukaan Δt = 5 s keskimääräinen kiihtyvyys on:

-lla_m = (60 km/h J - - 60 km/h Yo) / 5 s = 12 (J --Yllyttää) Km/(h.s)

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
6. Tipler, P. 2006. Fysiikka tieteen ja tekniikan puolesta. 5. ed. Osa 1. Toimitus palautti.