Suora ja puoliksi reunattu segmentti

Linja- ja puolijärjestelmä erotetaan tosiasiasta, että linjasegmentti on rajoitettu; toisin sanoen heidän alkuperäinen kohta ja päätepiste tunnetaan. Puoli -oikealta tiedetään sen alkupiste, mutta ei sen päätepiste, koska se ulottuu äärettömyyteen.

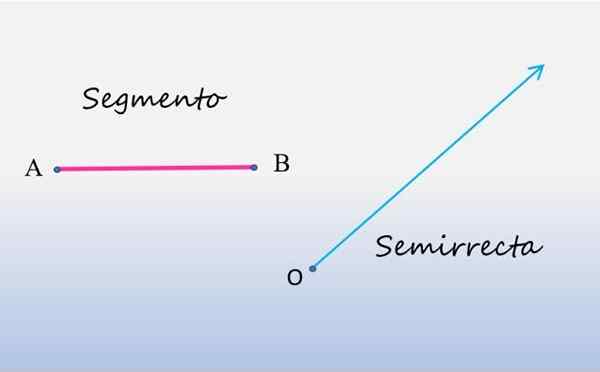
Seuraava kuva näyttää vasemmalla, linjasegmentin ja oikealla puolella -oikealla:

Segmentti ja puoliksi. Lähde: f. Zapata.

Kuten voidaan nähdä, segmentti on viivaviiva, joka alkaa kohdasta A ja päättyy kohtaan B, nämä kohdat ovat mainitun segmentin päät. Segmentin mittaus vastaa sen päiden välillä.

Puoli -oikealla puolella on lähtökohta pisteessä o ja ulottuu äärettömyyteen, mikä vastaa sitä, että sitä rajoitetaan vain yksi pää, yleensä kutsutaan alkuperäisiksi. Tästä syystä niitä kutsutaan myös hyvät taivaat.

Segmentit merkitään kirjaimien kautta, jotka osoittavat alkuperäisen pisteen ja päätä. Esimerkiksi kuvan segmentti on segmentti AB, tai aivohalvaus asetetaan päälle, kuten tämä:

Toisaalta puolivälissä voidaan nimittää myös kahdella kirjaimella, joista toinen osoittaa lähtöä vastaavan pisteen ja toisen ylimääräisen kirjeen. Sitä voidaan käyttää myös pieneen kirjeeseen, joka edustaa salamaa tai puoliksi rekrytointia, ja siellä on myös omalla nimellä puoliksi osittain, kuten esimerkeissä nähdään myöhemmin.

Esimerkkejä segmenteistä

Segmentit ovat erittäin tärkeitä geometriassa, alla on joitain merkittävimpiä:

Monikulmion sivut

Polygonit ovat litteitä ja suljettuja kuvioita, joiden sivut ovat ei -peräkkäisiä linjasegmenttejä. Esimerkiksi kolmiossa on kolme sivua, nelikulmaisella on neljä sivua, viisikulmiossa on viisi ja niin edelleen.

Se voi palvella sinua: Tesseldos: Ominaisuus, tyypit (säännöllinen, epäsäännöllinen), esimerkkejä

Ympärysmitta

Se määritellään se segmentti, joka sisältää kaksi kehän pistettä ja kulkee välttämättä saman keskuksen läpi.

Kehän köysi

Kun segmentti, joka liittyy kehän kahteen pisteeseen.

Kolmion korkeus

Kolmion korkeus määritellään segmentiksi, joka menee kohtisuorasti kolmion sivulta vastakkaiseen kärkeen. Jos kolmion pohjan mitta, nimeltään B ja saman korkeus, nimeltään H h on tiedossa, saman alue A lasketaan hyvin tunnetun kaavan kautta:

A = ½ b ∙ h

Semirret -esimerkit

Puoli -straight ovat myös erittäin tärkeitä elementtejä geometriassa. Joitakin hyvin -tunnetuissa puoliarvoissa ovat:

Positiiviset puolijärjestelmät

Kolme suuntaa avaruudessa: korkea, leveä ja syvyys, voidaan edustaa karteesiakselien järjestelmä, joka koostuu kolmesta molemminpuolisesti kohtisuorasta viivasta toistensa kanssa, merkittynä akselina x, ja ja z -z, jotka leikataan nimeltään kohdassa alkuperä.

Tämä määräys jakaa tilaa kahdeksaan alueelle, joka tunnetaan nimellä Oktaverit. Seuraavassa kuvassa havaitaan positiivisia puoliksi ovia x, ja ja z -z, jotka määrittävät ensimmäisen ocantin. Samoin positiivinen puoliksi -x Y y määrittää nimeltään tason alueen Ensimmäinen kvadrantti.

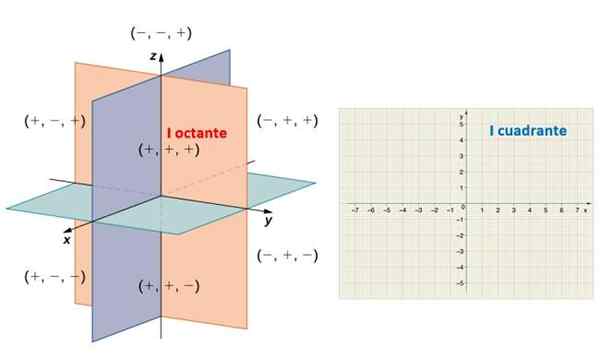Vasemmalla, kahdeksan avaruuden oktaattia ja oikealle, Cartesian kone jaettiin neljään kvadranttiin. Lähde: Math LibretTexts.

Kulman sivut

Kulma on murto -osa tasosta, joka on rajattu kahdella puolijohdassa, jonka alkuperä on yleinen. Tämä kohta on kärki kulmasta, kun taas puoliksi varjosta kutsutaan vastaavasti kulman alku- ja lopullisiksi puoliksi. Tällainen tarjous on esitetty seuraavassa kuvassa:

Se voi palvella sinua: mikä on Rhombus -alueen ja suorakulmion välinen suhde?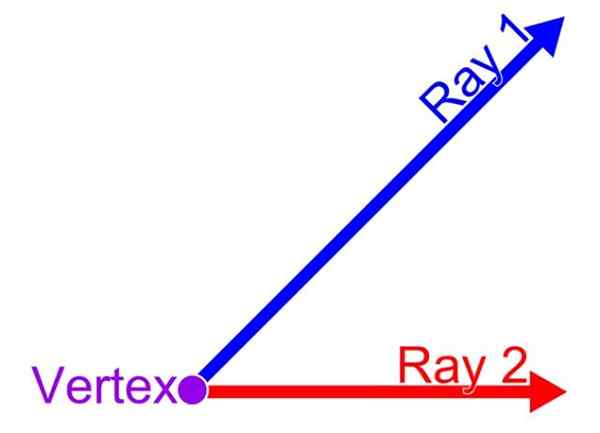 Kulman elementit. Lähde: Wikimedia Commons.