Aksiaalinen symmetriaominaisuudet, esimerkit ja harjoitukset

Se Aksiaalinen symmetria Se tapahtuu, kun kuvan pisteet vastaavat toisen luvun pisteitä suoran mediatrixin avulla, jota kutsutaan symmetria -akseliksi. Sitä kutsutaan myös säteittäiseksi, kierto- tai lieriömäiseksi symmetriaksi.

Sitä käytetään yleensä geometrisissä hahmoissa, mutta se on luonteeltaan helposti havaittavissa, koska on eläimiä, kuten perhosia, skorpioneja, hyllyjä tai kunnolla ihmisiä, jotka esittävät aksiaalisen symmetrian.

Tässä kuvassa Toronton kaupungin horisontista ja sen heijastus veden aksiaalisessa symmetriassa on esillä. (Lähde: Pixabay)

[TOC]

Kuinka löytää symmetrinen aksiaali

P -pisteen symmetrisen aksiaali P ': n löytämiseksi suoritetaan seuraavat geometriset toiminnot suhteessa: L):

1.- Kohtisuorassa linjaan (L) on jäljitetty, joka kulkee pisteen P läpi.

2.- Kahden rivin sieppaaminen määrittää pisteen tai.

3.- PO -segmentin pituus mitataan, sitten tämä pituus kopioidaan linjalle (PO) alkaen p a: n suuntaan tai pisteen P 'määrittäminen.

4.- Piste P.

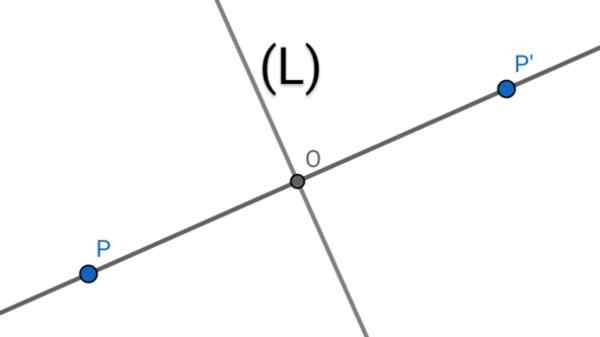Kuvio 1. Kaksi pistettä p ja p 'ovat aksiaalisesti symmetrisiä akselille (l), jos mainittu akseli on PP -segmentin mediatrix'

Aksiaalisen symmetrian ominaisuudet

- Aksiaalinen symmetria on isometrinen, ts. Geometrisen hahmon etäisyydet ja sen vastaava symmetrinen.

- Kulman ja sen symmetrisen mitta on sama.

- Symmetrian akselin symmetrinen aksiaali on itse kohta.

Se voi palvella sinua: Gauss-Seidel-menetelmä: Selitys, sovellukset, esimerkit

- Symmetria -akselin yhdensuuntaisen viivan symmetrinen viiva on myös mainitun akselin suuntainen kioski.

- Symmetria -akselin sekonttiviiva on symmetrinen.

- Linjan symmetrinen kuva on toinen viiva, joka muodostaa kulman saman mittaisen symmetria -akselin kanssa kuin alkuperäisen viivan kuva.

- Symmetrinen symmetrinen kuva, joka on kohtisuorassa symmetrian akselia vastaan, on toinen viiva, joka on päällekkäinen ensimmäinen.

- Viiva ja sen aksiaalinen symmetrinen viiva muodostavat kulman, jonka puolustaja on symmetrian akseli.

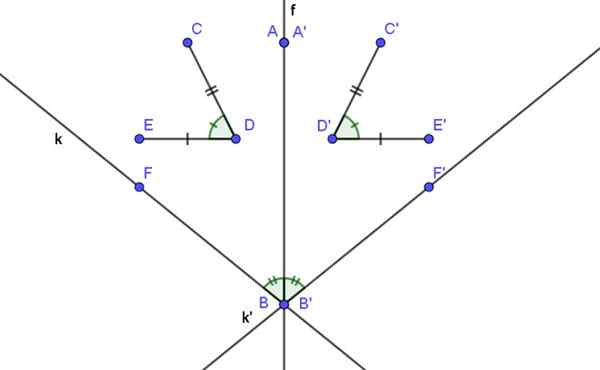Kuva 2. Aksiaalinen symmetria säilyttää etäisyydet ja kulmat.

Esimerkkejä aksiaalisesta symmetriasta

Luonnossa on runsaasti esimerkkejä aksiaalisesta symmetriasta. Esimerkiksi, voit nähdä kasvojen symmetrian, hyönteisten, kuten perhoset, heijastus rauhallisten vesien ja peilien pinnoista tai kasvien lehdistä, muun muassa.

Kuva 3. Tämä perhonen on melkein täydellinen aksiaalinen symmetria. (Lähde: Pixabay) Kuva 4. Tämän tytön kasvoilla on aksiaalinen symmetria. (Lähde: Pixabay)

Aksiaalinen symmetriaharjoitukset

Harjoitus 1

Sinulla on kärkipisteiden A, B ja C kolmio, joiden Cartesian -koordinaatit ovat vastaavasti a = (2, 5), b = (1, 1) ja c = (3,3). Löydä symmetrisen kolmion karteesian koordinaatit y -akselin (ordinaattien akselin) suhteen.

Ratkaisu: Jos pisteessä P on koordinaatit (x, y), niin sen symmetrinen osuuksien akselin suhteen (y akseli) on p '= (-x, y). Toisin sanoen.

Voi palvella sinua: ääretön sarja: Ominaisuudet, esimerkit

Tässä tapauksessa kärjessä olevien symmetrisillä kolmiolla ', B' ja C 'on koordinaatit:

A '= (-2, 5); B '= (-1, 1) ja c' = (-3, 3), kuten voidaan tarkistaa kuvassa 6.

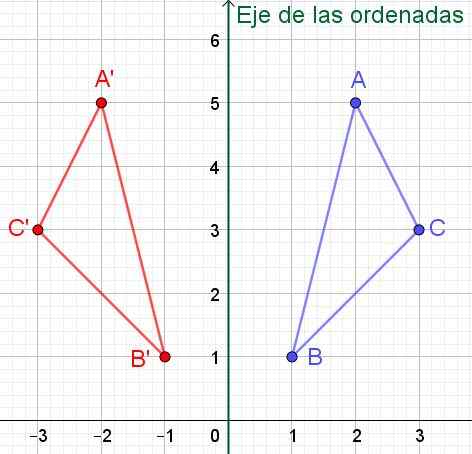Kuva 6. Jos pisteellä on koordinaatit (x, y) sen symmetrinen y-akselin (ordinaattien akselin) suhteen, on koordinaatit (-x, y).

Harjoitus 2

Tarkista, että ABC -kolmioon ja sen symmetriseen A'b'c "-harjoitteluun 1 tarkista, että alkuperäisen kolmion ja sen symmetrisen vastaavilla puolilla on sama pituus.

Ratkaisu: Sivujen etäisyyden tai pituuden löytämiseksi käytämme euklidian etäisyyskaavaa:

d (a, b) = √ ((bx-ax)^2 + (by-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ ((-1 )^2 + (-4)^2) = √ (17) = 4,123

Seuraavaksi lasketaan symmetrisen puolen pituus, joka vastaa'b ': n:

D (a ', b') = √ ((bx'-ax ')^2 +(by'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4,123

Tällä tavalla on todistettu, että aksiaalinen symmetria säilyttää etäisyyden kahden pisteen välillä. Menettely voidaan toistaa kolmion muille puolille ja sen symmetriseksi invarianssin tarkistamiseksi pituudessa. Esimerkiksi | AC | = | A'c '| = √5 = 2 236.

Harjoitus 3

Suhteessa ABC -kolmioon ja sen symmetriseen A'b'c "-harjoitteluun 1 tarkista, että alkuperäisen kolmion ja niiden symmetristen vastaavien kulmien kanssa on sama kulmamittaus.

Ratkaisu: Vektoreiden skalaarituotteiden kulmien ja b'a'c 'mittausten määrittämiseksi lasketaan ensin Ab kanssa Ac ja sitten skalaarituote A'b ' kanssa A'C '.

Muistaa sen:

A = (2, 5), B = (1, 1) ja C = (3,3)

A '= (-2, 5); B '= (-1, 1) ja c' = (-3, 3).

Sinulla on:

Ab = y Ac =

samalla lailla

A'b ' = y Ac =

Voi palvella sinua: Lamy -lause

Sitten löytyy seuraavat skalaarituotteet:

Abteeksiac = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

samalla lailla

A'b'⋅a'c ' = ⋅ = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

BAC -kulman mitta on:

∡Bac = arccos ( Abteeksiac / (|AB |⋅ |AC |)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6º

Samoin kulman mitta b'a'c 'on:

∡B'a'c '= arccos ( A'b'⋅a'c ' / (|A'b '|⋅ |A'C '|)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6º

Päätelmä, että aksiaalinen symmetria säilyttää kulmien mittauksen.

Harjoitus 4

Olla koordinaatin (a, b) piste P. Löydä sen symmetrisen aksiaalin koordinaatit suhteessa linjaan y = x.

Ratkaisu: Kutsumme (A ', B') symmetrisen pisteen P 'koordinaateihin linjan y = x suhteen. Segmentin PP: n 'keskipisteen M

A + A '= B + B'

Toisaalta segmentin PP: n 'on vireillä -1 kohtisuorassa kaltevuuden 1 linjaan y = x, joten seuraava tasa -arvo saavutetaan:

B - b '= a' -a

Kahden yhtäläisyyden puhdistaminen ennen 'ja b' on päätelty, että:

A '= B ja mitä b' = a.

Toisin sanoen pisteen P (a, b), sen symmetrinen aksiaali viivaan y = x on p '(b, a).

Viitteet

1. Arce m., Blázquez S ja muut. Lentokoneen muunnokset. Toipunut: EDUCUTMXLI.Tiedostot.WordPress.com
2. CC -laskenta. Aksiaalinen symmetria. Palautettu: laskelma.DC
3. Superprof. Aksiaalinen symmetria. Toipunut: SuperProf.On
4. Wikipedia. Aksiaalinen symmetria. Palautettu: on.Wikipedia.com
5. Wikipedia. Symmetria pyöreä. Haettu: vuonna.Wikipedia.com