Oktaalijärjestelmä

Mikä on oktaalijärjestelmä?

Hän Oktaalijärjestelmä Se on peruslukujärjestelmä kahdeksan (8); Eli se koostuu kahdeksasta numerosta, jotka ovat: 0, 1, 2, 3, 4, 5, 6 ja 7. Siksi jokaisella oktaalinumeron numerolla voi olla minkä tahansa arvon välillä 0 - 7. Oktaalilukut muodostetaan binaarilukuista.

Tämä johtuu siitä, että sen perusta on tarkka voima kahden (2). Eli oktaalijärjestelmään kuuluvat numerot muodostuvat, kun ne on ryhmitelty kolmeen peräkkäiseen numeroon, jotka on järjestetty oikealta vasemmalle, mikä saa desimaalin arvonsa.

Oktaalijärjestelmän historia

Oktaalijärjestelmällä on alkuperän muinaisina aikoina, kun ihmiset käyttivät kätensä laskeakseen kahdeksan kahdeksan eläintä.

Esimerkiksi lehmien lukumäärän laskemiseksi stabiilissa, oikealla kädellä alkoi peukaloa pienellä sormella; Sitten toisen eläimen laskemiseksi peukalo tuli yhdessä etusormen kanssa ja niin edelleen kunkin käden jäljellä olevilla sormilla, kunnes se valmistuu 8.

On mahdollista, että Oktaalin numerointijärjestelmä ennen desimaalia voidaan laskea interdigitaaliset tilot; toisin sanoen, kerro kaikki sormet lukuun ottamatta peukaloja.

Myöhemmin muodostettiin oktaalien numerointijärjestelmä, joka on peräisin binaarisesta järjestelmästä, koska se tarvitsee monia numeroita vain yhden numeron edustamiseksi; Siitä lähtien luotiin oktaali- ja kuusikulmaiset järjestelmät, jotka eivät vaadi niin monta numeroa ja jotka voivat helposti muuntaa binaariseen järjestelmään.

Oktaalin numerointijärjestelmä

Oktaalijärjestelmä koostuu kahdeksasta numerosta välillä 0 - 7. Näillä on sama arvo kuin desimaalijärjestelmän tapauksessa, mutta niiden suhteellinen arvo muuttuu riippuen siitä, että nämä miehittävät. Kunkin aseman arvo antaa perusvoimat 8.

Se voi palvella sinua: sääntö t: Ominaisuudet, niin että se on esimerkkejä

Numeroiden sijainnissa oktaalilukulla on seuraavat pesot:

8⁴, 8³, 8², 8¹, 8^{0 -}, Oktaalipiste, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Suurin oktaali -numero on 7; Tällä tavalla, kun tässä järjestelmässä lasketaan, numeron sijainti 0: sta 7: een kasvaa. Kun se saavuttaa 7, se kierrätetään 0: een seuraavaa lukua varten; Tämä lisää seuraavaa numeroa. Esimerkiksi sekvenssien laskeminen, oktaalisessa järjestelmässä se on:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

On olemassa perustavanlaatuinen lause, jota sovelletaan oktaalijärjestelmään, ja se ilmaistaan ​​seuraavasti:

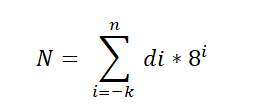
Tässä lausekkeessa DI edustaa numeroa kerrottuna Base 8 -teholla, mikä osoittaa kunkin numeron sijaintiarvon samalla tavalla kuin se on järjestetty desimaalin tarkkuudella.

Esimerkiksi, sinulla on numero 543.2. Jotta se vie sen oktaalijärjestelmään, se hajoaa seuraavasti:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8^{0 -}) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_{d -d}

Tällä tavalla sinulla on 543,2_{Q -} = 354,25_{d -d}. Alaindeksi, joka osoittaa, että se on oktaaliluku, jota voidaan edustaa myös numerolla 8; ja alaindeksi D viittaa desimaalilukuun, joka voidaan myös edustaa numerolla 10.

Oktaalijärjestelmän muuntaminen desimaaliksi

Jotta oktaalijärjestelmän luku on ekvivalentti desimaalijärjestelmään, jokainen oktaalinen numero on kerrottava sen sijaintiarvolla, alkaen oikealta.

Esimerkki 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8^{0 -}) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Voi palvella sinua: matemaattinen tasa -arvo

Esimerkki 2

26.9₈ = (2 _*8¹) + (6_* 8^{0 -}) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1,125

26.9₈= 23 125₁₀

Järjestelmän desimaalimuutos Octaliksi

Desimaalin kokonaisluku voidaan muuntaa oktaalilukuksi käyttämällä toistuvaa jakautumismenetelmää, jossa desimaalin kokonaisluku on jaettu 8: lla, kunnes osamäärä on yhtä suuri kuin 0 ja kunkin jaon jäte edustaa oktaalilukua.

Jätteet tilataan viimeisestä ensimmäiseen; Eli ensimmäinen jäännös on oktaalilukujen vähiten merkittävä numero. Tällä tavoin merkittävin numero on viimeinen jäännös.

Esimerkki

Desimaalin lukumäärä 266₁₀

- Desimaaliluku 266 on jaettu 8 = 266/8 = 33 + 2 Jäännökset.

- Sitten 33 jaetaan 8 = 33/8 = 4 + 1 jäännös.

- 4 on jaettu 8 = 4/8 = 0 + 4 jäännös.

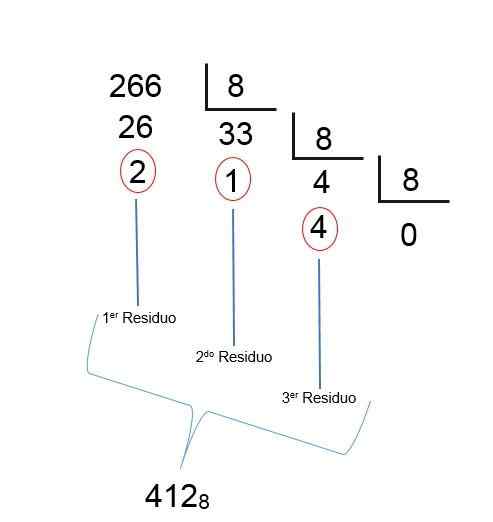
Kuten viimeisen divisioonan A -osamäärä, vähemmän kuin 1 saadaan, se tarkoittaa, että tulos on löydetty; Vain jäännökset on tilattava käänteisesti, niin että desimaalin 266 oktaalimäärä on 412, kuten seuraavassa kuvassa voidaan nähdä:

Binaarinen oktaalijärjestelmän muuntaminen

Oktaalin muuntaminen binaariseksi järjestelmäksi suoritetaan muuntamalla oktaali -numero vastaavaksi binaariseksi numeroksi, joka on muodostettu kolme numeroa. On taulukko, joka osoittaa, kuinka kahdeksasta mahdollisesta numerosta tulee:

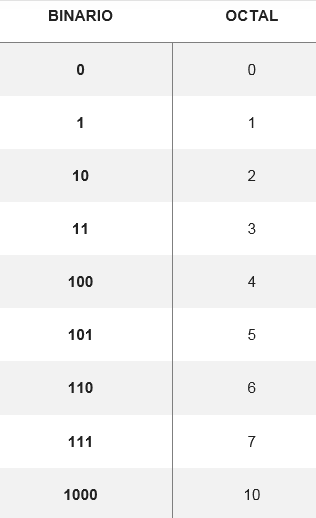
Näistä tuloksista voit muuttaa minkä tahansa määrän oktaalijärjestelmää binaariksi, esimerkiksi muuntaa numero 572₈ Vastaajasi etsitään taulukosta. Siten sinun täytyy:

5₈ = 101

7₈= 111

2₈ = 10

Siksi 572₈ vastaava binaarisessa järjestelmässä 10111110.

Binaarinen järjestelmä oktaalimuunnokseen

Integroitujen lukujen muuntamisprosessi oktaaliksi kokonaislukuiksi on käänteinen toimenpide edelliseen prosessiin.

Voi palvella sinua: mitkä ovat kulman elementit?

Toisin sanoen binaarilukubittit on ryhmitelty kahteen kolmen bitin ryhmään oikealta vasemmalle. Sitten binaarista oktaalista muuntamista tehdään edellisen taulukon kanssa.

Joissakin tapauksissa binaarilukulla ei ole 3 bitin ryhmiä; Suunnitellaan yksi tai kaksi nollaa lisätään ensimmäisen ryhmän vasemmalle puolelle.

Esimerkiksi binaarinumeron 11010110 muuttaminen Oktaalia varten on tehty:

- Kolmen bitin ryhmät muodostetaan oikealta (viimeinen bitti):

11010110

- Koska ensimmäinen ryhmä on epätäydellinen, vasemmalle lisätään nolla:

011010110

- Muuntaminen on tehty taulukosta:

011 = 3

010 = 2

110 = 6

Tällä tavalla binaarinumero 011010110 vastaa 326₈.

Oktaalijärjestelmän muuntaminen heksadesimaaliksi ja päinvastoin

Oktaalilukujen muuttamiseksi heksadesimaaliseksi tai heksadesimaaliksi oktaalijärjestelmään on välttämätöntä, että luku on ensin binaarinen ja sitten haluttu järjestelmä.

Tätä varten on taulukko, jossa jokainen heksadesimaalinumero on edustettuna sen vastaavuudella binaarisessa järjestelmässä, joka koostuu neljästä numerosta.

Joissain tapauksissa binaarilukulla ei ole 4 bitin ryhmiä; Suunnitellaan yksi tai kaksi nollaa lisätään ensimmäisen ryhmän vasemmalle puolelle

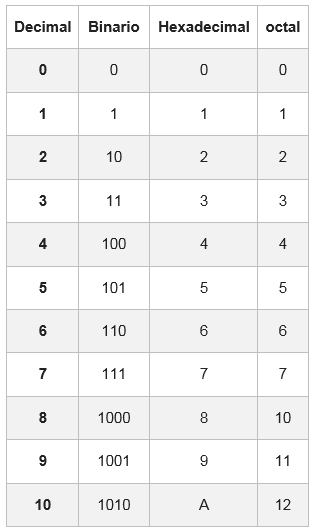
Esimerkki

Muunna 1646 oktaaliluku heksadesimaaliseksi numeroksi:

- Oktaali binaarilukuun tulee

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Siten 1646₈ = 1110100110.

- Muuttaaksesi binaarista heksadesimaaliksi ne on ensin tilattu 4 bitin ryhmään, oikealta vasemmalle:

11 1010 0110

- Ensimmäinen ryhmä on valmis nollalla, jotta siinä voi olla 4 bittiä:

0011 1010 0110

- Heksadesimaalinen binaarisen järjestelmän muuntaminen tehdään. Vastaavuudet korvataan taulukon avulla:

0011 = 3

1010 = a

0110 = 6

Tällä tavoin 1646 oktaaliluku vastaa 3A6: ta heksadesimaalisessa järjestelmässä.