Ne ovat peräsuolen segmenttejä, jotka ovat mahdollisia jokaisessa monikulmiossa

Neliön diagonaali

Strektilineaaliset segmentit, jotka ovat mahdollisia jokaisessa monikulmissa diagonaalit. Diagonaali on linjasegmentti, joka on piirretty yhdistämällä monikulmion kahta ei. Toisin sanoen, diagonaaliset viivat alkavat kuvan kärkipisteestä ja päätyvät toiseen, jota ei ole seuraava.

Yllä olevassa kuvassa neliön diagonaali on esitetty mustana iskuna, joka kuten voidaan nähdä, liittyy kahteen vastakkaiseen kulmaan.

Neliön diagonaalit mittaavat samalla tavalla, mutta rhombuksessa niiden kaksi diagonaalia ovat erilaisia, on suurempi, pidempi ja lyhyempi, lyhyempi.

Kuinka laskea monikulmion diagonaaliluku?

Polygonin diagonaalien lukumäärän määrittäminen voi olla yksinkertaista neliön tai rhombuksen suhteen, mutta kun kuvan sivujen lukumäärä kasvaa, on monimutkaisempaa visualisoida kuinka monta diagonaalia sillä on.

Siksi matematiikassa käytetään yksinkertaista kaavaa, joka tekee tästä prosessista paljon tehokkaamman:

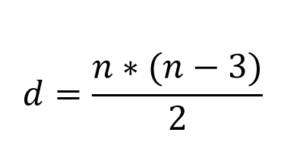
On muistettava, että n on yhtä suuri kuin monikulmion sivujen lukumäärä ja n on aina oltava suurempi kuin 3. Koska? (Jatka lukemista, vastaus on lopussa).

Esimerkki 1

Laske kahdeksankulman diagonaalien määrä.

Kahdeksankulma on säännöllinen kahdeksan puolella oleva monikulmio, tämä tarkoittaa, että kaikki sen sisäiset sivut ja kulmat ovat samat.

Edellisen kaavan avulla se riittää korvaamaan N kahdeksan:

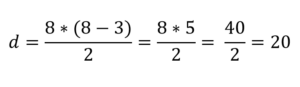
Tällä tavoin tiedetään, että diagonaalien lukumäärä, jotka voidaan piirtää kahdeksankulmaisen monikulmion kärjistä, on 20.

Se voi palvella sinua: Painotetut media: miten se lasketaan, esimerkkejä ja harjoituksia

Ilman kaavaa on todennäköisesti hankala yrittää laskea kaikki diagonaalit, jopa hyvä piirustus. Ja mitä suurempi sivujen sivujen määrä on, sitä monimutkaisempi se on.

Esimerkki 2

Laske suorakulmion diagonaalin pituus Pythagora -lauseen kanssa.

Pythagoras -lause vakuuttaa, että suorakulmiokolmioiden luokkien neliöiden summa, nimeltään A ja B, on yhtä suuri kuin hypotenusen neliö (oikeaa kulmaa vastapäätä olevaa sivua), nimeltään C, nimeltään C.

Algebrallisessa merkinnässä se olisi:

-lla² + b -² = c²

Suorakulmion diagonaali muodostaa suorakulmion kolmion, joka voi käyttää tätä lausetta, missä B on pohja ja H on korkeus.

Jos pohja on 12 cm ja korkeus on 7 cm, sen korvaamisessa on:

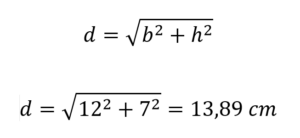
Siksi mainitun suorakulmion diagonaalin pituus on 13,89 senttimetriä.

Monikulmio ilman diagonaaleja

Onko mahdollista, että on olemassa monikulmio, jolla ei ole diagonaalisia viivoja? Kuinka se olisi?

Tätä arvoitusta voidaan käyttää ammuttamaan uteliaisuutta lapsilla ja saamaan heidät visualisoimaan kuvan diagonaalit:

Kolmio on kolmipuolinen monikulmio ja siinä on kolme sisäkulmaa. Mutta siinä ei ole diagonaaleja

Kyllä, kolmiossa ei ole diagonaaleja.

Selitys

Kolmio on kolmipuolinen monikulmio, jolla on kolme sisäkulmaa. Mutta kolmiot ovat kupera lukuja, joissa ei ole diagonaalisia linjoja, jotka ovat yksinkertaisimpia ja kiehtovimpia matematiikan monikulmioita.

Näyttää hyvältä kaavasta, jonka avulla voit laskea monikulmion diagonaalit:

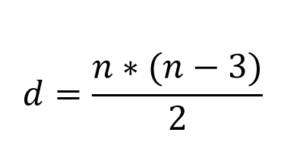
On heti huomattava, että korvaamalla n = 3, se saadaan seurauksena d = 0. Toisin sanoen kolmioissa ei ole diagonaaleja, ei ole mitään keinoa piirtää a. Mutta monikulmioilla, joissa on esimerkiksi n = 4, on kaikki kaksi diagonaalia.

Voi palvella sinua: Decagon: säännöllinen, epäsäännöllinen, ominaisuudet, esimerkit