Eksponentiaalinen pehmenemismenetelmä ja esimerkki

Hän eksponentiaalinen pehmeneminen Se on tapa ennustaa artikkelin kysyntää tietylle ajanjaksolle. Tämä menetelmä arvioi, että kysyntä on yhtä suuri kuin historiallisen kulutuksen keskiarvo tietyllä ajanjaksolla, mikä antaa suuremman painon tai painotuksen arvoille, jotka ovat lähimpiä ajassa. Lisäksi seuraavissa ennusteissa se ottaa huomioon nykyisen ennusteen olemassa olevan virheen.

Kysynnän ennuste on menetelmä projisoida asiakkaiden tuotteen tai palvelun kysyntä. Tämä prosessi on jatkuva, jossa johtajat käyttävät historiallista tietoa laskeakseen, mitä he odottavat olevan tavaran tai palvelun myynnin kysyntä.

Lähde: Pixabay.com

Yrityksen menneisyyden tietoja käytetään lisäämällä se markkinoiden taloudellisiin tietoihin nähdäksesi, kasvaiko myynti.

Kysynnän ennusteen tuloksia käytetään myyntiosaston tavoitteiden asettamiseen yrittäen pysyä yrityksen tavoitteiden mukaisesti.

[TOC]

Eksponentiaalinen pehmenemismenetelmä

Pehmennä on hyvin yleinen tilastollinen prosessi. Pehmennettyä tietoa löytyy usein arjen eri muodoista. Joka kerta kun keskimäärin käytetään kuvaamaan jotain, käytetään pehmeää numeroa.

Oletetaan tänä vuonna lämpimin rekisteröityneet. Sen määrittämiseksi jokaisen tallennetun historiallisen vuoden talvikauden päivittäinen tietojoukko alkaa.

Tämä tuottaa useita numeroita, joilla on suuret "hyppyjä". Tarvitaan joukko, joka eliminoi kaikki nämä tiedot tietoista voidakseen verrata yhden talven toiseen.

Poista datan hyppy kutsutaan pehmentämään. Tässä tapauksessa yksinkertaista keskiarvoa voidaan käyttää pehmeämmän saavuttamiseen.

Voi palvella sinua: EFI Matrix: Mikä arvioi, miten se tehdään, analyysi, esimerkki

Pehmennä ennusteessa

Kysynnän ennusteessa pehmenemistä käytetään myös historiallisen kysynnän variaatioiden poistamiseen. Tämä mahdollistaa kysyntämallien tunnistamisen paremmin, joita voidaan käyttää tulevan kysynnän arviointiin.

Kysynnän vaihtelut ovat sama käsite kuin lämpötilatietojen "hyppy". Yleisin tapa, jolla kysyntähistorian vaihtelut eliminoidaan.

Matkapuhelinkeskiarvo käyttää ennalta määritettyä ajanjaksoa keskiarvon laskemiseksi, ja nämä ajanjaksot liikkuvat ajan myötä.

Esimerkiksi, jos käytetään neljän kuukauden matkapuhelimen keskiarvoa ja tänään on 1. toukokuuta, tammikuussa, helmikuussa, maaliskuussa ja huhtikuussa tapahtuneessa keskimääräisessä kysynnässä käytetään. Käytetään 1. kesäkuuta helmikuun, maaliskuun, huhtikuun ja toukokuun kysyntää.

Painotettu matkaviestin keskiarvo

Kun käytetään yksinkertaista keskiarvoa, tietojoukon jokaiseen arvoon sovelletaan samaa merkitystä. Siksi neljän kuukauden matkapuhelinten keskiarvossa se edustaa joka kuukausi 25% matkapuhelimesta.

Käyttämällä kysyntähistoriaa tulevaisuuden kysynnän projektiin, on loogista päätellä, että viimeisimmällä ajanjaksolla on suurempi vaikutus ennusteeseen.

Mobiilikeskiarvon laskemista voidaan mukauttaa käyttämään erilaisia ​​”pesoja” jokaiselle jaksolle haluttujen tulosten saamiseksi.

Nämä pesot ilmaistaan ​​prosentteina. Kaikkien ajanjaksojen kokonaismäärän on lisättävä 100%.

Siksi, jos haluat soveltaa 35% painona lähimpänä ajanjaksona neljän kuukauden painotetussa keskiarvossa, 35% 100%: sta voidaan vähentää, jolloin 65% jakautuu jäljellä olevien kolmen jakson välillä

Voi palvella sinua: Deming Circle: vaiheet, edut, haitat ja esimerkki

Esimerkiksi, voit päättyä painotuksella 15%, 20%, 30% ja 35% neljän kuukauden ajan (15+20+30+35 = 100).

Eksponentiaalinen pehmeneminen

Eksponentiaalinen pehmenemislaskelman syöttö tunnetaan pehmenemiskerroksena. Edustaa viimeisimmän ajanjakson kysyntään sovellettua painotusta.

Jos 35% käytetään viimeisimmän ajanjakson painotuksena painotetun liikkuvan keskiarvon laskennassa, se voidaan myös valita käyttämään 35% pehmentyneenä tekijänä eksponentiaalisen pehmenemisen laskennassa.

Eksponentiaalinen osa

Ero eksponentiaalisen pehmenemisen laskennassa on, että sen sijaan, että joudut selville, kuinka paljon painoa sovelletaan jokaiseen edelliseen ajanjaksoon, pehmennettyä tekijää käytetään automaattisesti tekemään automaattisesti.

Tämä on "eksponentiaalinen" osa. Jos 35% käytetään pehmennettynä tekijänä, viimeisimmän ajanjakson kysynnän painottaminen on 35%. Ennen viimeisimmän ajanjakson kysynnän painotus on 65% 35%.

65% tulee vähentämällä 35% 100%. Tämä vastaa 22,75%: n painotusta kyseiselle ajanjaksolle. Seuraavan viimeisimmän ajanjakson kysyntä on 65% 65%: sta 35%: sta, mikä vastaa 14,79%.

Edellinen ajanjakso painotetaan 65%: lla 65%: sta 65%: sta 35%: sta, mikä vastaa 9,61%. Tämä tehdään kaikille edellisille jaksoille, kunnes saavut ensimmäisen ajanjakson.

Kaava

Kaava eksponentiaalisen pehmenemisen laskemiseksi on seuraava: (d*s) + (p*(1-s)), missä,

D = kauden uudempi kysyntä.

S = pehmein tekijä, esitetty desimaalisesti (35% olisi 0,35).

P = viimeisimmän ajanjakson ennuste, edellisen ajanjakson pehmenemislaskelman tulos.

Se voi palvella sinua: Nayarit Taloudellinen toiminta

Olettaen, että siellä on 0,35 pehmeän muotoinen tekijä, se olisi sitten: (d*0,35) + (p*0,65).

Kuten voidaan nähdä, ainoat välttämättömät tiedonsiirrot ovat viimeisimmän ajanjakson kysyntä ja ennuste.

Esimerkki

Vakuutusyhtiö on päättänyt laajentaa markkinoitaan maan suurimpaan kaupunkiin tarjoamalla ajoneuvojen vakuutusta.

Alkuperäisenä toimenpiteenä yritys haluaa ennustaa, kuinka monta ajoneuvovakuutusta tämän kaupungin asukkaat ostavat.

Tätä varten he käyttävät alkuperäistietoina toisesta pienemmästä kaupungista ostetun autovakuutuksen määrästä.

Kauden 1 kysynnän ennuste on 2.869 Sopimat ajoneuvovakuutukset, mutta todellinen kysyntä kyseisenä ajanjaksona oli 3.200.

Yhtiön kriteerien mukaan se antaa 0,35 pehmeämmän tekijän. Seuraavan ajanjakson ennustettu kysyntä on: P2 = (3200*0,35) + 2869*(1-0,35) = 2984,85.

Sama laskelma tehtiin koko vuoden ajan, saavuttaen seuraavan vertailevan taulukon kyseisen kuukauden todella saadun ja ennusteen välillä.

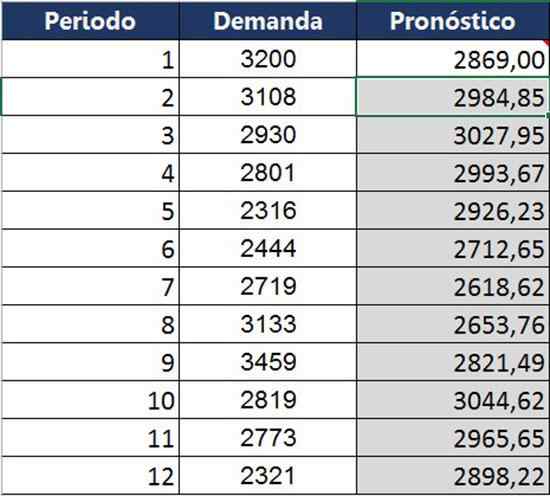
Verrattuna keskiarvoihin eksponentiaalinen pehmeneminen voi ennustaa trendin paremmalla tavalla. Se on kuitenkin edelleen lyhyt, kuten kaaviossa esitetään:

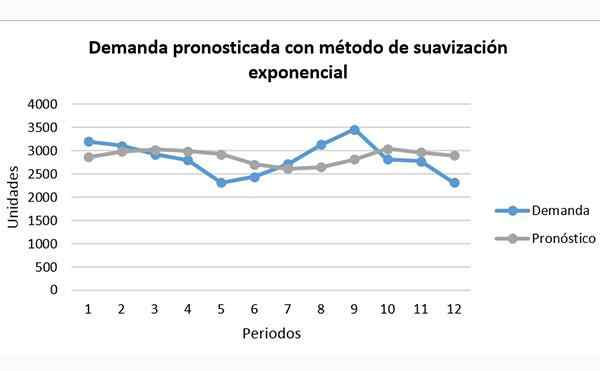
Voit nähdä, kuinka harmaa ennusteviiva löytyy selvästi sinisen kysyntäviivan alapuolelle tai sen yläpuolelle ilman kokonaan.

Viitteet

1. Wikipedia (2019). Eksponentiaalinen pehmeneminen. Otettu: se on.Wikipedia.org.
2. Työllisyys Ingenio (2016). Kuinka käyttää yksinkertaista eksponentiaalista pehmeyttämistä kysynnän ennustamiseen. Otettu: IngenioEmpresa.com.
3. Dave Piacki (2019). Eksponentiaalinen tasoitus selitetty. Otettu: Inventoryps.com.
4. Tutkimus (2019). Kysynnän ennustetekniikat: Avege ja Exponentiaalinen tasoitus. Otettu: Opiskelu.com.
5. CityU (2019). Eksponentiaaliset tasoitusmenetelmät. Otettu: Henkilökohtainen.Cb.Kaupunki.Edu.HK.