Bolzano -lause

Selitämme, mikä Bolzanon lause on, sen sovellukset ja panostetut harjoitukset

Mikä on Bolzanon lause?

Hän Bolzano -lause Se osoittaa, että jos funktio on jatkuvaa suljetun aikavälin [a, b] kaikissa kohdissa, ja on täytetty, että ”A” ja “B” (funktion alla) kuvassa on vastakkaisia ​​merkkejä, niin ainakin on ainakin Yksi kohta "C" avoimessa aikavälillä (A, B), niin että "C" -toiminto on yhtä suuri kuin 0.

Tämän lauseen totesi filosofi, teologi ja matemaatikko Bernard Bolzano vuonna 1850. Tämä tutkija, syntynyt nykyisessä Tšekin tasavallassa, oli yksi ensimmäisistä historian matematiikoista, joka esitteli muodollisen jatkuvien toimintojen ominaisuudet.

Selitys lauseesta

Bolzanon lause tunnetaan myös välituotteiden arvona, joka auttaa määrittämään tiettyjen todellisen muuttujan tiettyjen todellisten toimintojen erityiset arvot, erityisesti nollat.

Tietyssä funktiossa f (x) jatkuu -eli f (a) ja f (b) on kytketty käyrällä, missä f (a) on x -akselin alapuolella (on negatiivinen) ja f (b) X -akselin yläpuolelle (se on positiivinen) tai päinvastoin, X -akselilla on leikkauspiste, joka edustaa väliarvoa "C", joka on välissä "A" ja "B", ja arvon ja arvon välillä f (c) se on yhtä suuri kuin 0.

Kun analysoidaan graafisesti Bolzanon lause, voidaan tietää, että jokaiselle jatkuville F -toiminnoille, jotka on määritelty aikavälillä [a, b], missä F (a)_*f (b) on alle 0, kyseisen toiminnon sisällä on ainakin yksi juuri “c” väliaikalla (a, b).

Tämä lause ei määritä siinä avoimessa aikavälillä olevien pisteiden lukumäärää, siinä todetaan vain, että on ainakin yksi piste.

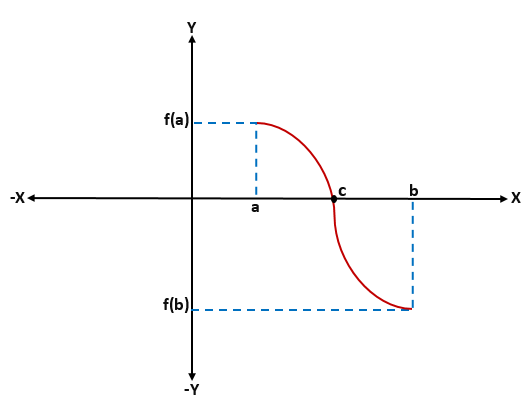
Bolzano -lauseen esittely

Bolzanon lauseen osoittamiseksi oletetaan menettämättä yleisyyttä, että f (a) 0; Tällä tavoin "A" ja "B" välillä voi olla monia arvoja, joille f (x) = 0, mutta on tarpeen vain osoittaa, että yksi on yksi.

Voi palvella sinua: kuvitteelliset numerot: Ominaisuudet, sovellukset, esimerkit

Se alkaa arvioida F keskipisteessä (A+B)/2. Jos f ((a+b)/2) = 0, testi päättyy tähän; Muutoin sitten F ((A+B)/2) on positiivinen tai negatiivinen.

Yksi aikavälin [a, b] puolikkaista on valittu siten, että päissä arvioidun funktion merkit ovat erilaisia. Tämä uusi aika on [A1, B1].

Nyt, jos f arvioidaan [A1, B1] keskipisteessä, ei ole nolla, sama operaatio suoritetaan ennen; Toisin sanoen puolet tästä aikavälistä, joka vastaa merkintöjen kuntoa. Ole tämä uusi aikaväli [A2, B2].

Jos tämä prosessi jatkuu, niin on olemassa kaksi peräkkäistä an ja bn, niin että:

an kasvaa ja bn vähenee:

a ≤ a1 ≤ a2 ≤ ... ≤ an .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Jos kunkin aikavälin pituus [AI, BI] lasketaan, sinun on:

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

.. .

bn-an = (b-a)/2^n.

Siksi raja, kun N: llä on taipumus äärettömyyteen (bn-an), on yhtä suuri kuin 0.

Tämän an: n käyttäminen kasvaa ja rajoitettua ja bn on vähenevä ja rajoitettu, on arvo "C" siten, että:

a ≤ a1 ≤ a2 ≤ ... ≤ an .. .≤ c ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Lim -raja on "C" ja bn raja on myös "c". Siksi, kun kaikki Δ> 0, on aina ”n” siten, että aikaväli [an, bn] sisältyy aikaväliin (c-Δ, c+Δ).

Nyt on osoitettava, että f (c) = 0.

Jos f (c)> 0, niin kuin f on jatkuva, on ε> 0, että F on positiivinen koko aikavälin (c -ε, c+ε). Kuten edellä todettiin, on kuitenkin ”n” -arvo siten, että f muuttaa kirjautumista [An, BN] ja lisäksi [An, BN] sisältyy (c -ε, c+ε), mikä on mitä on ristiriita.

Jos f (c) 0 sellainen, että f on negatiivinen koko aikavälin ajan (c -ε, c+ε); Mutta on "n" -arvo, joka F: n muutos muuttuu [An, Bn]. Osoittautuu, että [an, bn] sisältyy (c -ε, c+ε), joka on myös ristiriita.

Voi palvella sinua: ryhmittelyn merkkejä

Siksi f (c) = 0 ja tämä halusi osoittaa.

Mikä on Bolzano -lause?

Graafisesta tulkinnastaan ​​Bolzanon lausetta käytetään juurten tai nollan löytämiseen jatkuvasta toiminnosta bisentin kautta (lähestymistapa), joka on inkrementaalinen hakumenetelmä, joka jakaa väliajat aina kahteen.

Siten, jos funktio muuttaa allekirjoituksen väliin, F -funktio arvioidaan keskipisteessä, joka ilmaistaan ​​seuraavasti: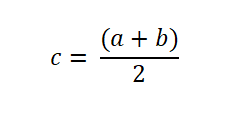Juuri löytyy, kun f (c) = 0. Jos ei, f (c) -merkkiä analysoidaan sen määrittämiseksi, onko se vastustaa f (a): n merkkiä tai f (b).

Sitten kuluu aika [a, c] tai [c, b], missä merkin muutos tapahtuu, ja prosessi toistetaan, kunnes aikaväli on vähemmän ja vähemmän lähestyäksesi haluamaasi arvoa; eli arvoon, jonka funktio on 0.

Yhteenvetona voidaan todeta, että Bolzano -lauseen soveltamiseksi ja juuret löytävät siten rajoittamalla funktion nollia tai anna ratkaisu yhtälöön, seuraavat vaiheet:

1. Se varmistetaan, jos F on jatkuva funktio aikavälillä [a, b].
2. Jos väliä ei anneta, on löydettävä sellainen, jossa funktio on jatkuvaa.
3. Se varmistetaan, jos aikavälin päät antavat vastakkaisia ​​merkkejä, kun ne arvioidaan F: ssä.
4. Jos vastakkaisia ​​merkkejä ei saatu, aika on jaettava kahteen osa -alueeseen käyttämällä keskipistettä.
5. Arvioi funktio keskipisteessä ja tarkista, että Bolzano -hypoteesi täyttyy, missä F (A) _* f (b) < 0.
6. Arvon merkistä (positiivinen tai negatiivinen) riippuen prosessi toistetaan uudella subintervalia, kunnes mainittu hypoteesi täyttyy.

Voi palvella sinua: epälineaarinen ohjelmointi: menetelmät ja harjoitukset

Ratkaisut

Harjoitus 1

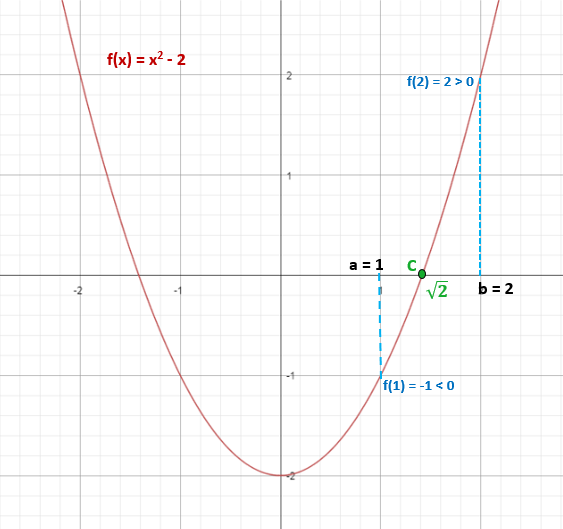
Määritä, onko funktio f (x) = x² - 2, on ainakin yksi todellinen ratkaisu aikavälillä [1,2].

Ratkaisu

Sinulla on funktio f (x) = x² - 2. Kuten polynomi, se tarkoittaa, että se on jatkuvaa millä tahansa aikavälillä.

Pyydetään selvittämään, onko sillä todellinen ratkaisu aikavälillä [1, 2], joten nyt sinun on vain vaihdettava toimintojen välin päät tietääksesi näiden merkki ja tiedettävä, vastaavatko ne olemisen ehdon eri:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negatiivinen)

f (2) = 2² - 2 = 2 (positiivinen)

Siksi merkki f (1) ≠ merkki f (2).

Tämä varmistaa, että on ainakin yksi piste “C”, joka kuuluu aikaväliin [1,2], jossa f (c) = 0.

Tässä tapauksessa C -arvo voidaan laskea helposti seuraavasti:

x² - 2 = 0

x = ± √2.

Siten √2 ≈ 1,4 kuuluu aikaväliin [1,2] ja täyttää F (√2) = 0.

Harjoitus 2

Osoita, että yhtälö x⁵ + x + 1 = 0: lla on vähintään yksi todellinen ratkaisu.

Ratkaisu

Ensin huomaamme, että f (x) = x⁵ + X + 1 on polynomifunktio, mikä tarkoittaa, että se on jatkuvaa kaikissa todellisissa määrissä.

Tässä tapauksessa ei anneta väliä, joten sinun on valittava arvot intuitiivisesti, mieluiten lähellä 0, arvioidaksesi funktiota ja löydettävä merkin muutokset:

Jos käytetään väliä [0, 1], sen on:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Koska merkkejä muutosta ei ole, prosessi toistetaan toisella aikavälillä.

Jos käytetään väliä [-1, 0], sinun on:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

Tällä aikavälillä on merkin muutos: merkki f (-1) ≠ f (0) -merkki, mikä tarkoittaa, että funktio f (x) = x⁵ + X + 1: llä on vähintään yksi todellinen juuri “C” intervallissa [-1, 0], niin että f (c) = 0. Toisin sanoen on totta, että x⁵ + x + 1 = 0: lla on todellinen ratkaisu aikavälillä [-1,0].