Miletus sellainen lause

Selitämme tällaisen ensimmäisen ja toisen lauseen, esimerkkejä ja harjoituksia ratkaistaan

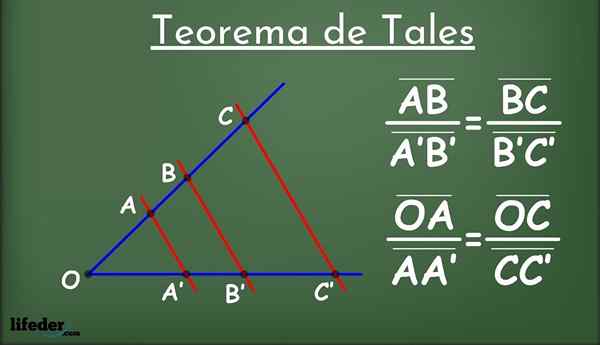
Kuvio 1.- Tales -lause

Mikä on sellainen?

Hän sellainen lause Miletuksesta hän todella viittaa useisiin geometrian lauseisiin, jotka on omistettu Miletus -muinaisten Kreikan thales -viisaille, jotka asuivat 624: stä 546: e.

Matemaatikon ja geometrin lisäksi sellainen oli filosofi, joka tunnustettiin hänen suuresta terävyydestään. Sanotaan, että hän onnistui mittaamaan suuren pyramidin korkeuden käyttämällä yhtä sen lausetta.

Hän Ensimmäinen lause Se viittaa segmenteihin, joita rinnakkaiset viivat määräävät kahdessa viivalta tasolla. Nämä segmentit pitävät suhteellisuussuhdetta, kuten pian nähdään, mikä ulotetaan kahden kolmion sivuille, edellyttäen, että tietyt olosuhteet täyttyvät.

Tämä lause on käytännössä erittäin hyödyllinen, koska se mahdollistaa erittäin korkean tai vaikean pääsyn rakenteiden korkeuden määrittämisen ilman tarvetta mitata niitä suoraan. Juuri juuri mitä tarinat tekivät, kun hän mittasi suuren pyramidin korkeuden.

Puolestaan Tämän toisen lauseen Linkkipisteet, jotka kuuluvat ympärysmittaan, jossa on rekisteröity suorakulmio kolmio, jonka hypotenuse osuu sen halkaisijan kanssa.

Ensimmäinen lause

Olla kaksi linjaa tasossa, nimeltään l₁ ja minä₂ (Kuviossa 1 sinisellä) ja ryhmän linjoja, jotka ovat yhdensuuntaisia ​​toistensa kanssa (punaisella), jotka leikkaavat L: n₁ ja minä₂.

Rinnakkaiset viivat jakavat viivat segmentteihin l₁ ja minä₂: Ab, a'b ', bc, b'c' ja niin edelleen. Segmenttien joukossa luodaan seuraava suhteellisuussuhde:

Esimerkiksi tässä kuvassa ”X” -segmentin mitta on laskettu sellaisen lauseen avulla, koska viivat leikkaavat useat rinnakkaiset, jotka määrittävät segmentit, joilla on tunnettu pituus:

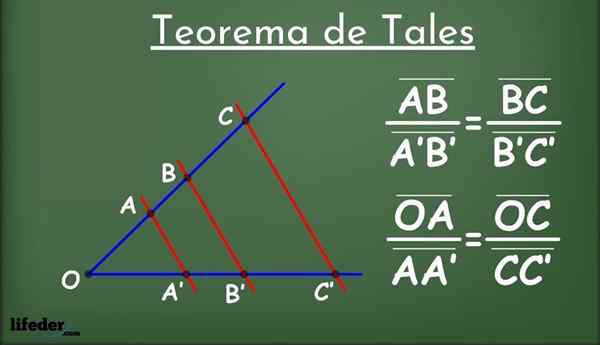
Se voi palvella sinua: toisiaan poissulkevat tapahtumat: ominaisuudet ja esimerkitKuva 2.- Ensimmäisen tällaisen lauseen soveltaminen segmentin X mittauksen määrittämiseksi. Lähde: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Tällainen lause vastaaville kolmioille

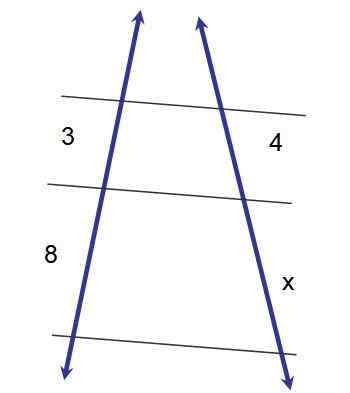
Lause voidaan laajentaa kolmioihin seuraavasti: Oletetaan, että ABC. Tällä tavoin saadaan kaksi samanlaista kolmiota: ABC ja DEC, joiden sisäiset kulmat ovat yhdenmukaisia, ts. Niillä on yhtä suuri mitta.

Kuva 3.- Kaksi kolmiota sellaisen asennossa, kahdella rinnakkaisella sivulla ja yhteinen kulma, ovat samanlaisia. Lähde: f. Zapata.

Kun tällä tavalla järjestetään kaksi kolmiota, sanotaan, että ne ovat sellaisessa asennossa.

Segmenttien välinen suhteellinen suhde nostetaan samalla tavalla kuin rinnakkaisilla viivoilla:

Joka vastaa tätä toista, kunkin kolmion vastaavien puolten välillä, joita kutsutaan myös homologisiksi puoliksi:

Jokaista näistä osuuksista kutsutaan samankaltaisuus. Samankaltaisissa kolmioissa syynä samankaltaisuuteen on yhtä suuri kuin kehän ja samankaltaisuussuhteen neliön välinen osoitus on yhtä suuri kuin alueiden välinen osuus.

Seuraavaksi esimerkki, jossa tällaista lausetta voidaan soveltaa samanlaisiin kolmioihin ja selvittää, kuinka paljon tuntematon puoli X on arvoinen.

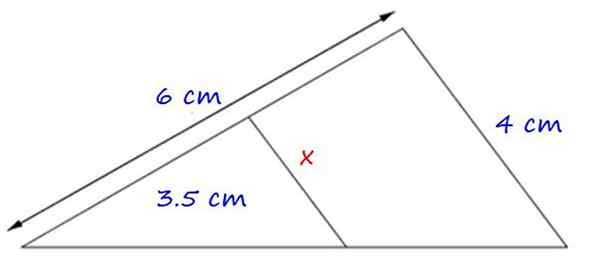Kuva 4.- Sovellusesimerkki ensimmäisestä tällaisesta lauseesta. Lähde: f. Zapata.

Muodostuneet kolmiot ovat samanlaisia, koska niillä on yhteinen kulma ja sivut x ja 4 cm ovat yhdensuuntaiset.

Siksi vastaavien sivujen välinen suhteellisuus on:

Ja X: n arvo tyhjennetään helposti:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Tämän toisen lauseen

Tämä lause viittaa kolmioon, jonka kärkipisteet ovat kohtia, jotka kuuluvat ympärysmittaan, mikä tarkoittaa, että se on rekisteröity siihen.

Tässä tapauksessa lause osoittaa, että aina kun hypotenusa vastaa kehän halkaisijaa, siten jäljitetty kolmio on suorakulmio, ts. Yksi sen sisäkulmista mittaa 90º, kuten kuvassa 5 vasemmalla vasemmalla.

Voi palvella sinua: Ilmaisujen symbolointi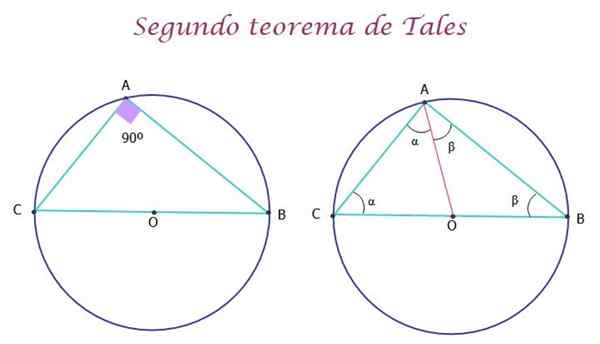Kuva 5.- Tällaisten toisten toisten lauseiden toinen lause, että kehässä rekisteröity kolmio on suorakulmio. Lähde: f. Zapata.

Tällaisen toisen lauseen osoittaminen

Lauseen osoittaminen on hyvin yksinkertaista. Yllä olevassa kuvassa AO -segmentti on piirretty punaisella, muodostamaan kaksi AOC- ja AOB -kolmiota, jotka ovat tasa -arvoisia, koska sivut OA, OC ja OB ovat kehän radioita ja siksi ne mittaavat saman.

Tällä tavoin kolmioilla on kaksi yhtä suurta kulmaa, jotka ovat vastaavasti α ja β. Nyt alkuperäisen ABC -kolmion kohdalla, kuten minkä tahansa kolmion kohdalla, on täytettävä, että sen sisäisten kulmien mittojen summa on yhtä suuri kuin 180º, siksi:

α + (α + β) + β = 180º

Siten:

2α + 2β = 180º

Siksi:

2 (α +β) = 180º

α +β = 90º

Mikä todistaa, että ABC -kolmion sisäkulma on 90º ja siksi se on oikea kolmio.

Esimerkki

Seuraavassa kuvassa kolmio ABC on sammutus ja suorakulmio (isorectangle kolmio), ja se on kehän kehä, joka on yhtä suuri kuin 25 cm. Kuinka paljon AC- ja AB -segmentit ovat?

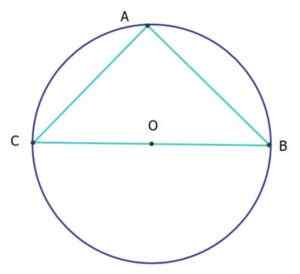
Ympyrän kehä on sen pituus l, joka on annettu sen halkaisijan D mukaan riippuen kaavan avulla:

L = πd

Siksi halkaisija, joka on CB -segmentti, mittaa:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Koska kolmio on samoitus, tämä tarkoittaa, että sen akuuttiset kulmat mittaavat kukin 45º. Koska kolmion hypotenuse on kehän halkaisija, voidaan käyttää trigonometristä suhdetta 45, esimerkiksi:

SEN 45º = AC/CB

Ac = cb × sin 45º = 7.96 cm × sin 45º = 5.64 cm

Voi palvella sinua: Moivre -lause

AB -puolella on sama mitta: 5.64 cm, koska kolmio on samanakasta.

Tällaiset lausekeskukset

Ensimmäistä tällaista lausetta voidaan käyttää tietämään etäisyyksiä, jotka eivät ole helposti mitattavissa. Sanotaan.

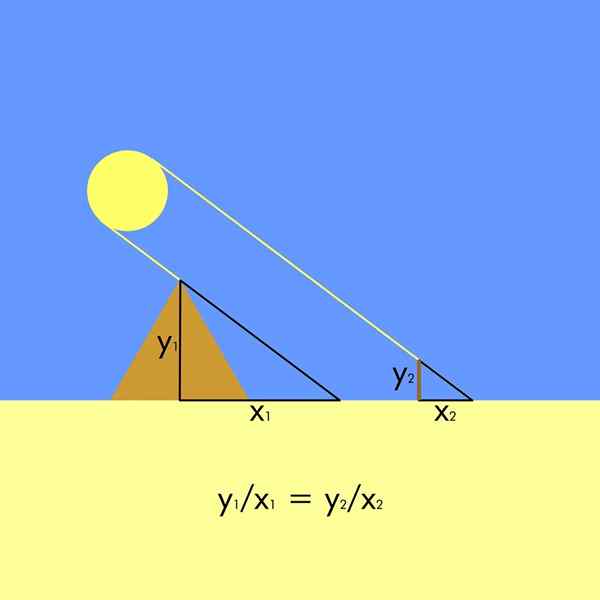
Tätä varten se oli välttämätöntä. Siten muodostuu kaksi samanlaista kolmiota, koska auringonsäteillä on samansuuntainen esiintyvyys.

Kuvassa pyramidin korkeus on ja₁ Ja hänen varjo on x₁, Vaikka vaarnan korkeus on ja₂ (Jotkut kroonikot väittävät, että sellainen käytti omaa korkeuttaan) ja heidän varjonsa on x₂. Koska kolmiot ovat samanlaisia, muodostuu seuraava suhteellisuussuhde:

On erittäin helppo puhdistaa pyramidin korkeus ja₁-

ja₁ = x₁∙ (ja₂ ÷ x₂-A

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Requena, b. Sellainen lause. Toipunut: UniversOformulat.com.
3. Matemaattinen salissa. Tales de Mileto ja suuri pyramidi. Haettu: Salonmatematic.com
4. Superprof didaktinen materiaali. Miletus sellainen. Toipunut: SuperProf.On.
5. Thales ja samankaltaisuuslause. Kaksi hyvin vanhaa ongelmaa. Palautettu: Edu.Xunta.Gal.