Fyysinen

Torricelli -lause

Torricelli -lause

Mikä on Torricellin lause?

Hän Torricelli -lause o Torricelli -periaatteessa todetaan, että säiliön tai säiliön seinämän reiän läpi tulevan nesteen nopeus on identtinen, jonka kanssa esine hankkii, joka pudotetaan vapaasti nesteen vapaan pinnan korkeudesta Reikä.

Lause on havainnollistettu seuraavassa kuvassa:

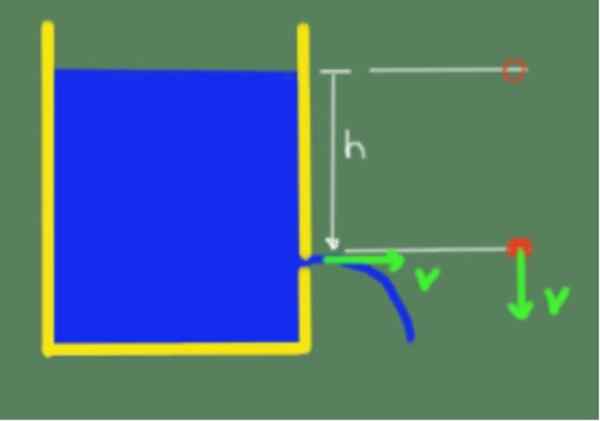Esimerkki Torricellin lauseesta. Lähde: Itse tehty.

Torricellin lauseen takia voimme sitten sanoa, että nesteen ulostulon nopeus reikällä, joka on korkeudella h nesteen vapaan pinnan alapuolella, annetaan seuraavalla kaavalla:

Missä G on painovoiman kiihtyvyys ja H on korkeus reikästä nesteen vapaaseen pintaan.

Evankelista Torricelli oli fyysinen ja matemaatikko, joka syntyi Faenzan kaupungissa, Italia vuonna 1608. Torricelli johtuu elohopeabarometrin keksinnöstä, ja tunnustuksena on paineyksikkö nimeltään “Torr”, mikä vastaa elohopean millimetriä (mm Hg).

Lauseen osoitus

Torricellin lauseessa ja nopeuden antavan kaavan mukaan se olettaa, että viskositeetista aiheutuvat tappiot ovat halveksittavia, kuten vapaassa pudotuksessa oletetaan, että kitka johtuen ilman putoamisesta käyneestä ilmasta on merkityksetön.

Aikaisempi oletus on kohtuullinen useimmissa tapauksissa ja merkitsee myös mekaanisen energian säilyttämistä.

Lauseen osoittamiseksi löydämme ensinnäkin nopeuskaavan objektille, joka vapautuu nolla alkuperäisellä nopeudella, samasta korkeudesta kuin säiliön nesteen pinta.

Voi palvella sinua: Kolmen dimensionaaliset aallot: konsepti, tyypit ja esimerkit

Energian säilyttämisperiaatetta sovelletaan sen kohteen nopeuden saamiseksi, joka putoaa juuri kun korkeus on pudonnut h yhtä suuri kuin reiästä vapaaseen pintaan.

Koska kitkahäviöitä ei ole, on pätevää soveltaa mekaanisen energian säilyttämisen periaatetta. Oletetaan.

Esine, joka putoaa

Kun esine vapautuu nesteen vapaan pinnan korkeudesta, sen energia on vain gravitaatiopotentiaalia, koska sen nopeus on nolla ja siksi sen kineettinen energia on nolla. Potentiaalinen energia -EP on annettu:

EP = M G H

Kun se menee reiän eteen, sen korkeus on nolla, potentiaalienergia on nolla, joten siinä on vain kineettinen energia EY: Annetaan:

EC = ½ m v2

Koska energia säilyy EP = EC: n suhteen:

½ m v2 = m g h

Nopeuden puhdistaminen v Sitten saadaan Torricelli -kaava:

Neste, joka tulee ulos reikästä

Seuraavaksi löydämme nesteen ulostulon nopeuden reiän läpi osoittaaksemme, että se on samanaikainen sen kanssa, joka on juuri laskettu esineelle, joka putoaa vapaasti.

Tätä varten luotamme Bernoulli -periaatteeseen, joka ei ole muuta kuin nesteisiin sovelletun energian säilyttämistä.

Bernoullin periaate on muotoiltu näin:

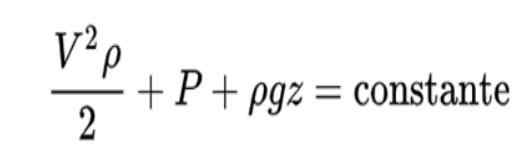
Tämän kaavan tulkinta on seuraava:

  • Ensimmäinen termi edustaa nesteen kineettistä energiaa tilavuusyksikköä kohti
  • Toinen edustaa paineen tekemää työtä poikittaisen alueen yksikköä kohti
  • Kolmas edustaa gravitaatiopotentiaalienergiaa nesteen tilavuuden yksikköä kohti.
Voi palvella sinua: hetkellinen nopeus: Määritelmä, kaava, laskenta ja harjoitukset

Kun aloitamme lähtökohdasta, joka on ihanteellinen neste, ei -tahdissa olevissa olosuhteissa, joissa on suhteellisen alhaiset nopeudet, niin on aiheellista vakuuttaa, että nesteen yksikkömäärän mekaaninen energia yksikköä kohti on vakio kaikilla saman alueilla tai poikittaisosissa.

Tässä kaavassa V on nesteen nopeus, ρ Nestetiheys, P Paine ja z -z Pystysuora sijainti.

Seuraavassa kuvassa Torricellin kaava osoitetaan Bernoulli -periaatteen perusteella.

Levitämme Bernoulli -kaavan nesteen vapaaseen pintaan, jota me osoitamme (1) ja lähtöreiässä, jota merkitsemme (2). Nollakorkeus on valittu lähtöreiän kanssa.

Ei olettaa, että (1): n poikkileikkaus on paljon suurempi kuin kohdassa (2), voidaan sitten olettaa, että nesteen vähenemisen nopeus kohdassa (1) on käytännössä jätetty.

Siksi v on sijoitettu1= 0, paine, johon neste kohdistuu kohdassa (1), on ilmakehän paine ja reikästä mitattu korkeus on h.

Lähtöosassa (2) oletamme, että lähtönopeus on V, paine, johon neste poistoan kohdistuu, on ilmakehän paine ja lähtökorkeus on nolla.

Osat (1) ja (2) vastaavat arvot korvataan Bernoulli -kaavassa ja yhtä suuret. Tasa -arvo on pätevä, koska oletamme, että neste on ihanteellinen ja viskoosisia kitkahäviöitä ei ole. Kun kaikki termit on yksinkertaistettu, nopeus saadaan lähtöreiästä.

Voi palvella sinua: Punainen kääpiö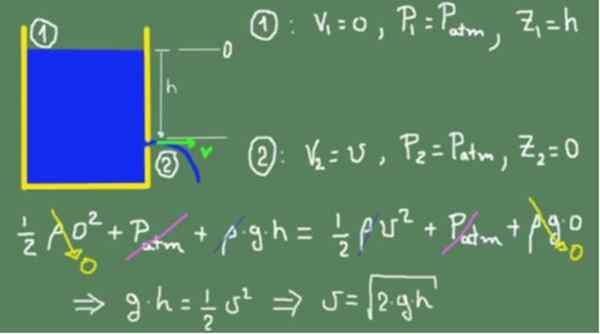

Edellinen laatikko osoittaa, että saatu tulos on sama kuin esineen, joka putoaa vapaasti,

Torricelli -periaate osoittaa.

Ratkaisut

Harjoitus 1

Yllyttää) Vesisäiliön pieni poistoputki on 3 m vedenpinnan alapuolella. Laske veden poistonopeus.

Ratkaisu:

Seuraava kuva osoittaa, kuinka Torricellin kaava sovelletaan tähän tapaukseen.

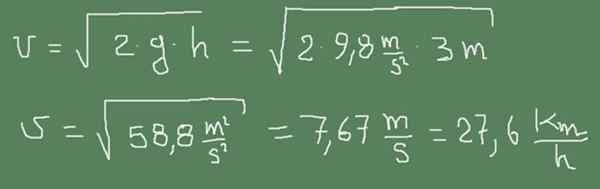
Harjoitus 2

II) Olettaen, että edellisen harjoitussäiliön lähtöputken halkaisija on 1 cm, laske veden poistovirtaus.

Ratkaisu:

Virtaus on nesteen tilavuus, joka tulee aikayksikköä kohti, ja se lasketaan yksinkertaisesti kertomalla lähtöreiän pinta -ala ulostulon nopeudella.

Seuraava kuva näyttää laskelman yksityiskohdat.

Harjoitus 3

III) Määritä, kuinka korkeus veden vapaa pinta on säiliössä, jos se tunnetaan

Se, että säiliön pohjassa olevassa reiässä vesi tulee 10 m/s.

Ratkaisu:

Jopa silloin, kun reikä on säiliön alaosassa, Torricellin kaava voidaan käyttää.

Seuraava kuva näyttää laskelman yksityiskohdat.

Viitteet

  1. Wikipedia. Torricelli -lause.
  2. Hewitt, s. Käsitteellinen fysiikka. Viides painos.119.
  3. Nuori, Hugh. 2016. Sears-Zanskyn yliopistofysiikka, jolla on moderni fysiikka. 14. ed. Pearson. 384.