Binomilause

Mikä on binominen lause?

Hän binomilause Se on yhtälö, joka kertoo meille, kuinka muodon ilmaisu kehittyy (A+B)ⁿ Joillekin luonnollisille numeroille n. Binomiaalinen ei ole muuta kuin kahden elementin summa, kuten (a+b). Se antaa meille myös tietää termille, jonka annetaan^{k -k -}b -^N-k Mikä on siihen liittyvä kerroin.

Tämä lause johtuu yleisesti englantilaisesta keksijältä, fyysisestä ja matemaatikosta Sir Isaac Newton; On kuitenkin havaittu erilaisia ​​tietueita, jotka osoittavat, että sen olemassaolo oli jo tiedossa Lähi -idässä, noin vuoden 1000.

Yhdistelmäluvut

Binom -lause kertoo matemaattisesti seuraavan:

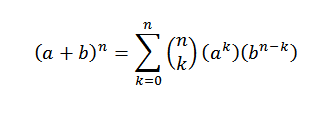
Tässä lausekkeessa A ja B ovat todellisia lukuja ja n on luonnollinen luku.

Ennen esittelyn esittämistä katsotaan joitain välttämättömiä peruskäsitteitä.

K: n yhdistelmä- tai yhdistelmät K: ssä ilmaistaan ​​seuraavasti:

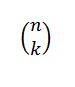
Tämä ilmaisee arvon, kuinka monta alajoukkoa K -elementeillä voidaan valita N -elementtien joukosta. Hänen algebrallisen ilmaisunsa on annettu:

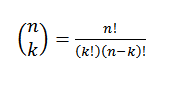
Katsotaanpa esimerkkiä: Oletetaan, että meillä on seitsemän pallon ryhmä, joista kaksi ovat punaisia ​​ja loput ovat sinisiä.

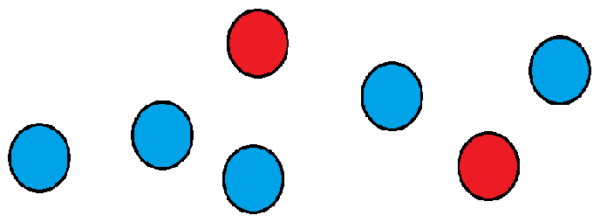
Haluamme tietää kuinka monella tapaa voimme tilata ne peräkkäin. Yksi tapa voisi olla sijoittaa kaksi punaista ensimmäiseen ja toiseen asentoon ja loput pallot jäljellä olevissa asennoissa.

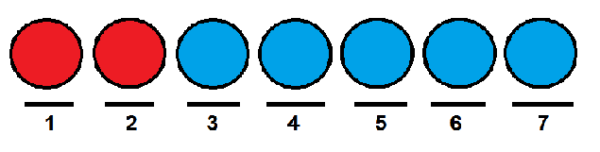
Samanlainen kuin edellisessä tapauksessa, voimme antaa punaiset pallot ensimmäisen ja viimeisen aseman ja miehittää muut sinisillä palloilla.

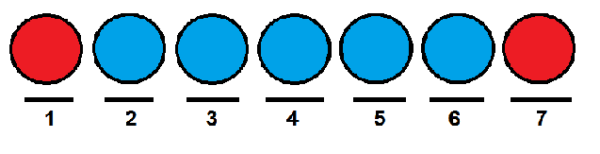
Nyt tehokas tapa laskea kuinka monta tapaa voimme tilata pallot peräkkäin, on yhdistelmälukujen käyttäminen. Voimme nähdä jokaisen sijainnin seuraavan sarjan elementtinä:

Voi palvella sinua: Täydelliset numerot: Kuinka tunnistaa ne ja esimerkkejä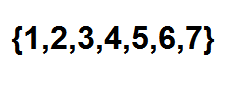

Alla on vain valita kaksi osaa, jossa kukin näistä elementeistä edustaa sijaintia, jonka punaiset pallot miehittävät. Voimme tehdä tämän valinnan:

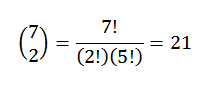
Tällä tavoin meillä on, että tällaisten pallojen tilaamiseen on 21 tapaa.

Tämän esimerkin yleinen idea on erittäin hyödyllinen binomin lauseen osoittamisessa. Katsotaanpa tiettyä tapausta: Jos n = 4, meillä on (A+B)⁴, Se ei ole muuta kuin:

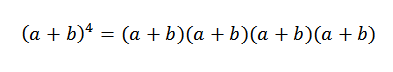
Kun kehitämme tätä tuotetta, meillä on termien summa, joka on saatu kertomalla kunkin neljän tekijän elementin (A+B). Siksi meillä on termejä, jotka ovat muodoltaan:

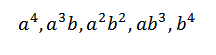
Jos halusimme saada lomakkeen termin⁴, Se riittää vain moninkertaistumaan seuraavasti:

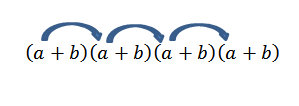
Huomaa, että tämä elementti on vain yksi tapa; Mutta mitä tapahtuu, jos etsimme nyt lomakkeen loppua²b -²? Koska "A" ja "B" ovat todellisia lukuja, ja siksi se on kommutatiivisen lain arvoinen, meidän on hankittava tämä termi on moninkertaistaa jäsenten kanssa, kuten nuolet osoittavat.

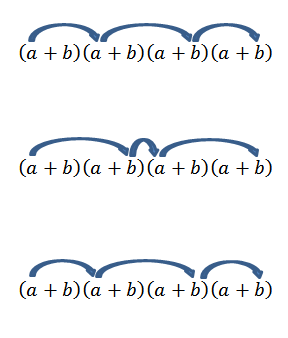
Kaikkien näiden operaatioiden suorittaminen on yleensä jonkin verran tylsää, mutta jos näemme termin "A" yhdistelmänä, jossa haluamme tietää, kuinka monella tapaa voimme valita kaksi "A": tä neljästä tekijästä, voimme käyttää ajatusta Edellinen esimerkki edellisestä esimerkistä. Joten meillä on seuraavat:

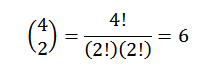
Siksi tiedämme, että lausekkeen lopullisessa kehityksessä (A+B)⁴ Meillä on tarkalleen 6²b -². Käyttämällä samaa ajatusta muihin elementteihin, sinun on:

Voi palvella sinua: Transcendent -numerot: Mitä ovat, kaavat, esimerkit, harjoitukset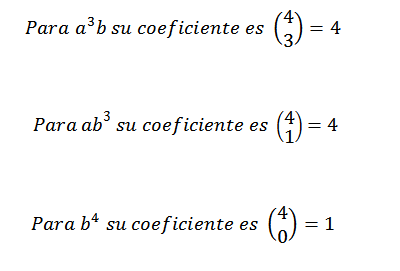

Sitten lisäämme yllä saadut lausekkeet ja meidän on:

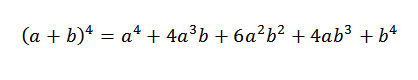
Se on muodollinen esittely yleiselle tapaukselle, jossa "n" on mikä tahansa luonnollinen luku.

Esittely

Huomaa, että kehitettäessä olevat termit (A+B)ⁿ Ne ovat muodoltaan^{k -k -}b -^N-k, missä k = 0,1,…, n. Edellisen esimerkin ideaa käyttämällä meillä on tapa valita "K" -muuttujat "A" "N" -tekijöistä on:

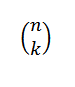
Kun valitsemme tällä tavalla, valitsemme automaattisesti N-K-muuttujat "B". Tämä seuraa sitä:

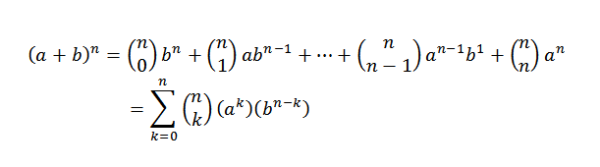
Esimerkit

Ottaen huomioon (A+B)⁵, Mikä olisi sinun kehityksesi?

Binomiaalisessa lauseessa meidän on:

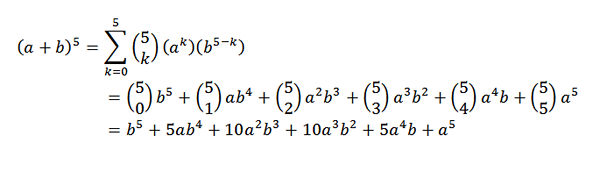
Binom -lause on erittäin hyödyllinen, jos meillä on lauseke, jossa haluamme tietää, mikä on tietyn termin kerroin joutumatta suorittamaan täydellistä kehitystä. Esimerkiksi voimme ottaa seuraavan tuntemattoman: mikä on X -kerroin⁷ja⁹ (X + y) kehityksessä¹⁶?

Binom -lauseessa meillä on, että kerroin on:

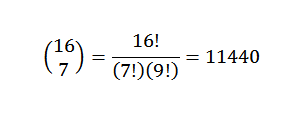
Toinen esimerkki olisi: mikä on x -kerroin⁵ja⁸ (3x-7y) kehityksessä¹³?

Ensin kirjoitamme ilmaisun uudelleen kätevällä tavalla; Tämä on:

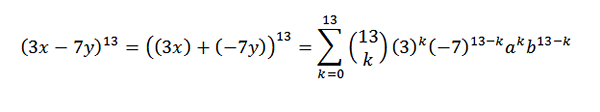
Sitten binomiaalista lausetta käyttämällä meillä on, että haluttu kertoimet on, kun sinulla on k = 5

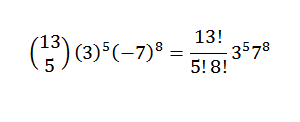
Toinen esimerkki tämän lauseen käytöstä on eräiden yleisten identiteettien, kuten alla mainitsemamme, osoittamisessa.

Identiteetti 1

Jos "N" on luonnollinen luku, meidän on:

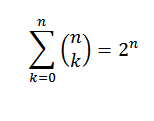
Esittelyä varten käytämme binomilausetta, jossa sekä "A" että "B" ottavat arvon 1. Sitten meillä on:

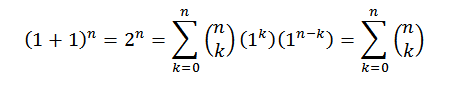
Tällä tavoin olemme todistaneet ensimmäisen identiteetin.

Voi palvella sinua: Satunnaiset valinnat korvaavan tai ilman

Identiteetti 2

Jos "n" on luonnollinen luku, niin niin

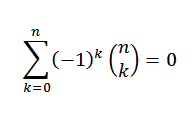
Binomiaalisessa lauseessa meidän on:

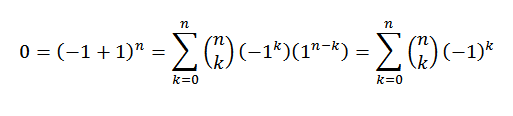
Toinen mielenosoitus

Voimme tehdä erilaisen mielenosoituksen binomilauseelle käyttämällä induktiivista menetelmää ja Pascalin identiteettiä, mikä kertoo meille, että jos "N" ja "K" ovat positiivisia kokonaislukuja, jotka täyttävät n ≥ k, sitten: sitten:

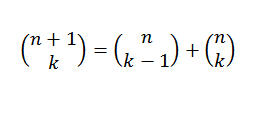
Induktion esittely

Katsotaanpa, että induktiivinen pohja on toteutunut.  Jos n = 1, meidän on:

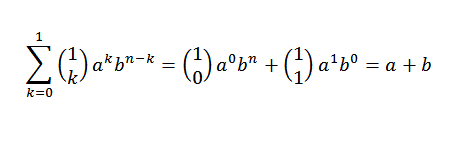
Itse asiassa näemme, että se täyttyy. Nyt joko n = J niin, että se täyttyy:

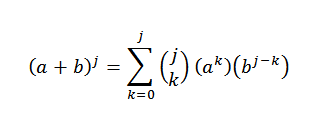
Haluamme nähdä, että n = j+1 on totta, että:

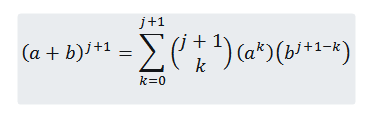
Joten meidän on:

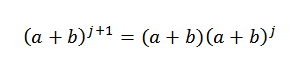
Hypoteesin avulla tiedämme sen:

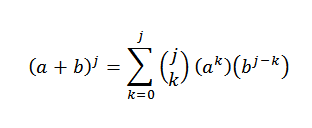
Sitten jakeluominaisuuden käyttäminen:

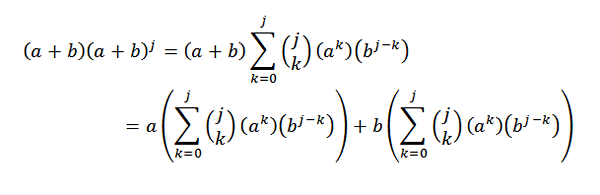
Myöhemmin jokaisen yhteenvedon kehittäminen on:

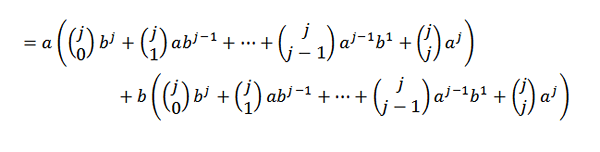
Nyt, jos ryhmittelemme kätevästi, meidän on:

Pascalin identiteetin avulla meidän on:

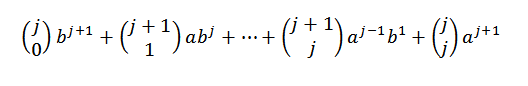
Huomaa lopuksi, että:

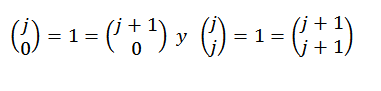
Siksi näemme, että binomilause täyttyy jokaiselle luonnolliselle numerolle kuuluvalle "N": lle, ja tämän avulla testi loppuu.

Uteliaisuus

Yhdistelmäluku (NK) kutsutaan myös binomikerroin, koska juuri binomin kehittymisessä esiintyvä kertoimet (A+B)ⁿ.

Isaac Newton antoi tämän lauseen yleistämisen tapaukseen, jossa eksponentti on todellinen luku; Tämä lause tunnetaan Newtonin binomalusemina.

Jo antiikin aikana tämä tulos oli tiedossa tietyssä tapauksessa, jossa n = 2. Tämä tapaus mainitaan Kohteet Euclid.