Selitystekijälause, esimerkit, harjoitukset

Hän tekijälause toteaa, että polynomi p (x) on jaettavissa muodon binomilla (x - a), jos x = a on p (x): n juuri, eli p (a) = 0. Sanotaan.

Polynomi on muodon ilmaisu:

P (x) = a_n xⁿ + -lla_N-1 x^N-1 +… + A₁ x + a_{0 -}

Kuvio 1. Tekijälause. Lähde: f. Zapata.

Missä:

-n on polynomin aste, ja se on suurin kokonaisluku, johon riippumaton muuttuja X nousee,

-Arvot a_n, -lla_N-1 ,… + A₁ , -lla_{0 -} Ne ovat polynomin kertoimia, jotka ovat yleensä todellisia lukuja, mutta ne voivat myös olla monimutkaisia ​​lukuja.

Luokan N polynomi voi hajota muodon binomien tuotteena:

(X - r_Yllyttää-A

Missä r_Yllyttää Se on i-alkish p (x) -juuri:

P (x) = a_n (X - r₁) (X - r₂)… (X - r_n-A

Koska polynomin juurten lukumäärä on yhtä suuri kuin saman aste.

[TOC]

Esimerkit

- Esimerkki 1

Harkitse polynomia tapauksen mukaan:

P (x) = 3⋅x² - 7⋅x + 2

Haluat tietää, onko tämä polynomi jaettava binomiaalilla (x - 2). Jos tekijälausetta käytetään, meidän on arvioitava p (x = 2) tietääksemme, onko arvo 2 juuri vai ei ole. Sitten jatkamme lausekkeen arviointia:

P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Osoittautuu, että x = 2 on p (x) -juuri, joten tekijälauseen mukaan binomiaalinen (x - 2) on todellakin tekijä p (x).

Siirrytään suoraan jaon tekemiseen. Yksityiskohta jaoston tekemisestä esitetään seuraavassa kuvassa:

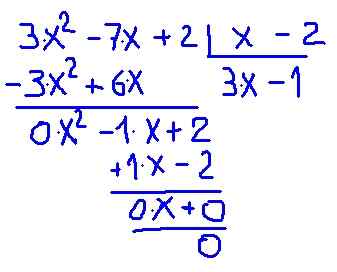Kuva 2.- Polynom jakautuminen P (x) binomiaalisen X-2: n välillä. Lähde: f. Zapata.

On varmistettu, että p (x): n ja (x -2): n välinen osoitus antaa vähäisen asteen polynomin, jota kutsutaan osamääräksi c (x) = 3⋅x - 1 jäännöksellä 0.

Voi palvella sinua: vektoritoiminnot

Voimme tiivistää tuloksen seuraavasti:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0

Aikaisempi lauseke voidaan kirjoittaa toisella tavalla, muistaa vain, että osinko p (x) on yhtä suuri kuin jakajan (x -2) tuote osamäärällä (3⋅x - 1) plus jäännös (nolla tässä tapauksessa tässä tapauksessa )

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

Tällä tavalla p (x) -polynomi (x), toisin sanoen kirjoittavat polynomien, alkuperäinen polynomi: alkuperäinen polynomi:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Esimerkki 2

Olla polynomi q (x) = x³ - x + 2. Haluat tietää, onko se jaettavissa binomiaalilla (x + 1).

Suorin tapa on yksinkertaisesti soveltaa tekijälause. Tässä tapauksessa sinun on vain varmistettava, onko x = -1 -vuotiaita vai ei polynomi q (x).

Jatkamme korvaamalla:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Tulos eroaa nollasta, joten tekijälause varmistaa, että polynomi q (x) ei ole jaettavissa (x + 1) välillä, koska q (-1) .

Nyt Q (x): n jako tehdään binomiaalin (x + 1) välillä johtopäätöksemme tarkistamismenetelmänä.

Tässä yhteydessä divisioona suoritetaan synteettisen jakautumismenetelmän avulla, joka koostuu sijoittamisesta ylimmän luokan ensimmäisen luokan rivillä kaikki polynomin kertoimet, myös puuttuvat, koska niillä ei ole kertoimia.

Sitten ensimmäisessä sarakkeessa jakajan riippumaton termi on sijoitettu, mutta merkki on muutettuna, jakaja on (x + 1). Sen riippumaton termi on 1, mutta kuten ensimmäisessä sarakkeessa se on asetettu muutettu merkki, eli -1.

Seuraava luku kuvaa, kuinka synteettinen jako suoritetaan:

Voi palvella sinua: polynomiyhtälöt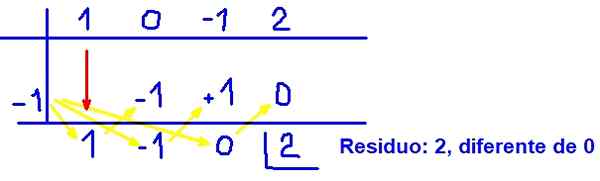Kuva 3. Esimerkki polynomisynteettisestä jakautumisesta. Lähde: f. Zapata.

Tällä tuloksella on todistettu, että (x + 1) se ei ole polynomin q (x) = x tekijä³ - x + 2, koska jäännös ei ole nolla.

Tämä johtopäätös ei ole yllättynyt, koska se oli jo ennustettu tekijälauseella. Huomaa, että kun korvataan x = -1 q (x), mikä saadaan, on juuri jäännös tai muu polynomin jako, koska q (-1) = jäännös = 2.

Tietysti divisioona tarjoaa lisätietoja osamäärästä c (x) = x² - x.

Muistamme, että osinko q (x) on yhtä suuri kuin jakaja (x + 1) suhteella c (x) plus jäännös r = 2, meillä on polynomin Q (x) laajennus seuraavasti:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

On huomattava, että tämä ekspressio ei ole mainitun polynomin tekijä, koska lisäys ei ole mitään, mikä on tarkalleen arvon arvo 2.

Harjoitukset

- Harjoitus 1

Löydä polynomit tekijät

P (x) = x³ - 5 x² + 2 x + 8

Ja kirjoita myös tekijä.

Ratkaisu

Tekijälause osoittaa, että meidän on etsittävä juuria -lla ja etsi sitten tekijät (x - -lla), Tässä tapauksessa, koska se on kolmen luokan polynomi, juuret on oltava kolme. 

Koska se on polynomi, jolla on kokonaiset kertoimet, juurten on oltava riippumattoman termin jakajien joukossa, joka tässä tapauksessa on 8. Nämä jakajat ovat:

± 1, ± 2, ± 4, ± 8.

Aloitamme tutkimalla +1: p (+1) = 1³ - 5⋅ 1² + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6, joka eroaa 0: sta, siksi +1 ei ole juuri.

Tutkimme -1:

P (-1) = (-1)³ - 5⋅ (-1)² + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Tuloksesta päätellään, että -1 on p (x) y (x -( -1)) = (x + 1) juuri on polynomikerroin.

Voi palvella sinua: vähimmäisruutuja

Meidän on löydettävä vielä kaksi tekijää:

Yritimme seuraavaa, joka on +2:

P (+2) = (+2)³ - 5⋅ (+2)² + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Jälleen saamme nollan. Sitten toinen tekijä on (x - 2).

Koska se on kolmas luokan polynomi, meidän on löydettävä vain tekijä. Nyt yritimme +4 -arvoa tietää, peruutetaanko polynomi:

P (+4) = (+4)³ - 5⋅ (+4)² + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Toisin sanoen.

Sinun ei tarvitse jatkaa etsimistä, koska se on luokan 3 polynomi, jolla on korkeintaan kolme juuria. Tässä harjoituksessa kaikki juuret osoittautuivat todellisiksi ja kokonaisiksi.

Siksi polynomi p (x) on tekijä näin:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Harjoitus 2

Olla P⋅x -polynomi³ - x + 2p. Määritä P: n arvo polynomille jaettattavana (x + 2).

Ratkaisu

Käytämme tekijälausetta, joka toteaa, että jos x = -2 peruuttaa polynomin, niin (x -( -2)) on mainitun polynomin tekijä.

Sitten x korvataan (-2) alkuperäisessä polynomissa, se yksinkertaistetaan ja vastaa nollaa:

P⋅ (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Nyt P: n arvo tyhjennetään siten, että tasa -arvo täyttyy nollaan:

P = -2 / 10 = -⅕ 

Tämä tarkoittaa sitä polynomia: 

-⅕⋅x³ - X - ⅖

Se on jaettavissa (x + 2) tai mikä vastaa: (x + 2) on yksi sen tekijöistä.

Viitteet

1. Baldor Aurelio. Algebra. Patria -toimitusryhmä.
2. Demana, w. Precáculculo: graafinen, numeerinen, algebrallinen 7. ed. Pearson -koulutus.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.