Toimintotyypit ja niiden kaaviot

On monipuolisia Toimintotyypit joita käytetään ongelmien mallintamiseen tiedonhaaroissa, kuten luonnontieteet, hallinto, talous ja yhteiskuntatieteet. Matemaattisesti ottaen funktio on suhde kahden tai useamman muuttujan välillä.

Monta kertaa tietyt esineet tai määrät liittyvät toisiinsa. Näitä määriä edustavat muuttujat. Esimerkiksi on olemassa kaksi liittyvää muuttujaa, jotka kuuluvat kahteen sarjaan A ja B, ei välttämättä numeerisia, vaikkakin suurimman osan ajasta ne ovat-.

Jotta voidaan pitää funktiona, tämän suhteen on täytettävä kaksi ehtoa: ensimmäinen on, että kaikki aloitusjoukon elementit osallistuvat, ja toinen, että jokainen mainitun joukon elementti liittyy vain yhteen sarjan B elementeihin.

Muuttujia kutsutaan yleensä kirjaimilla x ja ja, kanssa x kuin itsenäinen muuttuja ja ja kuin riippuva muuttuja. Luonnollisesti niitä voidaan kutsua millä tahansa muulla tavalla, valitsemalla muuttujan nimen sen edustaman suuruuden mukaisesti.

Näiden välinen suhde on merkitty kirjeen kautta F -tai toinen aakkosten kirjain, ja sitä esitetään monin tavoin, kuten joukko tilattuja pareja, kuvaaja, sanallinen lauseke tai algebrallinen kaava:

• f (x) = x + 1
• Tietyn kaupungin väestö P tietyllä aikavälillä T.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Toiminnot on ominaista verkkotunnus ja etäisyys tai reitti. Verkkotunnus on arvot, jotka muuttuja x Voit ottaa, kun alue on arvojoukko, joka saa riippuvan toiminnon tai muuttujan ja.

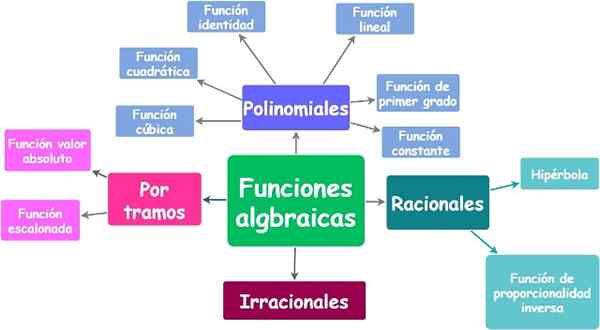
Toimintojen luokittelu

Toiminnot voidaan ryhmitellä viiteen suureen luokkaan, kuten seuraavassa järjestelmässä heijastuu, jossa kukin ryhmä on merkitty roomalaisella lukumäärällä ja värillä. Alkaen vasemmalta oikealle, toiminnot luokitellaan:

• I) sen muoto.
• Ii) symmetria.
• Iii) tapa ilmaista muuttuja.
• Iv) sen jatkuvuus ja monotonia.
• V) Tapa, jolla verkkotunnuselementit liittyvät alueen elementteihin.

Tärkeimmät luokittelukriteerit toiminnoille. Lähde: f. Zapata.

Seuraa nyt lyhyttä kuvausta jokaisesta funktiotyypistä vastaavilla esimerkeillä.

I) Toiminnot sen muodon mukaan

Yllyttää.1) Algebralliset toiminnot

Ne ovat useiden tieteen alan käytettyjä toimintoja, ja siksi ne ovat tunnetuimpia. Niille on ominaista, että sillä on kirjeenvaihtosääntö, algebrallinen lauseke.

Algebralliset funktiot puolestaan ​​on jaettu seuraaviin tyyppeihin:

• Yllyttää.1.a) polynomi tai polynomi.
• Yllyttää.1.b) rationaalinen.
• Yllyttää.1.c) irrationaalinen.
• Yllyttää.1.d) jaksoilla.

Algebralliset toiminnot ja niiden tyypit. Lähde: f. Zapata.

Yllyttää.1.a) polynomi- tai polynomifunktiot

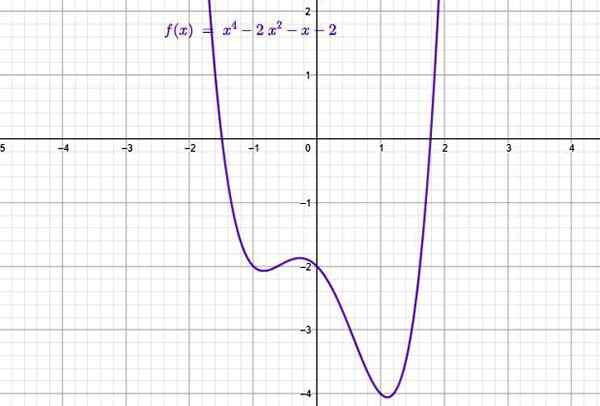Esimerkki polynomityyppisestä funktiosta. Lähde: f. Zapata Geogebran kautta.

Ne koostuvat termeistä, joiden yleinen muoto on:

P (x) = a_nxⁿ + -lla _N-1x^N-1 +…₁x + a_{0 -}

Missä kertoimet_n, -lla _N-1…₁, -lla_{0 -} Ne ovat todellisia lukuja ja n on kokonaisluku. Polynomifunktioiden alue on reaalilukujen R -R -alue ja ovat myös jatkuvia funktioita kyseisen alueen ajan.

Yläkuviossa on seuraava luokan 4 polynomifunktion kaavio:

f (x) = x⁴ - 2x² - x -2

Polynomifunktioiden joukossa jotkut tietyt tapaukset ovat erotettuja kertoimien arvojen mukaan. On syytä harkita huolellisesti, koska ne ovat erittäin hyödyllisiä useissa tilanteissa:

i) Jatkuva funktio

On jatkuvaa toimintoa, kun kaikki kertoimet peruutetaan, paitsi_{0 -}-

f (x) = a_{0 -} = k

Vakiofunktion kuvaaja on suora viiva, joka on yhdensuuntainen vaakasuoran akselin kanssa, kuten viivat:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

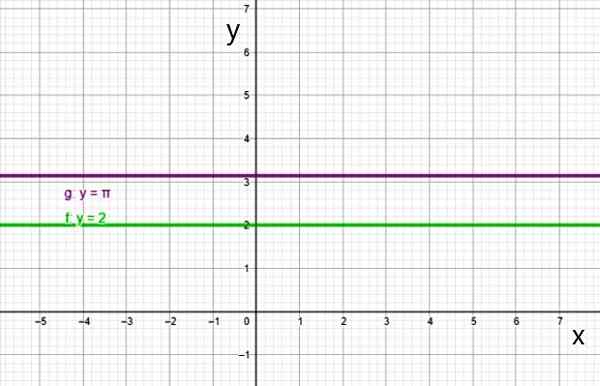Kaksi esimerkkiä jatkuvasta toiminnasta. Lähde: f. Zapata.

Ii) Ensimmäisen asteen funktio

Ensimmäinen -asteen funktio tai siihen liittyvä funktio on, että kenen kuvaaja on suora. Se on erityinen polynomifunktion tapaus, jossa kaikki mitäöin kertoimet₁ jo_{0 -}. Se on annettu:

f (x) = a₁x + a_{0 -}

Arvo a₁ Se on linjan kaltevuus, joka antaa sen kaltevuudestaan ​​ja_{0 -} Se on viivan leikkaus pystysuoran akselin kanssa. Molemmat voivat ottaa positiivisia tai negatiivisia arvoja.

Esimerkkejä ensimmäisen asteen toiminnasta ovat seuraavat:

• G (x) = 2x -1
• H (x) = -6x +5/2

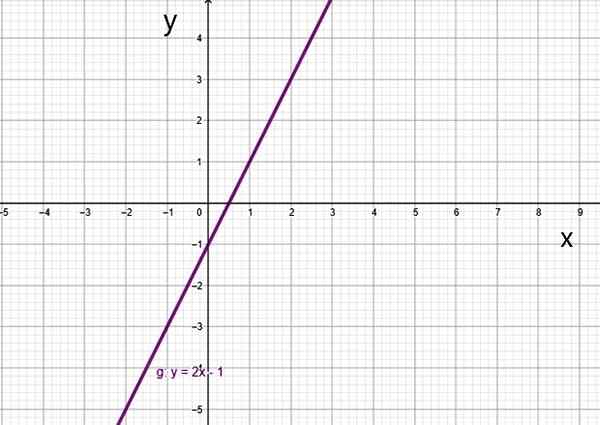Ensimmäisen asteen funktio F (x) = 2x-1. Lähde: f. Zapata.

On erityistapaus, joka on lineaarinen funktio.

Voi palvella sinua: Ryhmittelemättömän datan keskeiset taipumusmittaukset: Kaavat, harjoitukset

iii) lineaarinen funktio

Kun kertoimet_{0 -} Se on 0, funktio menee aina alkuperän läpi ja ilmaistaan ​​f (x) = a₁X, soittaminen lineaarinen toimenpide, mitä kuuluu:

• f (x) = 5x
• G (x) = -7x

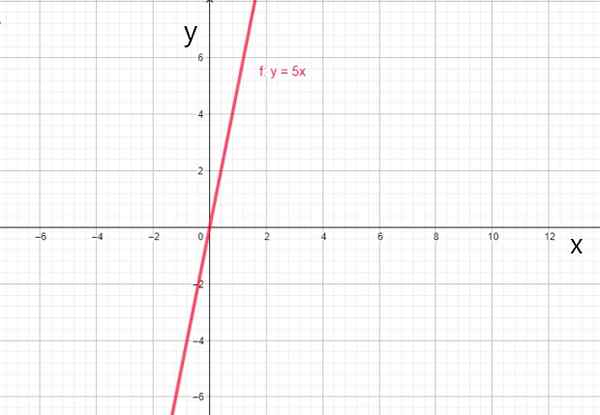Lineaarinen funktio f (x) = 5x. Lähde: f. Zapata.

iv) identiteettifunktio

Se on erityinen lineaarisen funktion tapaus, jossa₁ = 1:

f (x) = x

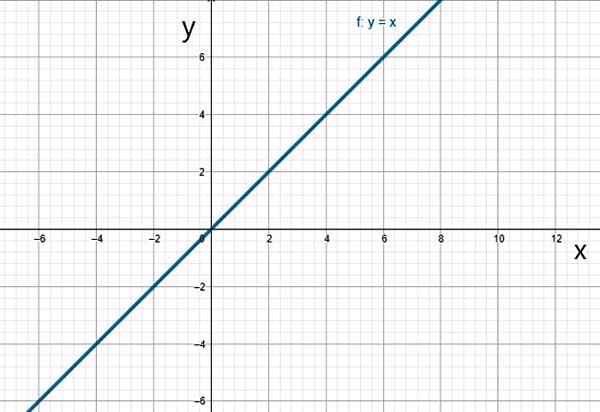Identiteettifunktio. Lähde: f. Zapata.

v) neliöfunktio

Sillä on yleinen muoto:

f (x) = a₂x² +-lla₁x + a_{0 -}

Kanssa₂  ≠ 0.

Sen kuvaaja on vertaus, jonka aksiaalinen tai symmetria -akseli on yhdensuuntainen ordinaattien akselin kanssa. Aina leikkaa pystysuoran akselin koordinaattipisteessä x = 0, y = a_{0 -}. Mitä tulee risteyksiin vaakasuoran akselin kanssa, sillä voi olla korkeintaan 2.

Esimerkkejä neliömäisistä toiminnoista ovat:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

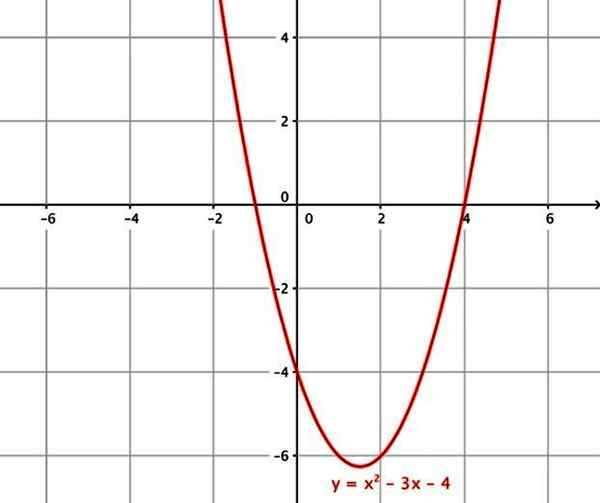Neliöfunktio. Lähde: Wikimedia Commons.

vi) kuutiomuoto

Kuten nimestä voi päätellä, kuutiofunktio sisältää 3: 3:

f (x) = a₃x³ + -lla₂x² + -lla₁x + a_{0 -}

Kerroin a₃ Se on aina erilainen kuin 0, kuten näissä tapauksissa:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

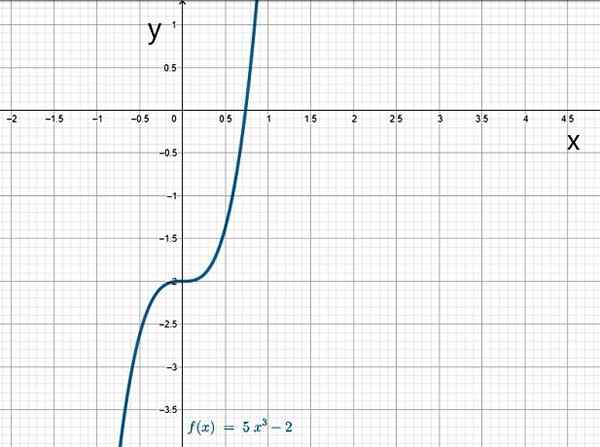Kuutiometri. Lähde: f. Zapata.

Yllyttää.1.b) rationaaliset toiminnot

Järkeillä toiminnoilla on muoto:

 Jos p (x) ja q (x) ovat peruuttamattomia polynomeja, ts. Niillä ei ole yleistä tekijää ja joka tapauksessa Q (x) ≠ 0.

Rationaalisten funktioiden alueelta kaikki arvot, jotka kuohuvat nimittäjän q (x), toisin sanoen sen juuret, kun taas arvojen arvot ja jotka määrittävät vaakasuuntaiset asymptotit.

Asymptootti on viiva, johon funktio lähestyy, sekä vasemmalla että oikealla, ylä- tai alapuolella, mutta ei koskaan ylittää. Tällaiset viivat voivat olla pystysuuntaisia, vaakasuoria tai kaltevia.

Esimerkkejä rationaalisista toiminnoista ovat:

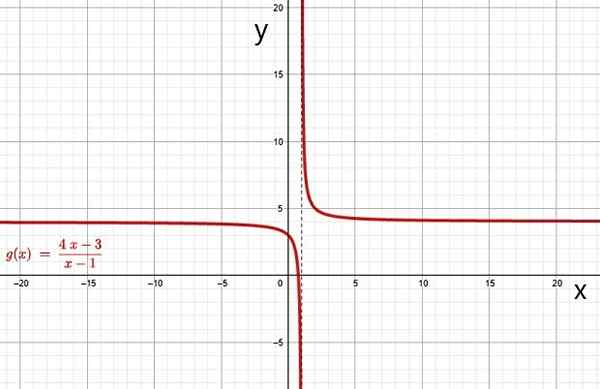Rationaalinen toiminta. Lähde: f. Zapata Geogebran kautta.

i) hyperbola

Rationaalisen funktion kuvaaja on hyperbola, kun nimittäjän p (x) -politilla on luokka 1. Yllä olevien esimerkkien funktioiden f (x) ja g (x) -kaavio ovat hyperbolas, se voidaan helposti tarkistaa ilmaisen online -grafiikkaohjelmiston, kuten geogebran, avulla.

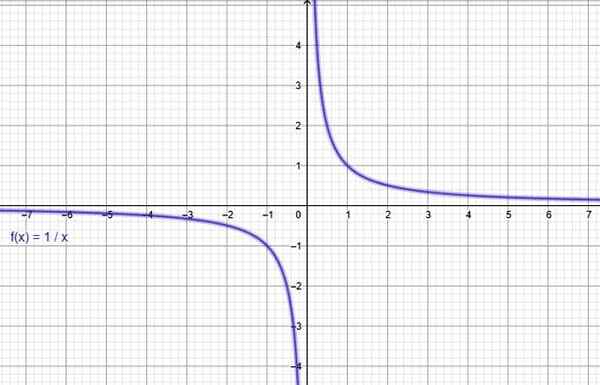Funktio y = 1/x. Lähde: f. Zapata Geogebran kautta.

Ii) Käänteinen suhteellisuusfunktio

Se on muodon funktio:

Missä c on todellinen numero, joka eroaa 0. Sen verkkotunnus on reaalilukujen joukko paitsi 0.

Yllyttää.1.c) Irrationaaliset toiminnot

Ovat niitä, joiden riippumaton muuttuja on radikaalin merkin alla. Sen yleinen muoto on:

Jotkut näistä toiminnoista voivat olla:

• 
• 

Näiden toimintojen alue määritetään seuraavasti:

-Jos juuret ovat vääntömomentin indeksiä, subradikaalin määrän F (x) on aina oltava 0 tai positiivinen.

-Kun juuret ovat outoja, f (x) voi olla positiivinen tai negatiivinen. Siksi tässä tapauksessa funktion alue on todelliset numerot.

Esimerkiksi: verkkotunnus:

Se on reaalilukujen joukko siten, että X-3 on suurempi tai yhtä suuri kuin 0. Tässä tapauksessa X: n on oltava suurempi tai yhtä suuri kuin 3. Siksi tämän funktion alue on aikavälin arvojoukko [3, ∞+).

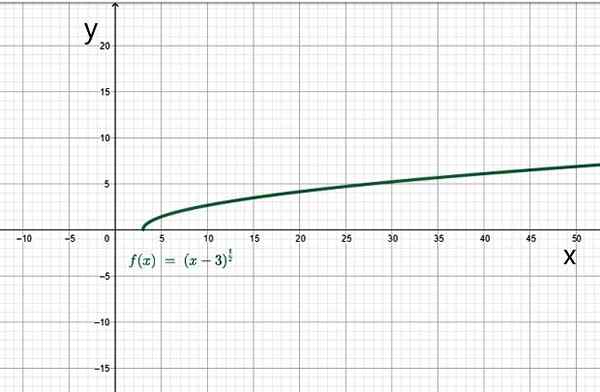 Esimerkki irrationaalisesta toiminnasta. Lähde: f. Zapata.

Yllyttää.1.d) Toiminnot kappaleiksi tai osiin

Osien funktio osioilla tai kappaleilla on yksi, joka vaatii useamman kuin yhden kaavan eri verkkotunnuksen arvoille. Tässä on joitain esimerkkejä sovelluksestasi:

-Pakettien lähettämisen hinnat postin mukaan.

-Palvelujen hinnat, esimerkiksi puhelin- ja sähkö.

-Lippujen myynti museoille tai huvipuistoille iästä riippuen.

Matemaattisessa muodossa funktio osittain voi olla esimerkiksi:

Funktion alue osissa riippuu sen määritelmästä. Edellisessä esimerkissä alue on sarja, jonka muodostuu: (-∞, -1) ∪ [1,+∞).

Absoluuttinen arvofunktio. Lähde: f. Zapata Geogebran kautta.

Ii) Escalonada -funktio

Tämän funktion kuvaaja osioilla koostuu vaiheista, kuten tikkaat tai voi olla eri korkeuksia, funktion määrittelemästä tavasta riippuen.

Se voi palvella sinua: Hipparco of Niza: Elämäkerta ja panos tieteeseen

Tätä varten valitaan rajallinen aika [a, b], joka sisältää tietyn äärellisen määrän epäjatkuvuuksia, nimeltään x_Yllyttää < x₁ < x₂ <… . x_n  Ja valitaan avoin aikaväli (x_Yllyttää , x_I+1) Antaa sille vakiona S_Yllyttää, Hyppyillä pisteissä x_Yllyttää. S: n arvo_Yllyttää Se on kyseisen vaiheen korkeus.

Esimerkki porrastetusta funktiosta on koko osa, joka vie minkä tahansa määrän ja yhdistää sen seuraavaan kokonaislukuun joko ylimääräisesti tai oletuksena. Seuraava on koko osa:

[x] = (suurempi kokonaisluku ≤ x)

Tämän toiminnon mukaan koko 2.5 on:

[2.5] = (suurempi kokonaisluku ≤ 2.5) = 2

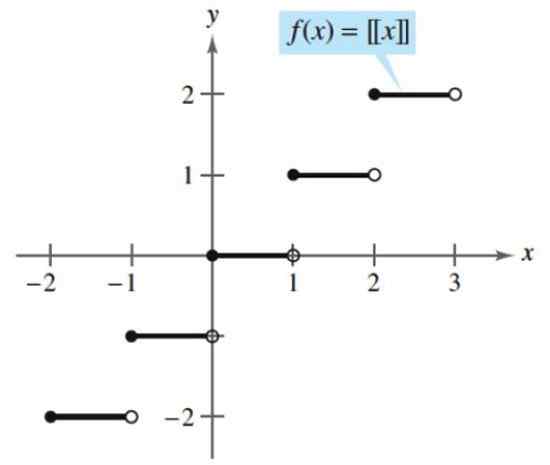Koko osa. Lähde: Larson, R. Laskenta analyyttisellä geometrialla. McGraw-Hill.

Yllyttää.2) Transcendent funktiot

Ei -algebrallisia funktioita kutsutaan transsendentteiksi. Eksponentiaaliset, logaritmiset ja trigonometriset funktiot ovat transsendenttisia funktioita.

Heissä muuttuja x Se on osa funktion argumenttia tai esimerkiksi jonkin juuren eksponentin tai indeksin osana:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

Transcendent -toiminnoilla on monia sovelluksia, esimerkiksi värähtelyjen ja aaltojen tutkimuksessa, todennäköisyysjakaumat, aaltojen mallintaminen, erilaisten populaatioiden kasvu, radioaktiivinen rappeutuminen, korot ja monet muut. 

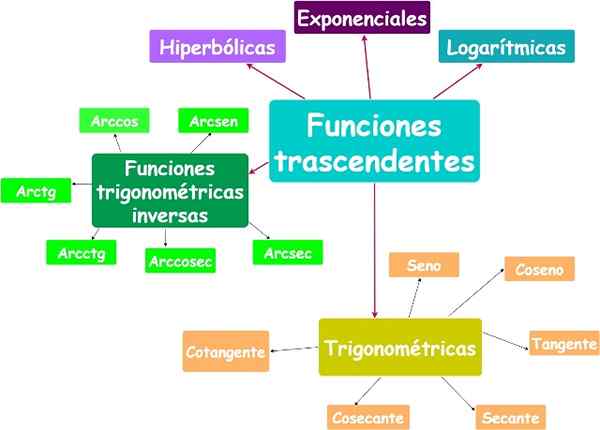Tärkeimmät transsendenttitoiminnot. Lähde: f. Zapata.

Yllyttää.2.a) Eksponentiaalinen funktio 

Eksponentiaalinen funktio on määritelty:

f (x) = a^x

Missä A on pohja, joka on aina positiivinen määrä 1 ja muuttuja, todellinen luku näkyy eksponentissa. Yleensä eksponentiaalinen funktio on kirjoitettu:

f (x) = a⋅a^Bx

Tässä a ja b ovat todellisia kertoimia. Seuraavat ovat tämän tyyppisiä funktioita:

• f (x) = 5e^x
• H (x) = 4. 10^5x
• g (t) = 8e^-2T

Pohja ja, missä ja Se on Euler 2: n lukumäärä.71828 ... esiintyy usein tieteen ja tekniikan ongelmissa sekä tilastoissa. Kun funktiolla on tätä pohjaa kutsutaan Luonnollinen eksponentiaalinen funktio.

Eksponentiaalisen funktion alue on reaalilukujen joukko, kun taas alue on positiiviset numerot.

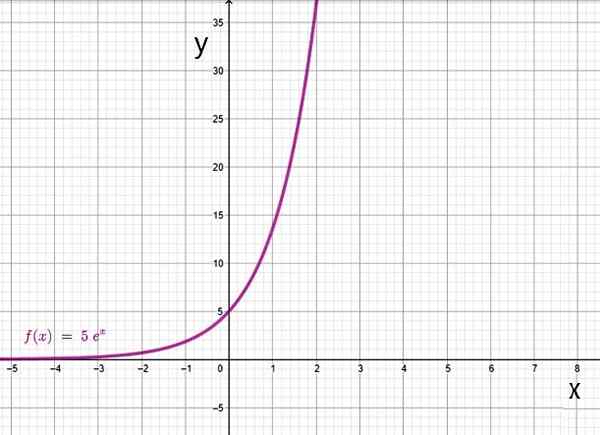Eksponentiaalinen funktio, joka perustuu. Lähde: f. Zapata Geogebran kautta.

Yllyttää.2.b) logaritmitoiminto

Puolestaan ​​logaritmitoiminto perustuu -lla Se on eksponentiaalisen funktion käänteinen funktio -lla. Joo:

Hirsi_-lla x = y

Niin:

x = a^ja

Erityisesti, jos logaritmin pohja on numero E, funktiota kutsutaan Neperian logaritmitoiminto Ja se on merkitty ln. Tämän tyyppiset toiminnot ovat:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

Logaritmifunktion alue, pohjasta riippumatta, ovat positiivisia todellisia lukuja, lukuun ottamatta 0. Eli negatiivisten lukujen logaritmeja tai 0 ei ole logaritmeja.

Logaritmi voi kuitenkin olla 0 tai negatiivinen: 0 ja 1: n lukumäärän logaritmi on negatiivinen ja sen puolestaan ​​saavutetaan_-lla 1 = 0.

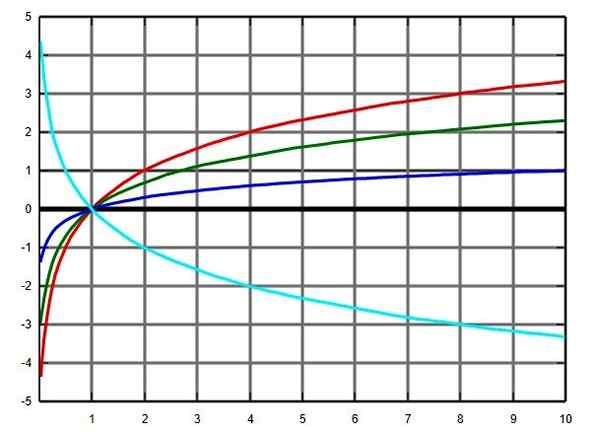Logaritmifunktiokaavio useissa emäksissä: pohja 2 punaisella, vihreällä e, sininen -pohja ja turkoosi pohjassa 0.5. Lähde: Wikimedia Commons.

Yllyttää.2.c) trigonometriset toiminnot

Ne ovat niitä, jotka tulevat trigonometrisistä syistä: sinus, kosiini, tangentti, kuivaus, harmoninen ja kulman x kerros. Ne on merkitty vastaavasti:

Sen X, COS X, TG X, Sec X, HAMM X ja COTG X

Ne ovat jaksollisia toimintoja, mikä tarkoittaa, että sen muoto on toistuva, joten ne ovat erittäin hyödyllisiä kuvaamaan luonnollisia ilmiöitä, kuten signaaleja, värähtelyjä, pyöreitä liikettä ja kääntöliikkeitä, joille on ominaista toistuva.

Esimerkkejä trigonometrisista toiminnoista ovat:

• f (x) = sin x
• G (t) = 5⋅cos (ωt + π)
• H (x) = tg (x/2)

Muuttuja X ilmaistaan ​​radianeissa.

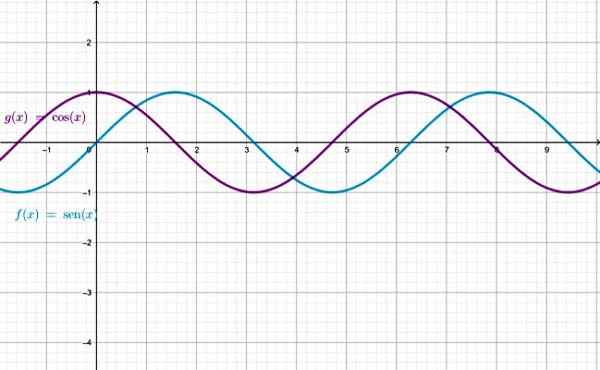Kaavio funktioista Sen x ja cos x, huomaa, että ne ovat identtisiä, paitsi että yksi on siirretty toiseen nähden. Lähde: f. Zapata Geogebran kautta.

Sen x- ja cos x -toimintojen hallitseminen on reaalilukujen joukko. Jäljellä oleville funktioille on X -arvoja, joille funktiota ei ole määritelty:

-TG X -toimintoa ei ole, kun x = ± π /2, ± 5π /2 ... tämä on, kaikki parittomat kertoimet π /2.

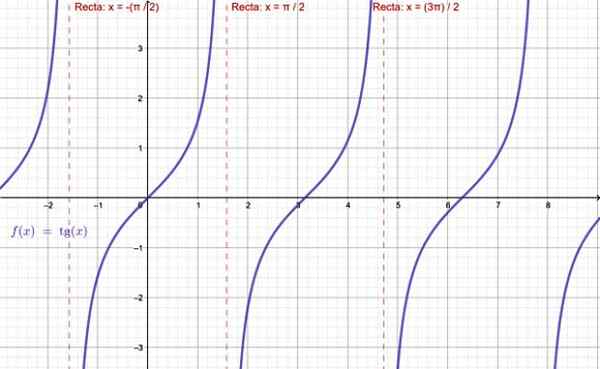Tangenttifunktion kuvaus. Lähde: f. Zapata Geogebran kautta.

-Mitä f (x) = coTg x, tätä toimintoa ei ole määritelty koko π: ± π, ± 2π, ± 3π ..

Voi palvella sinua: Merkkien laki

-Y = SEC X -funktio ei ole kelvollinen, kun cos x = 0, joka sulkee pois x = ± π /2, ± 5π /2… sen alueesta.

-Lopuksi, f (x) = haittaa x, koko π -kertoimet eivät kuulu niiden alueeseen.

Yllyttää.2.d) hyperboliset toiminnot

Hyperboliset funktiot ovat erityisiä eksponentiaalisia yhdistelmiä ja^x ja e^-x Ja niitä kutsutaan rintaan, Coseno .. .hyperbolinen. Kuten trigonometriset funktiot, joita kutsutaan myös "ympyräksi", on 6 hyperbolista funktiota:

-Hyperbolinen sinus Senh X:

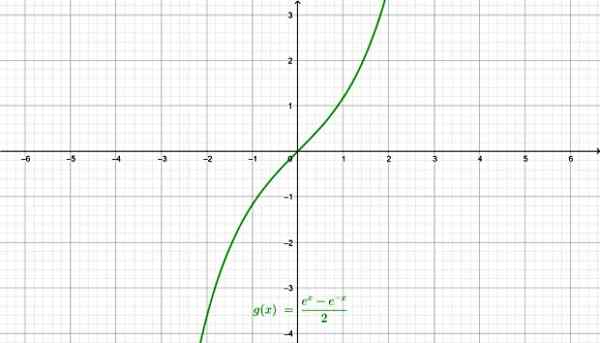Hyperbolinen sinusfunktio. Lähde: f. Zapata Geogebran kautta.

-Hyperbolinen kosiini Cosh X:

 -Hyperbolinen tangentti Tanh X:

 -Hyperbolinen harvesteri CSCH X:

 -Hyperbolinen Secant SECH X:

-Hyperbolinen kotangentti Coth x:

Joustava kaapeli, joka on valmistettu yhtenäisestä ja roikkuvasta materiaalista kahden pisteen välillä, on nimeltään käyrän muotoinen kissanarviointi, joka ilmaistaan ​​hyperbolisena kosinina:

Yllyttää.2.e) Käänteiset trigonometriset toiminnot

Ne vastaavat trigonometristen funktioiden käänteistä. Esimerkiksi mikä olisi kulma (kaari), jonka rinta on 0.5?

Vastaus on ARC SEN 0.5, joka lukee ”kaari sinus 0.5 ”, ja tämä kulma on 30º, vaikka periaatteessa tämä ei olisi ainoa kulma, jonka rinta on 0.5, koska Sen X -toiminto on määräajoin. Mitä tapahtuu, jos sen X -funktio otetaan koko alueensa ajan, sillä ei olisi käänteistä, joten Arcoseno -toimintoa ei voitu määritellä. Aihe ratkaisee rajoittamalla kaikki kulmiin välillä -π/2 ja +π/2.

Tämä voidaan ilmaista seuraavasti:

Jos kaari sen x = θ, se tarkoittaa, että sin θ = x

-Π/2 ≤ θ ≤ π/2: lla.

Toinen ARC SEN X: lle käytetty merkintä on f (x) = synti^-1 x. Kaavio on esitetty alla:

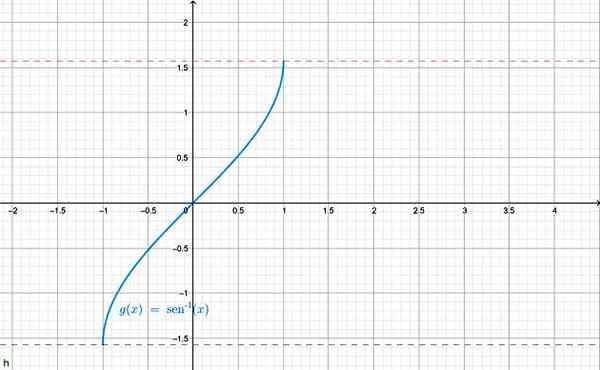Arcsen X -toimintografiikka. Lähde: f. Zapata Geogebran kautta.

On myös mahdollista määritellä käänteinen muille trigonometrisille funktioille, esimerkiksi: Arc cos x = θ ja siten. Jokaiselle sijoitusta on rajoitettu oikein, vastaavan trigonometrisen funktion käänteiseksi.

Ii) Toiminnot sen symmetrian mukaan

II.1) par

Jos kaikille f (x) -alueelle kuuluville X: lle on toteutettu, että:

f (x) = f (-x)

Sanotaan, että funktio on tasainen, kuten seuraavat:

• f (x) = x² - 3
• g (x) = cos x
• 

  Esimerkki paritoiminnosta. Lähde: f. Zapata Geogebran kautta.

Esimerkiksi x = 1 sisään f (x) = x² - 3 on saatu:

f (1) = 1² - 3 = -2.

Ja jos x = -1, niin:

f (-1) = (-1)² - 3 = -2.

Molemmat tulokset ovat identtisiä.

Edellisillä toiminnoilla on symmetria pystysuoran akselin ympärillä, kuten edellisessä kuvassa voidaan nähdä.

II.2) pariton funktio

Toisaalta kyllä:

f (-x) = -f (x)

Toiminto on outo.

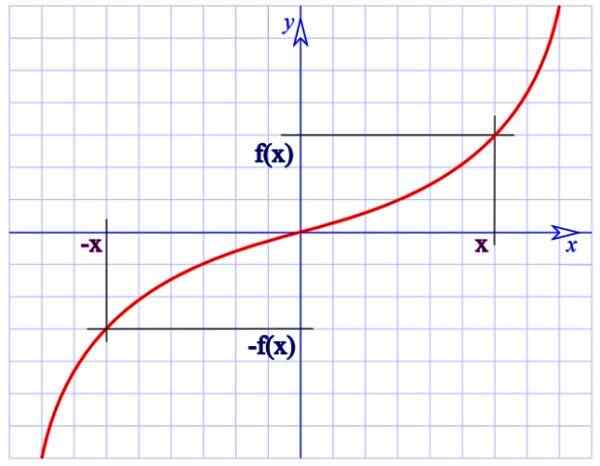Pariton funktio. Lähde: Wikimedia Commons.

Esimerkiksi ylemmän kuvan funktio f (x) = 1/x on pariton, koska:

f (-x) = -1/x

JA

-f (x) = -1/x

Toinen tärkeä impar -funktio on f (x) = sin x.

Huomaa, että parittomilla funktioilla on 180º: n kiertosymmetria alkuperän ympärillä (kuvaajaa ei muuteta, jos jokainen sen piste käännetään 180º koordinaattien alkuperän suhteen).

Iii) Toiminta muuttujan ekspression mukaan

III.1) Selkeät toiminnot

Ne ilmaistaan ​​suoraan riippuvaisen muuttujan, kuten y = f (x): n suhteen. Esimerkiksi:

• f (x) = x³

III.2) implisiittiset toiminnot

Implisiittisissä funktioissa mikään muuttujista ei näytä selvältä. Ne ilmaistaan ​​nimellä f (x, y) = 0, kuten:

• x² + ja² -3xy = 0
• xy = - x²+ X-5

Tässä artikkelissa kuvatut toiminnot ovat nimenomaisia ​​funktioita.

Iv) Toiminnot grafiikan mukaan

Kaavionsa mukaan funktiot voivat olla jatkuvia tai epäjatkuvia. Jatkuvat toiminnot voidaan jäljittää keskeyttämättä aivohalvausta, toisaalta epäjatkuvasti toiminnot ovat hyppyjä. Seuraavassa kuvassa funktio on epäjatkuva x = a:

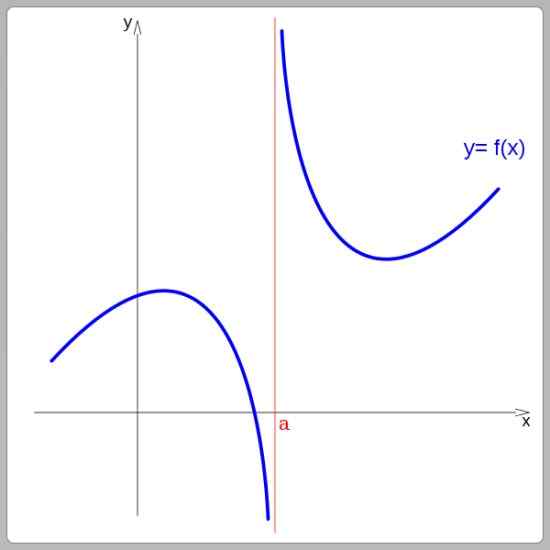Epäjatkuvuusfunktio x = a. Lähde: Wikimedia Commons.

Esimerkkejä jatkuvista toiminnoista ovat lineaarinen funktio, neliöfunktio sekä sini- ja kosinifunktiot. Ja epäjatkuvien funktioiden joukossa ovat porrastettu funktio ja tangenttitoiminto.

V) Toiminnut verkkotunnuksen elementtien ja alueen välisen suhteen mukaan

V.1) injektiotoiminto

Toiminto on Injektiivinen Kun lähtö- tai verkkotunnusjoukossa ei ole kahta eri elementtiä, joilla on sama kuva saapumisjoukossa.

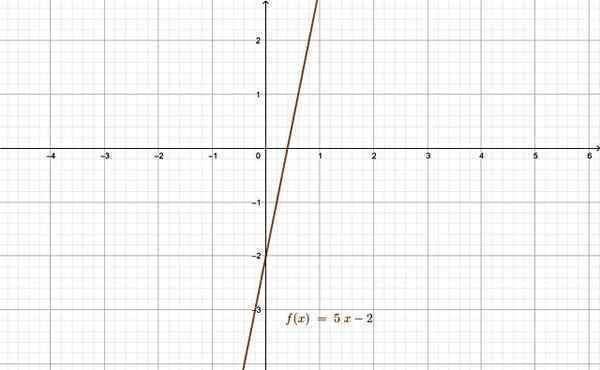
Oletetaan, että todelliset toiminnot ovat, ellei esimerkiksi toisin mainita:

f (x) = 5x -2

Kaikilla F (x) -alueelle kuuluvalle X -arvolle, joka on todellisten lukujen sarja ℛ, on ainutlaatuinen, myös todellinen kuva. Toisaalta tässä toisessa toiminnossa:

g (x) = x²

Verkkotunnuksella on erilaisia ​​elementtejä, joilla on sama kuva, esimerkiksi x₁= 2 ja x₂= -2:

G (2) = g (-2) = 4.

Tapa tunnistaa injektiivinen funktio sen kuvaajasta on kaatavan viivan piirtäminen, jos se leikataan käyrään useammassa kuin yhdessä pisteessä, funktio ei ole injektiivinen.

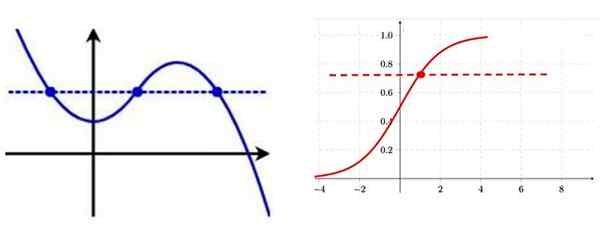Vasemmalla olevalla injektiofunktiolla on, että kaaviossa on useita pisteitä samalla pystysuuntaisella koordinaatilla. Oikealla injektiofunktiolla, jokaisessa käyrän kohdassa on tietty "Y" -koordinaatti. Lähde: f. Zapata.

V.2) Overjektiivitoiminto

Siinä onjektiivitoiminnot, Kaikki saapumisjoukon elementit ovat kuva jonkin lähtösarjan elementtiä. Esimerkki liiajektiivisesta funktiosta on sama f (x) = 5x -2, mutta g (x) = x² Ei ole, koska otetut arvot (x) ovat vain positiivisia todellisia ja 0.

Verkkotunnus voitaisiin kuitenkin määritellä uudelleen siten, että g (x) oli liiallinen, jos esimerkiksi se muuttuu kaikkiin positiivisiin todellisiin plus 0. 

V.3) Bijektiivifunktio

Lopuksi kutsutaan toimintoa, joka on sekä injektio- että liiallinen Bijektiivi. Esimerkkejä bijektiivifunktioista ovat: liittyvä funktio, eksponentiaalinen funktio ja logaritmitoiminto.

Aiheeseen liittyvä funktio on hyvä esimerkki bjjektiivitoiminnosta. Lähde: f. Zapata Geogebran kautta.

Viitteet

1. E-math-vyöhyke. Toimintotyypit. Toipunut: Emathzone.com.
2. Hoffman, J.G. Matematiikan aiheiden valinta. Ed. Spphinx.
3. Matematiikka on hauskaa. Commons Function -viite. Toipunut: Mathisfun.com.
4. Requena, b. Maailmankaikkeuden kaavat. Toimintotyypit. Toipunut: UniversOformulat.com.
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.