Paraboliset laukauksen ominaisuudet, kaavat ja yhtälöt, esimerkit

Hän parabolinen laukaus Se koostuu esineen tai ammuksen heittämisestä tietyllä kulmalla ja antamalla sen liikkua painovoiman alla. Jos ilmankestävyyttä ei oteta huomioon, esine, sen luonteesta riippumatta.

Se on päivittäinen liike, koska suosituimpien urheilulajien joukossa on niitä.

Kuvio 1. Koristeen lähteen vesisuihku seuraa parabolista etenemissuuntausta. Lähde: Wikimedia Commons. Zátonyi Sandor (IFJ.), Fizped/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)

Tutkimusta varten parabolinen laukaus jaotellaan kahteen päällekkäiseen liikkeeseen: yksi vaakasuora ilman kiihtyvyyttä ja toinen pystysuora jatkuvan kiihtyvyyden ollessa alaspäin, joka on painovoima. Molemmilla liikkeillä on ensimmäinen nopeus.

Oletetaan, että vaakasuuntainen liike kestää. Jokainen näistä liikkeistä on riippumaton toisesta.

Ottaen huomioon, että ammuksen sijainnin määrittäminen on päätavoitteita, on tarpeen valita sopiva referenssijärjestelmä. Yksityiskohdat tulevat seuraavaksi.

[TOC]

Parabolisen laukauksen kaavat ja yhtälöt

Oletetaan, että esine heitetään kulmalla α vaakasuoraan ja alkuperäiseen nopeuteen v_jompikumpi Kuten alla olevassa kuvassa on esitetty. Parabolinen laukaus on lentokoneessa tapahtuva liike Xy Ja siinä tapauksessa alkuperäinen nopeus hajoaa näin:

v_härkä = v_jompikumpi cos α

v_Oy = v_jompikumpi synti α

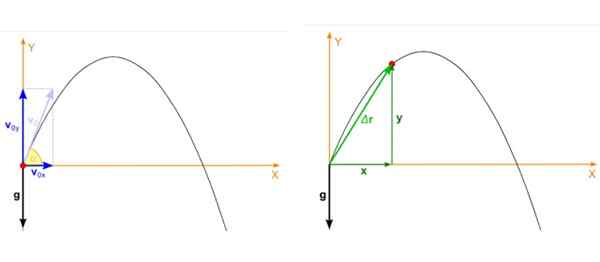Kuva 2. Vasemmalla puolella ammuksen alkuperäinen nopeus ja oikealle sijainti milloin tahansa käynnistyshetkellä. Lähde: Wikimedia Commons. Zátonyi Sandor (IFJ.) Fizped/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0).

Ammus -sijainti, joka on kuvan 2 punainen piste, oikeassa kuvassa, on myös kaksi komponenttia, jotka riippuvat ajasta, yksi sisään x Ja toinen sisään ja. Sijainti on vektori, joka on merkitty r - ja sen yksiköt ovat pituisia.

Voi palvella sinua: isomeria

Kuvassa ammuksen alkuperäinen sijainti tapahtuu koordinaattijärjestelmän alkuperän kanssa, joten x_jompikumpi = 0, ja_jompikumpi = 0. Tämä ei aina ole tilanne, alkuperä voidaan valita missä tahansa, mutta tämä valinta yksinkertaistaa laskelmia paljon.

Mitä tulee kahteen liikkeeseen x: ssä ja y: ssä, nämä ovat:

-X (t): se on tasainen suorakulmainen liike.

-ja (t): vastaa tasaisesti kiihdytettyä suorakulmaista liikettä g = 9: llä.8 m/s² ja osoittaen pystysuunnassa.

Matemaattisessa muodossa:

x (t) = v_jompikumpi cos α.t

ja (t) = v_jompikumpi .synti α.T - ½ g.t²

Sijaintivektori pysyy:

r - (t) = [v_jompikumpi cos α.t]Yllyttää + [V_jompikumpi .synti α.T - ½ g.t²- J -

Näissä yhtälöissä tarkkaavainen lukija huomaa, että miinusmerkki johtuu siitä, että vakavuus osoittaa maahan, aisti, joka valitaan negatiiviseksi, kun taas ylöspäin sitä pidetään positiivisena.

Koska nopeus on ensimmäinen asemasta johdettu, se riittää saamaan r - (t) Ajan suhteen ja hanki:

v (t) = v_jompikumpi cos α Yllyttää + (V_jompikumpi .synti α - Gt) J -

Lopuksi kiihtyvyys ilmaistaan ​​vektorisesti kuten:

-lla (t) = -g J -

- Etenemissuunta, maksimikorkeus, maksimaalinen aika ja vaakasuora ulottuvuus

Suunta

Löydät radan nimenomaisen yhtälön, joka on käyrä y (x), sinun on poistettava aikaparametri, tyhjentäminen x (t) -yhtälössä ja korvattava y (t) -sarjassa. Yksinkertaistaminen on jonkin verran työlästä, mutta lopulta se saadaan:

Enimmäiskorkeus

Suurin korkeus tapahtuu kun v_ja = 0. Tietäen, että aseman ja nopeuden neliön välillä on seuraava suhde:

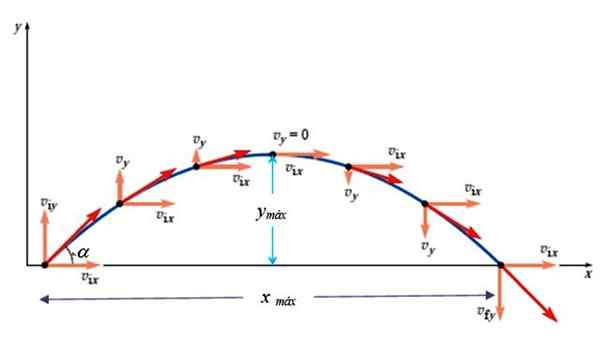Kuva 3. Parabolisen laukauksen nopeus. Lähde: Giambattista, a. Fysiikka.

v_ja² = v_Oy ²- 2Gy

Tekeminen v_ja = 0 Juuri kun se saavuttaa enimmäiskorkeuden:

0 = V_Oy ²- 2 g.ja_max → ja_max = v_Oy ²/2 g

Kanssa:

Voi palvella sinua: Centripetal kiihtyvyys: Määritelmä, kaavat, laskenta, harjoitukset

v_Oy = v_jompikumpi seti

Enimmäisaika

Suurin aika on aika, jonka esine kulkee saavuttamiseen ja_max. Sen laskemiseksi sitä käytetään:

v_ja = v_jompikumpi .synti α - GT

Sen tietäen v_ja Se on tehty 0 milloin t = t_max, tulos:

v_jompikumpi .synti α - g.t_max = 0

t_max = v_Oy /g

Suurin vaakasuuntainen alue ja lentoaika

Soveltamisala on erittäin tärkeä, koska se osoittaa, mihin esine putoaa. Joten tiedämme, antaako se valkoista vai ei. Sen löytämiseksi tarvitsemme lentoaikaa, kokonaisaika tai t_v.

Aikaisemmasta kuvasta on helppo päätellä t_v = 2.t_max. Mutta huomio on totta vain, jos lanseeraus on tasolla, ts. Lähtöpisteen korkeus on sama kuin saapumisen korkeus. Muuten aika on toisen asteen yhtälön ratkaiseminen, joka johtuu lopullisen sijainnin korvaamisesta ja_lopullinen-

ja_lopullinen = v_jompikumpi .synti α.t_v - ½ g.t_v²

Joka tapauksessa vaaka -asteikko on:

x_max = v_härkä. t_v

Parabolinen ammunta -esimerkit

Parabolinen laukaus on osa ihmisten ja eläinten liikettä. Myös melkein kaikista urheilulajeista ja peleistä, joissa painovoima puuttuu. Esimerkiksi:

Parabolinen ammunta ihmisen toiminnassa

-Katapultti heitetty kivi.

-Maalivahti maalivahdin potku.

-Pallo, joka heittää syöttäjän.

-Arkista tulee nuoli.

-Kaikenlaisia ​​hyppyjä

-Heittää kivi.

-Kaikki heittäjäase.

Kuva 4. Katapultin ja patey pallo viimeistelylaatikkoon ovat esimerkkejä parabolisista laukauksista. Lähde: Wikimedia Commons.

Parabolinen laukaus luonnossa

-Vesi itävät luonnollisista tai keinotekoisista suihkukoneista, kuten lähteen.

-Kivet ja laava itävät tulivuoresta.

-Pallo, joka pomppii jalkakäytävällä tai kivillä, joka tekee sen vedessä.

-Kaikenlaisia ​​eläimiä, jotka hyppäävät: kenguru, delfiinit, gazellit, kissat, sammakot, kanit tai hyönteiset, mainitta.

Se voi palvella sinua: Mekaaninen voima: Mikä on, sovellukset, esimerkitKuva 5. Impala pystyy hyppäämään jopa 3 m. Lähde: Wikimedia Commons. Arturo de Frias Marques/CC BY-S (https: // creativecommons.Org/lisenssit/by-SA/3.0).

Harjoittele

Heinäsirkka, joka muodostaa 55 º: n kulman vaakasuoraan ja laskeutuu 0: lla.80 metriä myöhemmin. Löytö:

a) saavutettu enimmäiskorkeus.

b) Jos hyppään samalla alkuperäisellä nopeudella, mutta muodostaen 45º kulman, saisiko se korkeammalle?

c) Mitä voidaan sanoa tämän kulman maksimaalisesta vaakasuunnasta?

Liittää jhk

Kun ongelman tarjoamat tiedot eivät sisällä alkuperäistä nopeutta V_jompikumpi Laskelmat ovat jonkin verran työläisempiä, mutta tunnetuista yhtälöistä voidaan päätellä uusi lauseke. Alkaen:

x_max = v_härkä . t_lento = v_jompikumpi.cos α. t_v

Kun se laskeutuu myöhemmin, korkeus on jälleen 0, sitten:

v_jompikumpi .synti α.t_v - ½ g.t_v²= 0

Kuten t_v Se on yleinen tekijä, sitä yksinkertaistetaan:

v_jompikumpi .synti α - ½ g.t_v= 0

Voimme tyhjentää t_v Ensimmäisestä yhtälöstä:

t_v = x_max / v_jompikumpi.cos α

Ja korvaa toisessa:

v_jompikumpi .synti α - (½ g.x_max / v_jompikumpi.cos α) = 0

Kertomalla kaikki termit v_jompikumpi.cos αIlmaisu ei muuta ja nimittäjä katoaa:

(V_jompikumpi .synti α.-A (V_jompikumpi.cos α) - ½ g.x_max = 0

v_jompikumpi² synti α. cos α = ½ g.x_max

Voidaan jo puhdistaa V_jompikumpi tai korvaa myös seuraava henkilöllisyys:

SEN 2a = 2 SEN α. cos α → V_jompikumpi² SEN 2a = g.x_max

On laskettu v_jompikumpi²-

v_jompikumpi² = g.x_max - SEN 2a = (9.8 x 0.8 / Sen 110) m²/s² = 8.34 m²/s²

Ja lopuksi enimmäiskorkeus:

ja_max= v_Oy ²/2G = (8.34 X SEN² 55)/(2 x 9.8) M = 0.286 M = 28.6 cm

Ratkaisu b

Hummeri onnistuu ylläpitämään saman vaakasuoran nopeuden, mutta kun kulma vähenee:

ja_max= v_Oy ²/2G = (8.34 X SEN² 45)/(2 x 9.8) M = 0.213 m = 21.3 cm

Saavuttaa pienemmän korkeuden.

Liuos C

Suurin vaakasuuntainen laajuus on:

x_max = v_jompikumpi² Sen 2A / g

Kun kulma vaihtelee, vaakasuuntainen laajuus muuttuu myös:

x_max = 8.3. 4 Sen 90 / 9.8  M = 0.851 m = 85.1 cm

Hyppy on nyt pidempi. Lukija voi varmistaa, että se on maksimikulma 45 º: lle sitten:

sin 2a = sin 90 = 1.

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysiikka. Toinen painos. McGraw Hill.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Resnick, r. 1999. Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.