Laplace -muunnos

Mikä on Laplacen muutos?

Se Laplace -muunnos Se on ollut viime vuosina erittäin tärkeitä tekniikassa, matematiikassa, fysiikassa muun muassa, koska teoreettisen kiinnostamisen lisäksi se tarjoaa yksinkertaisen tavan ratkaista differentiaaliyhtälöt, muuttamalla ne algebraksi yhtälöiksi.

Alun perin Laplace-muunnon esitteli Pierre-Simon Laplace (1745-1827) todennäköisyyden teoriaa koskevassa tutkimuksessaan, ja periaatteessa sitä käsiteltiin pelkästään teoreettisen edun matemaattisena kohteena.

Nykyiset sovellukset syntyvät, kun erilaiset matemaatikot yrittivät antaa muodollisen perusteen Oliver Heaviside (1850-1925) käyttämille ”operatiivisille säännöille” sähkömagneettisen teorian yhtälöiden tutkimuksessa.

Määritelmä Laplace -muunnos

Olkoon f määritelty funktio t ≥ 0. Laplace -muunnos määritellään seuraavasti:

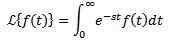
Sanotaan.

Yleensä merkitsee funktiota, jota halutaan muuttaa pieniä kirjaimia, ja pääomakirje vastaa sen muutosta. Tällä tavalla meillä on:

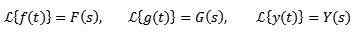
Esimerkit

Harkitse vakiotoimintoa f (t) = 1. Meidän on muutettava:

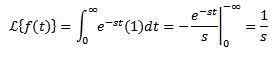
Edellyttäen, että integraali lähenee, ts. Edellyttäen, että S> 0. Muuten s < 0, la integral diverge.

Olkoon g (t) = t. Hänen Laplace -muunnos on antanut:

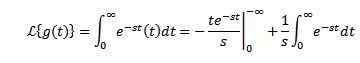
Kun integroitat osilla ja tietäen sen^-Stri Sillä on taipumus 0, kun T: llä on taipumus äärettömyyteen ja S> 0, yhdessä edellisen esimerkin kanssa, joka meidän on:

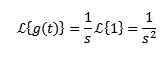
Transformal voi olla tai ei ole, esimerkiksi funktion f (t) = 1/t, integraali, joka määrittelee sen Laplace -muunnoksen.

Riittävät olosuhteet varmistaakseen, että funktion f on Laplace -muunnos, on, että F on jatkuvaa osissa t ≥ 0: lle ja se on eksponentiaalista järjestystä.

Sanotaan, että funktio on jatkuvaa osissa t ≥ 0: lle, kun minkä tahansa välille [a, b]> 0: lla on rajallinen määrä pisteitä t_{k -k -,} Missä F: llä on epäjatkuvuuksia ja se on jatkuvaa jokaisessa alaryhmässä [t_K-1,t_{k -k -}-.

Toisaalta sanotaan, että eksponentiaalinen funktio C, jos on todellisia vakioita m> 0, c ja t> 0, niin:

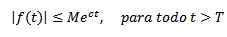
Esimerkiksi meidän on f (t) = t² Se on eksponentiaalinen, koska | t²Ja < e^3T Kaikille t> 0.

Meillä on muodollisesti seuraava lause:

Lause (riittävät olosuhteet)

Jos F on jatkuva toiminto T> 0: lle ja eksponentiaalille C, niin S> C: n Laplace -muunnos on.

On tärkeää korostaa, että tämä on riittävyyden ehto, toisin sanoen, että voi olla olemassa, että on olemassa funktio, joka ei täytä näitä ehtoja, ja silti sen Laplace -muunnos on olemassa.

Esimerkki tästä on funktio f (t) = t^-1/2 joka ei ole jatkuvaa osissa t ≥ 0, mutta sen Laplace -muunnos on olemassa.

Joidenkin perustoimintojen Laplace -muunnos

Seuraava taulukko näyttää yleisimpien toimintojen Laplace -muunnokset.

Voi palvella sinua: kokonaiset numerot

Laplace -muunnon historia

Laplace-muunnos on velkaa nimensä Pierre-Simon Laplace, matemaatikko ja ranskalainen tähtitieteilijä ja teoreetikko, joka syntyi vuonna 1749 ja kuoli vuonna 1827. Hänen maine oli sellainen, että hänet tunnetaan nimellä Newton Ranskassa.

Vuonna 1744 Leonard Euler (1707-1783) omistautui opinnot integraaleille lomakkeen kanssa

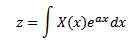
tavallisten differentiaaliyhtälöiden ratkaisuina, mutta hylkäsivät tämän tutkimuksen nopeasti. Myöhemmin Joseph Louis Lagrange (1736-1813), joka ihaili Euleria paljon, tutki myös tämän tyyppistä integraalia ja liittyi ne todennäköisyyden teoriaan.

1782, Laplace

Vuonna 1782 Laplace aloitti näiden integraalien opiskelun ratkaisuina differentiaaliyhtälöihin ja historioitsijoiden mukaan hän päätti vuonna 1785 uudelleenmuokkaamaan ongelman, joka myöhemmin synnytti Laplacen muutokset, kuten ne ymmärretään tänään.

Saatuaan todennäköisyysteorian alalla, se oli vähän kiinnostavaa hetken tutkijoita, ja sitä pidettiin vain matemaattisena kohteena vain teoreettisen mielenkiinnon kohteena.

Heaviside Oliver

Se oli 19. vuosisadan puolivälissä, kun englantilainen insinööri Oliver Heaviside havaitsi, että differentiaalioperaattoreita voidaan käsitellä algebrallisina muuttujina, mikä antaa niiden modernin sovelluksen Laplace Transforms -sovellukseen.

Oliver Heaviside oli fyysikko, englantilainen sähkö- ja matemaattinen insinööri, joka syntyi vuonna 1850 Lontoossa ja kuoli vuonna 1925. Yritettäessä ratkaista värähtelyteoriaan sovellettujen differentiaaliyhtälöiden ongelmat ja Laplace -tutkimusten avulla se alkoi muokata Lapla -muunnosten nykyaikaisia ​​sovelluksia.

Heaviside -paljastamat tulokset levisivät nopeasti.

Heavisidin työn hyödyllisyys fysiikan yhtälöiden ratkaisemisessa aiheutti heidän menetelmänsä olevan suosittu fyysisten ja insinöörien välillä.

Näistä takaiskuista huolimatta ja muutaman vuosikymmenen epäonnistuneiden yritysten jälkeen 1900 -luvun alussa sille voitaisiin antaa tiukka perustelu Heavisidin asettamille operatiivisille säännöille.

Nämä yritykset maksoivat muun muassa erilaisten matemaatikkojen, kuten Bromwichin, Carson, van der Polin ponnistelujen ansiosta.

Laplace -muunnosominaisuudet

Laplace -muunnoksen ominaisuuksista seuraava erottuu:

Lineaarisuus

Olkoon C1- ja C2 -vakio ja F (t) ja G (t) -funktiot, joiden Laplacen muunnokset ovat vastaavasti f (s) ja g (s), niin sen on:

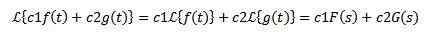
Tämän ominaisuuden takia sanotaan, että Laplace Transform on lineaarinen operaattori.

Esimerkki:

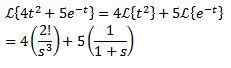
Ensimmäinen käännöslause

Jos tapahtuu, se:

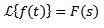
Ja 'A' on sitten oikea numero, sitten:

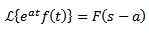
Esimerkki:

Laplace de cos -muunnoksena (2t) = s/(s^2 + 4) sitten:

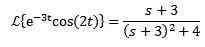
Toinen käännöslause

Joo

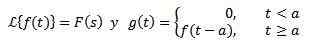
Niin

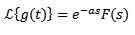
Esimerkki:

Jos f (t) = t^3, niin f (s) = 6/s^4. Ja siksi muutos 

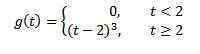
on g (s) = 6e^-2s/s^4

Mittakaava

Joo

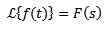
Ja 'a' on todella erilainen kuin nolla, meidän on

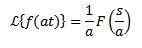
Esimerkki:

Kuten f (t) = sen (t) muunnos on f (s) = 1/(s^2 + 1)

Voi palvella sinua: Kehitetty merkintä: Mikä on, esimerkkejä ja harjoituksia

Laplace muuttui johdannaisista

Jos f, f ', f ", ..., f^(N) Ne ovat jatkuvia t ≥ 0: lle ja ovat eksponentiaalisia ja f^(N)(t) on jatkuvaa osissa t ≥ 0, sitten

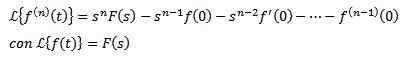
Integral Laplace -muutos

Joo

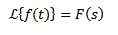
Niin

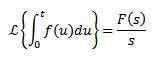
Kertolasku T: lläⁿ

Jos meidän on

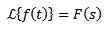
Niin

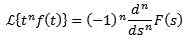
Jako T: llä

Jos meidän on

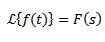
Niin

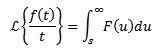
Säännölliset toiminnot

Olkoon f jaksollinen funktio, jolla on jakso t> 0, ts. F (t +t) = f (t), sitten

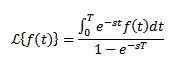
F (S): n käyttäytyminen, kun S: llä on taipumus äärettömyyteen

Jos F on jatkuvaa osissa ja eksponentiaalisessa järjestyksessä ja

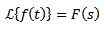
Niin

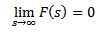
Käänteinen

Kun käytämme Laplace -muunnosta funktioon f (t), saamme F (s), joka edustaa mainittua muunnosta. Samoin voimme sanoa, että f (t) on f (s) käänteisen Laplace -muunnos ja se on kirjoitettu

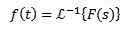
Tiedämme, että f (t) = 1 ja g (t) = T Laplace -muunnokset ovat f (s) = 1/s ja g (s) = 1/s² Siksi meidän on tehtävä

Jotkut muuttuvat yleinen Laplace ovat seuraavat

Lisäksi käänteinen Laplace -muunnos on lineaarinen, ts

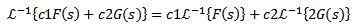
Harjoittele

löytö

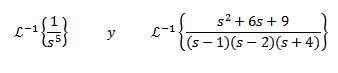
Tämän harjoituksen ratkaisemiseksi meidän on sovittava f (s) -toiminto joidenkin edellisen taulukkojen kanssa. Tässä tapauksessa, jos otamme N + 1 = 5 ja käyttämällä käänteisen muunnoksen lineaarisuusominaisuutta, kerrotaan ja jaamme 4: llä! Saada

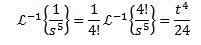
Toiseen käänteiseen muunnokseen käytämme osittaisia ​​fraktioita funktion F (S) ja sitten lineaarisuuden ominaisuuden kirjoittamiseksi, hankkimiseksi

Kuten näistä esimerkeistä voidaan nähdä, on yleistä, että arvioitu funktio F (S) ei vastaa tarkalleen mitään taulukossa annettuja toimintoja. Näissä tapauksissa, kuten havaittiin, se riittää funktion kirjoittamiseen, kunnes se saavuttaa oikean muodon.

Laplace Transform -sovellukset

Differentiaaliyhtälöt

Pääsovellus, jolla Laplace muuntaisi hallussaan, on ratkaista differentiaaliyhtälöt.

Johdannaisen muunnon ominaisuuden avulla on selvää, että

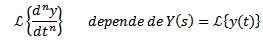
Ja N-1-johdettu arvioitu t = 0.

Tämä ominaisuus tekee muuttuneesta.

Seuraavat esimerkit osoittavat, kuinka Laplace -muunnosta käytetään erotusyhtälöiden ratkaisemiseksi.

Esimerkki 1

Seuraava alkuarvoongelma

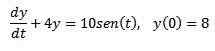
Löydä ratkaisu Laplace -muunnolla.

Käytämme Laplace -muunnosta differentiaaliyhtälön jokaiseen jäseneen

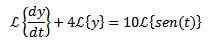
Johdannaisen muunnoksen omaisuudelle

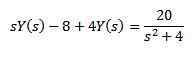
Kehitettäessä kaikkia ilmaisua ja puhdistusta ja (s) meillä on

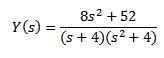
Osittaisten fraktioiden käyttäminen saamamme yhtälön oikean puolen uudelleenkirjoittamiseksi

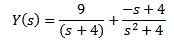
Lopuksi tavoitteemme on löytää funktio ja (t), jotka tyydyttävät differentiaaliyhtälön. Käyttämällä käänteistä Laplace -muunnosta se johtaa

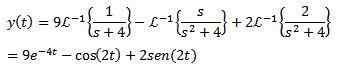
Esimerkki 2

Ratkaista

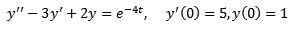
Kuten edellisessä tapauksessa, käytämme muunneltua yhtälön molemmille puolille ja erillinen termi.

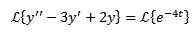
Tällä tavalla meillä on seurauksena

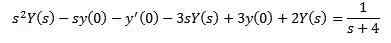
Korvaaminen annetuilla alkuperäisillä arvoilla ja (s) ja (s)

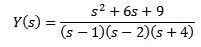
Yksinkertaisten fraktioiden avulla voimme kirjoittaa uudelleen yhtälön seuraavat

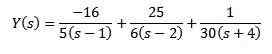
Ja Laplacen käänteisen muunnoksen soveltaminen antaa meille seurauksena

Näissä esimerkeissä voitiin tehdä väärä johtopäätös, että tämä menetelmä ei ole paljon parempi kuin perinteiset menetelmät erotusyhtälöiden ratkaisemiseksi.

Voi palvella sinua: osuus

Laplace -muunnon tarjoamat edut ovat, että se ei ole välttämätöntä.

Lisäksi, kun ratkaistaan ​​alkuperäiset arvoongelmat tällä menetelmällä, käytämme alusta alkaen alkuolosuhteita, joten ei ole tarpeen suorittaa muita laskelmia tiettyjen ratkaisujen löytämiseksi.

Differentiaaliyhtälöjärjestelmät

Laplace -muunnosta voidaan käyttää myös ratkaisujen löytämiseen samanaikaisten tavallisten differentiaaliyhtälöiden kanssa, kuten seuraavassa esimerkissä esitetään.

Esimerkki

Ratkaista

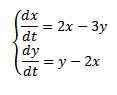
Alkuolosuhteissa x (0) = 8 e y (0) = 3.

Jos meidän on

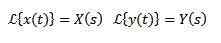
Niin

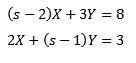
Ratkaiseminen antaa meille seurauksena

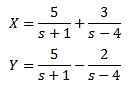
Ja kun käytät Laplacen käänteistä muunnosta

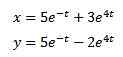
Mekaniikka ja sähköpiirit

Laplace -muunnos on erittäin tärkeä fysiikassa, pääasiassa on sovelluksia mekaniikkaan ja sähköpiireihin.

Yksinkertainen sähköpiiri koostuu seuraavista elementeistä:

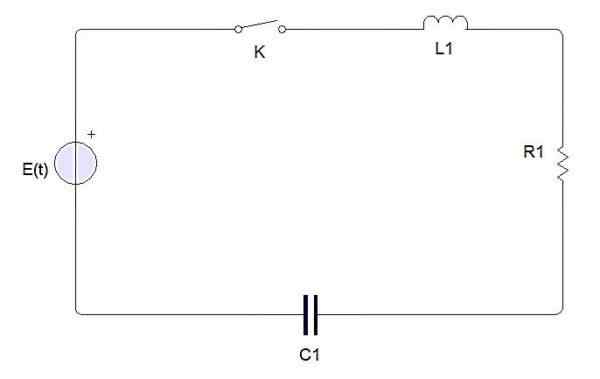Sähköpiirin elementit

Kytkin, akku tai lähde, induktori, vastus ja kondensaattori. Kun kytkin on suljettu sähkövirta, jota I (t) merkitsee. Kondensaattorin kuormitus merkitään q (t).

Kirchhoffin toisen lain mukaan Fuente E: n tuottaman jännitteen on oltava yhtä suuri kuin kunkin jännitteen putoamisen summa.

Sähkövirta I (t) liittyy kondensaattorin kuormaan q (t) i = dq/dt: n kautta. Toisaalta jännitteen pudotus jokaisessa elementissä määritellään seuraavasti:

Jännitteen pudotus vastus on IR = R (DQ/DT)

Induktorin jännitteen pudotus on L (di/dt) = l (D²Q/DT²-A

Jännitteen pudotus kondensaattorissa on q/c

Näiden tietojen avulla ja Kirchhoffin toisen lain soveltamalla yksinkertaiseen yksinkertaiseen piiriin saadaan toisen tilauksen differentiaaliyhtälö, joka kuvaa järjestelmää ja antaa meille mahdollisuuden määrittää Q (t) -arvo.

Esimerkki

Induktori, kondensaattori ja vastus on kytketty akkuun E, kuten kuvassa on esitetty. Induktor. Tällä hetkellä T = 0 sulkee piirin. Etsi kuorma ja virta milloin tahansa t> 0, jos e = 300 volttia.

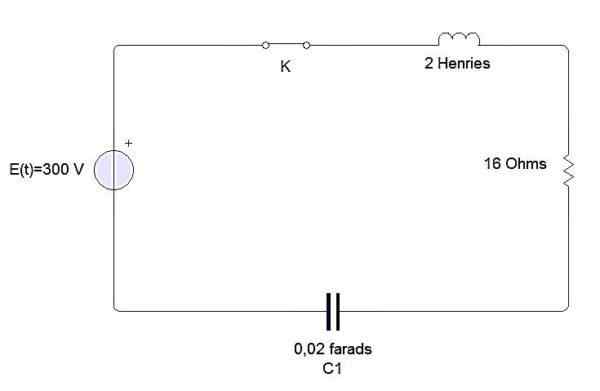
Meillä on, että tätä piiriä kuvaava differentiaaliyhtälö on seuraava:

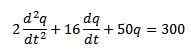
Missä alkuolosuhteet ovat q (0) = 0, i (0) = 0 = q '(0).

Laplace -muunnoksen soveltaminen saamme sen

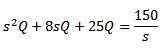
Ja q (t) puhdistaminen

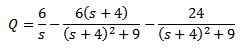
Sitten soveltamalla käänteistä Laplace -muunnosta

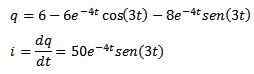
Viitteet

1. G.Holbrook, J. (1987). Laplace -muunnos elektroniikkainsinööreille. Limusa.
2. Ruiz, L. M., & Hernandez, M. P. (2006). Erilaiset ja muunneltut Laplace -yhtälöt sovelluksilla. UPV -toimitus.
3. Simmons, G. F. (1993). Differentiaaliyhtälöt historiallisilla sovelluksilla ja muistiinpanoilla. McGraw-Hill.
4. Spiegel, M. R -. (1991). Laplace muuttui. McGraw-Hill.
5. Zill, D. G., & Cullen, M. R -. (2008). Erotteluyhtälöt arvopapereiden arvojen kanssa rajalla. Cengage Learning Editores, S.-Lla.