Skaaleenikolmio

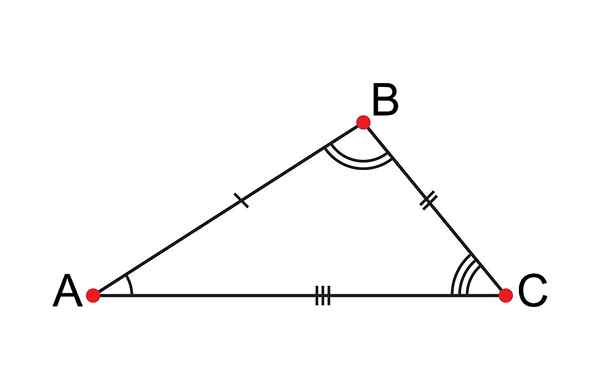
Scallene -kolmiossa on kaikki epätasaiset sivut

Mikä on scallene -kolmio?

Eräs skaaleenikolmio Se on kolmipuolinen monikulmio, jossa jokaisella on erilaisia ​​toimenpiteitä tai pituuksia; Tästä syystä se annettiin escalenon nimi, joka latinalaisessa tarkoittaa epätasa -arvoista.

Kolmiot ovat monikulmioita, joita pidetään geometrian yksinkertaisimpana, koska muodostetaan kolme puolta, kolme kulmaa ja kolme kärkeä. Skaleenikolmion tapauksessa kaikilla eri puolilla se tarkoittaa, että sen kolme kulmaa on myös.

Skaalain kolmioiden ominaisuudet

Asteikko kolmiot ovat yksinkertaisia ​​monikulmioita, koska millään sen sivuilla tai kulmilla ei ole samaa mittaa, toisin kuin tasapainot ja tasapainoteknit.

Koska kaikilla niiden sivuilla ja kulmilla on erilaisia ​​toimenpiteitä, näitä kolmioita pidetään epäsäännöllisinä kuperina monikulmioina.

Sisäisten kulmien amplitudin mukaan skaleenikolmiot luokitellaan seuraavasti:

• Scaleenin suorakulmio kolmio: Kaikki sen sivut ovat erilaisia. Yksi sen kulmista on suora (90^jompikumpi) ja muut ovat akuutteja ja erilaisilla toimenpiteillä.
• Scalene foluse -kolmio: Kaikki sen sivut ovat erilaisia ​​ja yksi sen kulmista on sotku (> 90^jompikumpi-A.
• Scaleena Acutangle -kolmio: Kaikki sen sivut ovat erilaisia. Kaikki sen kulmat ovat akuutteja (< 90^jompikumpi), Erilaisilla toimenpiteillä.

Toinen skaleenikolmioiden ominaisuus on johtuen epäjohdonmukaisista.

Komponentit/elementit

Mediaani

Se on linja, joka lähtee keskipisteestä toiselta puolelta ja saavuttaa vastakkaisen kärjen. Kolme väliainetta osallistuvat pisteeseen nimeltä Baricentro tai Centroid.

Puolustaja

Se on puoliksi oikea. Kolmion puoliarvikkeet ovat kohtaa, jota kutsutaan kannustimeksi.

Mediatrix

Se on segmentti, joka on kohtisuorassa kolmion sivulle, joka on peräisin tämän keskeltä. Kolmiossa on kolme mediaricsia ja osallistuvat kohtaan nimeltään ympärysmittainen.

Korkeus 

Se on linja, joka kulkee kärkipisteestä vastakkaiselle puolelle, ja myös tämä viiva on kohtisuorassa siihen puoleen. Kaikilla kolmioilla on kolme korkeutta, jotka ovat samat pisteet nimeltä Ortotenter.

Escaleno Triangen ominaisuudet

Asteikko kolmiot määritetään tai tunnistetaan, koska niillä on useita niitä edustavia ominaisuuksia, jotka ovat peräisin suurten matemaatikkojen ehdottamista lauseista. He ovat:

Sisäkulmat

Sisäisten kulmien summa on aina yhtä suuri kuin 180^jompikumpi.

Sivujen summa

Kahden osapuolen mittojen summan tulisi aina olla suurempi kuin kolmannen puolen mitta, a + b> c.

Epäyhtenäiset sivut

Kiipeilykolmioiden kaikilla puolilla on erilaiset toimenpiteet tai pituudet; eli ne ovat epäjohdonmukaisia.

Epäyhtenäiset kulmat

Koska skaleenikolmion kaikki sivut ovat erilaisia, sen kulmat ovat myös. Sisäisten kulmien summa on kuitenkin aina yhtä suuri kuin 180º, ja joissain tapauksissa yksi sen kulmista voi olla tylppä tai suora, kun taas toisissa sen kulmat ovat akuutteja.

Voi palvella sinua: moninkertaiset ongelmat lapsille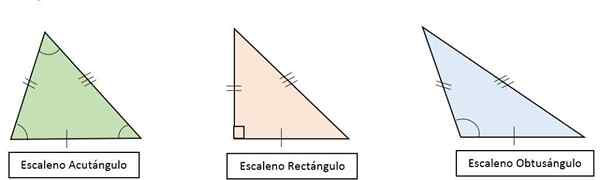 Scalele -kolmiotyypit niiden kulmien mukaan

Korkeus, mediaani, mediarix ja puolustaja eivät ole sattumaa

Kuten mikä tahansa kolmio, Escalenolla on erilaisia ​​linjoja, jotka säveltävät sen, kuten: korkeus, keskipitkä, mediatrix ja bisektori.

Sen sivujen erityisyyden vuoksi tämän tyyppisessä kolmiossa mikään näistä viivoista ei ole samana.

Orocentro, Baricentro, Incentro ja Ympyrä

Kuten korkeus, mediaani, puolustaja ja mediatrix edustaa eri linjasegmentit, Scallene -kolmiossa kokouspisteet -ortokeskuksen, tulkinnan ja ympyränkestävän baricenter -löytyvät eri kohdista (ts. Ne eivät ole yhtä mieltä).

Riippuen siitä, onko kolmio acutlangle, suorakulmio tai tylsä, ortokeskuksessa on eri sijainnit:

-lla. Jos kolmio on acutlangle, ortokeskuksessa on kolmion sisällä.

b -. Jos kolmio on suorakulmio, ortokeskuksessa on samanaikainen suoran puolella olevan kärjen kanssa.

c. Jos kolmio on tylsä, ootokeskuksen ulkopuolella on kolmion ulkopuolella.

Suhteelliset korkeudet

Korkeudet ovat suhteessa sivuihin.

Skaleenikolmion tapauksessa tällä korkeudella on erilaisia ​​toimenpiteitä. Jokaisella kolmiolla on kolme suhteellista korkeutta ja niiden laskemiseksi käytetään Herón -kaavaa.

Kehän laskenta, pinta -ala, korkeus ja sivut

Kuinka kehä lasketaan?

Polygonin kehä lasketaan sivujen summan perusteella.

Kuten tässä tapauksessa Scallene -kolmiossa on kaikki sen sivut eri mittalla, sen kehä on:

P = sivua + sivu B + puoli c.

Kuinka laskea alue?

Kolmiot lasketaan aina samalla kaavalla, kertomalla pohja korkeudella ja jakamalla kahdella:

Alue = (pohja _* H) ÷ 2

Joissain tapauksissa skaleenikolmion korkeutta ei tunneta, mutta matemaatikko Herón ehdotti kaava, jotta voidaan laskea alueen, joka tietää kolmion kolmen puolen mittauksen.

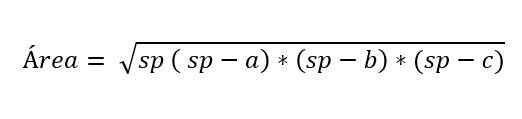
Missä:

• A, B ja C edustavat kolmion sivuja.
• SP vastaa kolmion puolivälissä, ts. Puolet kehästä:

sp = (a + b + c) ÷ 2

Siinä tapauksessa, että vain kaksi kolmion sivua ja niiden välillä muodostettu kulma on, pinta -ala voidaan laskea soveltamalla trigonometrisiä syitä. Siten sinun täytyy:

Alue = (sivu _* H) ÷ 2

Missä korkeus (h) on toisella puolella vastakkaisen kulman läpi. Esimerkiksi kummallakin puolella alue on:

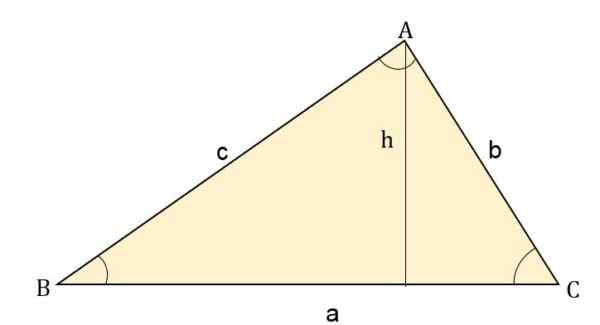
• Alue = (b _* c _* synti a) ÷ 2
• Alue = (a _* c _* synti b) ÷ 2.
• Alue = (a _* b - _* Sen c) ÷ 2

Kuinka laskea korkeus?

Kuten skaleenikolmion kaikki sivut, ne ovat erilaisia, korkeutta ei ole mahdollista laskea Pythagoras -lauseen kanssa.

Herón -kaavasta, joka perustuu kolmion kolmen sivun mittauksiin, alue voidaan laskea.

Voi palvella sinua: tekijän merkinnät: Konsepti, esimerkit ja harjoitukset

Korkeus voi olla selkeä alueen yleisestä kaavasta:

Kaava skaaleenikolmion korkeuden laskemiseksi

Sivu korvataan sivulla A, B tai C.

Toinen tapa laskea korkeus, kun yhden kulman arvo on tiedossa, on trigonometristen syiden soveltaminen, missä korkeus edustaa kolmiota Catoto.

Esimerkiksi, kun vastakkaisen kulman tiedetään korkeudelle, se määritetään rinta:

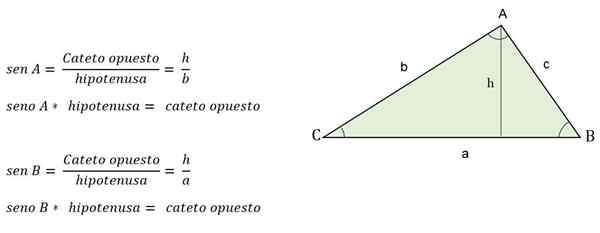Trigonometrinen kaava skaaleeni kolmion korkeuden laskemiseksi

Kuinka laskea sivut?

Kun sinulla on kaksi osapuolta ja kulma, joka vastustaa näitä, on mahdollista määrittää Cosenos -lauseen kolmas puoli.

Esimerkiksi AB -kolmiossa piirretään korkeus verrattuna vaihtovirtasegmenttiin. Tällä tavoin kolmio on jaettu kahteen suorakulmioon.

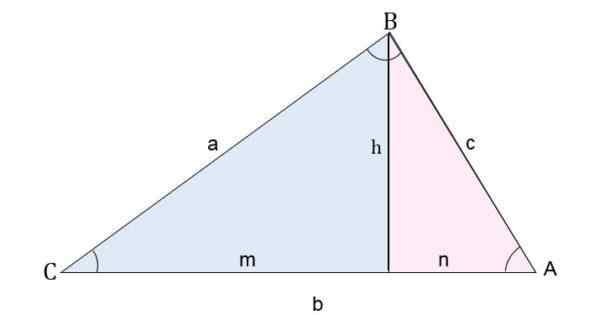Skaleenikolmion jakautuminen kahteen suorakulmioon sivujen laskemiseksi

Sivun C (segmentti AB) laskemiseksi Pythagoras -lause jokaiselle kolmiolle käytetään:

• Siniselle kolmiolle sinun on:

c² = h² + m²

Kuten m = b - n, se korvataan:

c² = h² + b -² (B - n)²

c² = h² + b -² - 2BN + N².

• Vaaleanpunaiselle kolmiolle sinun on:

h² = a² - n²

Se korvataan edellisessä yhtälössä:

c² = a² - n² + b -² - 2BN + N²

c² = a² + b -² - 2 miljardia.

Tietäen, että n = a _* cos c, korvataan edellisessä yhtälössä ja saadaan sivun C -arvo:

c² = a² + b -² - 2b_* -lla _* cos c.

Cosenosin lain mukaan sivut voidaan laskea seuraavasti:

• -lla² = b² + c² - 2b_* c _* tavara.
• b -² = a² + c² - Toinen_* c _* cos b.
• c² = a² + b -² - 2b_* -lla _* cos c.

On tapauksia, joissa kolmion sivujen mittauksia ei tunneta, vaan sen korkeus ja kärjessä muodostuvat kulmat. Alueen määrittämiseksi näissä tapauksissa on tarpeen soveltaa trigonometrisiä syitä.

Tietäen yhden sen kärkipisteiden kulman, luokka tunnistetaan ja käytetään vastaavaa trigonometristä syytä:

Trigonometrinen kaava skaaleenikolmion sivujen laskemiseksi

Esimerkiksi Cateto AB on vastakkainen kulmalle C, mutta kulman a vieressä. Korkeutta vastaavasta sivusta tai jalasta riippuen toinen puoli puhdistetaan tämän arvon saamiseksi.

Ratkaisut

Ensimmäinen harjoitus

Laske Escalano ABC -kolmion alue ja korkeus tietäen, että sen sivut ovat:

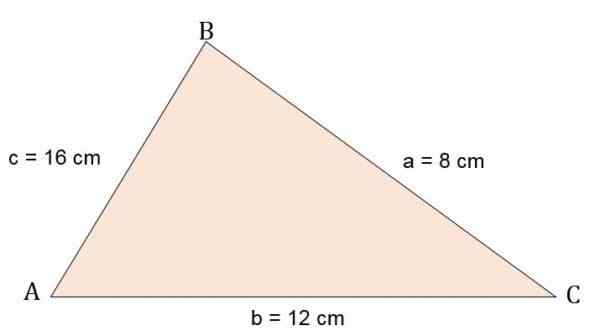
A = 8 cm.

B = 12 cm.

C = 16 cm.

Ratkaisu

Kuten tiedot annetaan skaleenikolmion kolmen puolen mitat.

Koska sinulla ei ole korkeuden arvoa, alue voidaan määrittää soveltamalla Herón -kaavaa.

Ensinnäkin puoliperimetri on laskettu:

sp = (a + b + c) ÷ 2

SP = (8 cm + 12 cm + 16 cm) ÷ 2

SP = 36 cm ÷ 2

SP = 18 cm.

Nyt Herónin kaavan arvot korvataan:

Voi palvella sinua: Absoluuttinen taajuus: kaava, laskenta, jakauma, esimerkki Herón -kaava

Alueen tunteminen voidaan laskea suhteellisen korkeuden sivulle B. Yleisestä kaavasta tyhjentämällä se sinulla on:

Alue = (sivu _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Toinen harjoitus

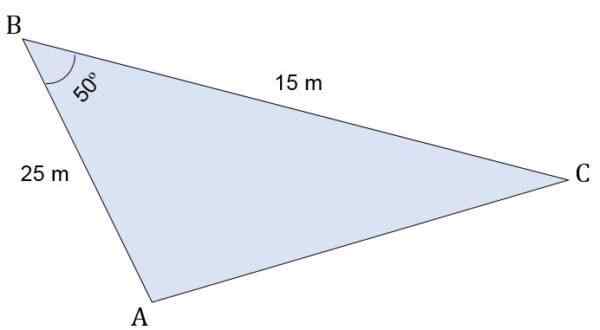
Kun otetaan huomioon ABC Escalano -kolmio, jonka toimenpiteet ovat:

• Segmentti AB = 25 m.
• Segmentti BC = 15 m.

Vertex B: ssä muodostuu 50º kulma. Laske korkeus suhteessa sivulle C, kehä ja kyseisen kolmion pinta -ala.

Ratkaisu

Tässä tapauksessa on kaksi puolustavaa mittaa. Korkeuden määrittämiseksi on tarpeen laskea kolmannen puolen mitta.

Koska vastakkainen kulma annetaan tietyille sivuille, on mahdollista soveltaa Cosenosin lakia AC (B) -puolen mittauksen määrittämiseksi:

b -² = a² + c² - Toinen_*c _* cos b

Missä:

A = bc = 15 m.

C = AB = 25 m.

B = AC.

B = 50^jompikumpi.

Tiedot korvataan:

b -² = (15)² + (25)² - 2_*(viisitoista)_*(25) _* cos 50

b -² = (225) + (625) - (750) _* 0,6427

b -² = (225) + (625) - (482 025)

b -² = 367 985

B = √367 985

B = 19,18 m.

Kuten sinulla on jo kolmen puolen arvo, kyseisen kolmion kehä on laskettu:

P = sivua + sivu B + puoli c

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Alue on nyt mahdollista määrittää soveltamalla Herón -kaavaa, mutta ensin puoliperimetri on laskettava:

sp = p ÷ 2

SP = 59,18 m ÷ 2

SP = 29,59 m.

HERón -kaavan sivujen ja puoliperimetrin mitat korvataan:

Lopuksi, alueen tunteminen, suhteellinen korkeus voidaan laskea sivulle C. Yleisestä kaavasta puhdistamalla se sinun on:

Alue = (sivu _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

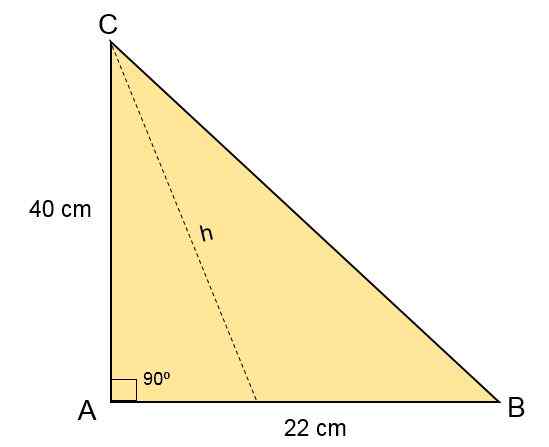
Kolmas harjoitus

Escaleno ABC -kolmiossa B -sivun mitat ovat 40 cm, C -sivun mitat ovat 22 cm ja kärjessä A on 90 kulma^jompikumpi. Laske kyseisen kolmion pinta -ala.

Ratkaisu

Tässä tapauksessa annet.

Alueen määrittämiseksi ei ole tarpeen laskea sivua A.

Koska korkeuden tiedetään vastakkaisesta kulmasta, tämä määritetään toisella puolella olevalla tuotteella ja kulman rinnassa.

Korvaaminen alueen kaavassa sinun on:

• Alue = (sivu _* H) ÷ 2
• H = c _* synti a

Alue = (b _* c _* synti a) ÷ 2

Alue = (40 cm _* 22 cm _* Sen 90) ÷ 2

Alue = (40 cm _* 22 cm _* 1) ÷ 2

Alue = 880 cm² ÷ 2

Alue = 440 cm².

Viitteet

1. Álvaro Rendón,. R -. (2004). Tekninen piirustus: Aktiviteettikirja.
2. Ángel Ruiz, H. B -. (2006). Geometriat. CR -teknologinen, .
3. Enkeli, a. R -. (2007). Perusalgebra. Pearson -koulutus,.
4. Baldor, a. (1941). Algebra. Havana: Kulttuuri.
5. Barbosa, J. Lens. (2006). Litteä euklidinen geometria. Rio de Janeiro,.
6. Coxeter, H. (1971). Geometrian perusteet. Meksiko: limusa-wiley.
7. Daniel C. Alexander, G. M. (2014). Perusgeometria korkeakouluopiskelijoille. Cengage -oppiminen.
8. Harpe, P. d -d. (2000). Geometrisen ryhmäteorian aiheet. University of Chicago Press.