Kolineaalivektorit

Selitämme, mitkä kolineaalivektorit ovat, kolineaalisen vektorijärjestelmän ja laitamme useita esimerkkejä

Mitkä ovat kollineaaliset vektorit?

Se Kolineaalivektorit Ne ovat yksi kolmesta olemassa olevista vektorista. Nämä ovat niitä vektoreita, jotka ovat samaan suuntaan tai toimintalinjaan. Tämä tarkoittaa seuraavaa: Kaksi tai useampaa vektoria on kolineaalinen, jos on olemassa, että ne on järjestetty linjoihin, jotka ovat yhdensuuntaisia ​​toistensa kanssa.

Vektori määritellään runkoon käytettynä suuruutena, ja sille on ominaista suunta, mielessä ja asteikolla. Vektoreita löytyy tasosta tai avaruudesta, ja ne voivat olla erityyppisiä: kolineaalivektorit, samanaikaiset vektorit ja rinnakkaiset vektorit.

Milloin siellä on collineal -vektorit?

Vektorit ovat kolineaalisia, jos yhden toimintalinja on täsmälleen sama toimintalinja kaikkien muiden vektorien riippumatta kunkin vektorin koosta ja suunnasta.

Vektoreita käytetään esityksinä eri alueilla, kuten matematiikka, fysiikka, algebra ja myös geometria, jossa vektorit ovat kolineaalia vain silloin, kun niiden suunta on sama, riippumatta siitä, että niiden merkitys ei ole.

Esimerkkejä kolineaalivektoreista

• Kaksi tai useampaa vektoria on kolineaalinen, jos koordinaattien välinen suhde on sama.

Esimerkki 1

Sinulla on vektoreita m = m_x; m_y ja n = n_x; N_. Nämä ovat kollineaarisia, jos:

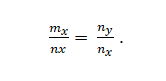
Esimerkki 2

Voidaan määrittää, ovatko vektorit j = 3,6,15 ja p = 1,2,5 kollineaarisia koordinaattien suhteen, jotka sinun on oltava verrannollinen toisiinsa; tarkoittaen: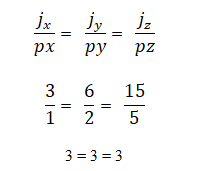

• Kaksi tai useampaa vektoria on kolineaalinen, jos tuote tai vektorikertomus on yhtä suuri kuin nolla (0). Tämä johtuu siitä, että koordinaattijärjestelmässä jokaiselle vektorille on ominaista vastaavat koordinaatit, ja jos nämä ovat verrannollisia toisiinsa, vektorit ovat kollineaarisia. Tämä ilmaistaan ​​seuraavasti:

Voi palvella sinua: vastaavat sarjat: Mitä ovat, selitys, esimerkkejä

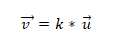
Esimerkki 1

Sinulla on vektoreita a = (10, 5) ja b = (6, 3). Jotta voidaan määrittää, ovatko ne kolineaalisia, sovelletaan määräävää teoriaa, joka vahvistaa ristikkäisten tuotteiden tasa -arvon. Tällä tavalla sinun on:

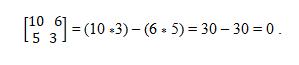
Kolineaalinen vektorijärjestelmä

Colineal -vektorit esitetään graafisesti käyttämällä näiden suunta ja suunnan - pitäen mielessä, että niiden on suoritettava sovelluspiste - ja moduuli, joka on tietty asteikko tai pituus.

Kolineaalisen vektorijärjestelmä muodostuu, kun kaksi tai useampi vektori toimii esineeseen tai runkoon, jotka edustavat voimaa ja toimivat samaan suuntaan.

Esimerkiksi, jos ruumiin kohdistetaan kahta kolineaalista voimaa, tuloksena oleva yksi näistä riippuu vain siitä, missä he toimivat. On kolme tapausta, jotka ovat:

Colineal -vektorit vastakkaisilla aisteilla

Kahden kolineaalisen vektorin tuloksena on yhtä suuri kuin näiden summa:

R = ∑ f = f₁ + F_2.

Esimerkki

Jos kaksi F -voimaa toimivat kärryssä₁ = 40 N ja F₂ = 20 n vastakkaiseen suuntaan (kuten kuvassa esitetään), tulos on:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

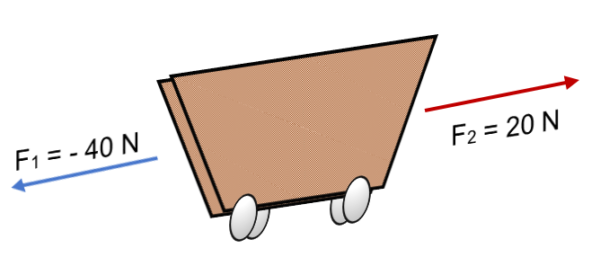Negatiivinen merkki ilmaisee, että vartalo siirtyy vasemmalle, ja voima vastaa 20 N.

Kolineaalivektorit samassa mielessä

Tuloksena olevan voiman suuruus on yhtä suuri kuin kolineaalivektoreiden summa:

R = ∑ f = f₁ + F_2.

Esimerkki

Jos kaksi F -voimaa toimivat kärryssä₁ = 35 N ja F₂ = 55 n samaan suuntaan (kuten kuvassa esitetään), tulos on:

R = ∑ f = 35 n + 55n.

R = 90 N.

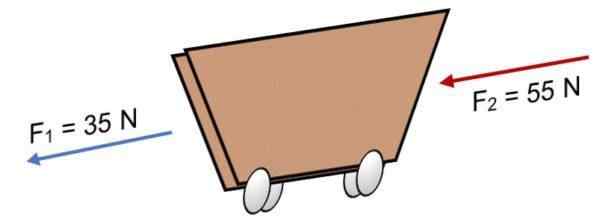
Positiivinen tulos osoittaa, että kollineaalivektorit toimivat vasemmalle.

Se voi palvella sinua: sääntö t: Ominaisuudet, niin että se on esimerkkejä

Colineal -vektorit, joilla on yhtä suuret ja vastakkaiset aistit

Kahden kollineaalisen vektorin tulos on yhtä suuri kuin kollineaaristen vektorien summa:

R = ∑ f = f₁ + F_2.

Koska voimilla on sama suuruus, mutta vastakkaiseen suuntaan -toisin sanoen yksi on positiivinen ja toinen negatiivinen -lisäämällä kaksi voimaa, tulos on yhtä suuri kuin nolla.

Esimerkki

Jos kaksi F -voimaa toimivat kärryssä₁ = -7 N ja F₂ = 7 n, joilla on sama suuruus, mutta vastakkaiseen suuntaan (kuten kuvassa esitetään), tulos on:

R = ∑ f = (-7 n) + 7n.

R = 0.

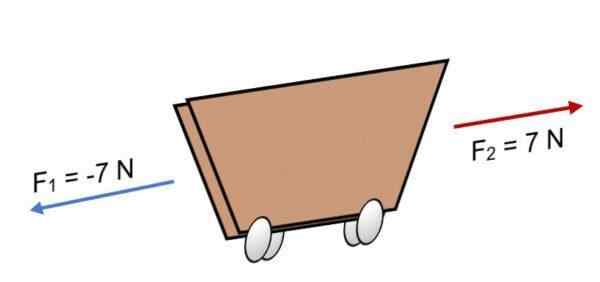
Koska tulos on yhtä suuri kuin 0, se tarkoittaa, että vektorit tasapainovat keskenään ja siksi vartalo on tasapainossa tai lepo (se ei liiku).

Ero kolineaali- ja samanaikaisten vektorien välillä

Colineal -vektoreille on tunnusomaista, että sama suunta on sama linjalla tai koska ne ovat yhdensuuntaisia ​​linjan kanssa; Toisin sanoen ne ovat yhdensuuntaisia ​​linjaohjaajien vektoreita.

Samanaikaiset vektorit puolestaan ​​määritellään, koska ne ovat eri toimintalinjoissa, jotka sieppataan yhdessä pisteessä.

Toisin sanoen, heillä on sama alkuperä- tai saapumispiste -ei -moduulistaan, merkityksestä tai suunnasta -niiden välinen kulma.

Samanaikaiset vektorijärjestelmät ratkaistaan ​​matemaattisilla tai graafisilla menetelmillä, jotka ovat Polygonin rinnakkaisgrammimenetelmä ja menetelmä. Näiden läpi määritetään tuloksena olevan vektorin arvo, joka osoittaa suuntaa, johon runko liikkuu.

Pohjimmiltaan pääasiallinen ero kollineaaristen ja samanaikaisten vektorien välillä on toimintalinja, jossa ne toimivat: kollineaalit toimivat samalla linjalla, kun taas samanaikaiset eri tavalla.

Voi palvella sinua: Yhtälöjärjestelmä: ratkaisumenetelmät, esimerkit, harjoitukset

Toisin sanoen kollineaarivektorit toimivat yhdellä tasolla "x" tai "y"; Ja samanaikainen teko molemmissa lentokoneissa, alkaen samasta kohdasta.

Colineal -vektorit eivät ole yhdessä vaiheessa, kuten samanaikaiset tekevät, koska ne ovat yhdensuuntaisia ​​toistensa kanssa.

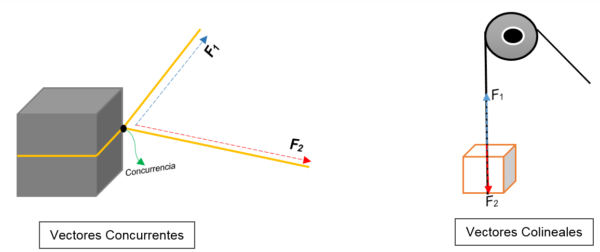
Vasemmassa kuvassa voit nähdä lohkon. Se on sidottu köydellä ja solmu jakaa sen kahteen; Kun löydetään kohti erilaisia ​​suuntauksia ja erilaisia ​​voimia, lohko siirtyy kohti samaa suuntaa.

Kaksi vektoria esitetään yhdessä vaiheessa (lohko) riippumatta niiden moduulista, suunnasta tai suunnasta.

Toisaalta oikeassa kuvassa ilmestyy hihnapyörä, joka nostaa laatikon. Köysi edustaa toimintalinjaa; Kun se keskeytetään, kaksi voimaa (vektoria) vaikuttavat siihen: jännitysvoima (kiipeilyssä lohkoon) ja toinen voima, joka käyttää lohkon painoa. Molemmilla on sama suunta, mutta vastakkaisissa aisteissa; He eivät ole yhtä mieltä yhdessä vaiheessa.