Samanaikaiset vektorien ominaisuudet, esimerkit ja harjoitukset

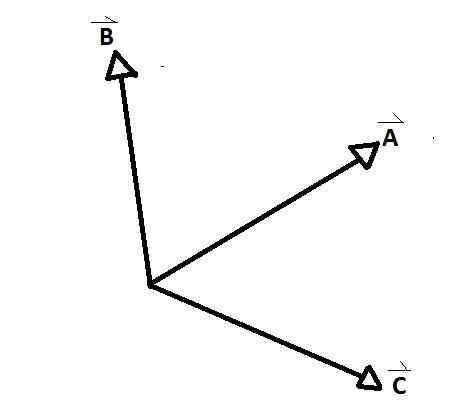
Se samanaikaiset vektorit Ne ovat vektoriryhmiä, joiden akselit ovat yhtä pisteessä, muodostuen kunkin parin välillä sisäinen ja ulkoinen kulma. Alemmassa kuvassa havaitaan selkeä esimerkki, jossa a, b ja c ovat samanaikaisia ​​vektoreita keskenään.

D ja E toisin kuin muut eivät ole. Samanaikaisten vektorien AB, AC: n ja CB: n keskuudessa muodostuu kulmia. Vektoreiden välisiä suhteita kutsutaan.

[TOC]

Ominaisuudet

-Heillä on yhteinen kohta, joka vastaa heidän alkuperänsä: kaikki samanaikaisten vektorien suuruudet alkavat yhteisestä kohdasta heidän omiin ääripäisiin.

-Alkuperää pidetään vektorinäytöspisteenä: on määritettävä toimintakohta, johon jokainen samanaikaiset vektorit vaikuttavat suoraan.

-Verkkotunnuksesi lentokoneessa ja tila on R -² ja r³ Vastaavasti: Samanaikaiset vektorit voivat vapaasti kattaa koko geometrisen tilan.

-Sallii erilaiset merkinnät samassa vektoriryhmässä. Tutkimushaarojen mukaan vektorien operaatioissa esiintyy erilaisia ​​merkintöjä.

Vektorityypit

Vektoreiden haarassa on useita alajakoja, joista joistakin ne voidaan nimittää: rinnakkaiset, kohtisuorat, koplanariot, vastaavat, vastakkaiset ja yhtenäiset. Samanaikaiset vektorit ilmestyvät tähän luetteloon ja kuten kaikki aiemmin nimitetyt, heillä on monia sovelluksia eri tieteissä.

Ne ovat hyvin yleisiä vektoritutkimuksessa, koska ne edustavat kannattavaa yleistämistä heidän kanssaan toiminnassa. Sekä lentokoneessa että avaruudessa samanaikaiset vektorit on tarkoitettu nykyiseen käyttöön eri elementtien esittämisessä ja niiden vaikutusta tiettyyn järjestelmään.

Vektorimerkki

Vektorielementtiä edustaa erilaisia ​​tapoja. Tärkein ja tunnetuimpia ovat:

Karteesilainen

Tämän saman matemaattisen lähestymistavan ehdottama, merkitsee vektoreita, joiden luettelo vastaa kunkin akselin suuruuksia (x, y, z)

V: (1, 1, -1) Avaruus A: (1, 1) Suunnitelma

Napa-

Ne tarkoittavat vain vektoreita tasossa, vaikka olennaisessa laskelmassa syvyyskomponentti osoitetaan. Se koostuu lineaarisella suuruudella r - ja kulma napa -akselin suhteen Ɵ.

Voi palvella sinua: Päätelmätilastot: Historia, ominaisuudet, mitä se on, esimerkkejä

V: (3, 45^{0 -} ) Suunnitelma A: (2, 45^{0 -} , 3) Avaruus

Analyyttinen

Määritä vektorin suuruudet versioiden kautta. Versiot (R & E + K) edustavat akseleita vastaavia yksikkövektoreita X, y ja

A: 3i + 2J - 3K

Pallomainen

Ne ovat samanlaisia ​​kuin polaarinen merkintä, mutta lisäämällä toinen kulma, joka pyyhkäisee tasossa Xy symboloitu Δ.

V: (4, 60^jompikumpi , π/4)

Toiminnot samanaikaisten vektorien kanssa

Samanaikaisia ​​vektoreita käytetään enimmäkseen vektoreiden välisten operaatioiden määrittelemiseen, koska vektorien elementtejä on helpompi verrata samanaikaisesti.

Summa (a + b)

Samanaikaisten vektorien summan tavoitteena on löytää tuloksena oleva vektori V_{r -}. Joka tutkimushaaran mukaan vastaa lopullista toimintaa

Esimerkiksi: 3 merkkijonoa on sidottu a, b, c laatikkoon, köyden jokainen pää on kohteen käsissä. Jokaisen kolmen koehenkilön on vedettävä köysi muuhun suuntaan kuin muut 2.

V: (AX, AY, AZ) B: (BX, BY, BZ) C: (CX, CY, CZ)

A+b+c = (ax+bx+cx; ay+by+cy; az+bz+cz) = V_{r -}

Laatikko voi liikkua vain yhteen suuntaan, siksi V_{r -} osoittaa laatikon siirtymisen suunnan ja merkityksen.

Ero (a - b)

Vektoreiden väliseen eroon liittyy monia kriteerejä, monet kirjoittajat päättävät sulkea sen pois ja väittää, että vain vektorien välinen summa on määrätty, missä ero on vastakkaisen vektorin summa. Totuus on, että algebrallisesti vektorit voidaan vähentää.

V: (AX, AY, AZ) B: (BX, BY, BZ)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]

Skalaarituote (a . B)

Tunnetaan myös nimellä Puto -tuote, tuottaa skalaariarvon, joka voi liittyä useisiin tutkimushaaran mukaan myös useisiin suuruuksiin.

Geometrialle osoittaa samanaikaisten vektorien parin muodostuman rinnakkaisgrammin alueen rinnakkaisohjelman avulla. Mekaanisen fysiikan suhteen määrittelee voiman tekemän työn F Siirtämällä vartaloa etäisyys ΔR.

Se voi palvella sinua: Yhdistetty suhteellisuus: Selitys, kolme yhdistelmäsääntöä, harjoituksia

ѡ = f . ΔR

Kuten nimestä voi viitata, se tuottaa skalaariarvon ja määritellään seuraavasti:

Olla vektorit a ja b

V: (AX, AY, AZ) B: (BX, BY, BZ)

-Analyyttinen muoto:

( . B) = | A |.| B |.Cos θ

Missä θ on molempien vektorien välinen kulma

-Algebrallinen muoto:

( . B) = (kirves.BX + AY.kirjoittanut + AZ.BZ)

Vektorituote (A X B)

Kahden vektorin välinen vektori- tai pistemote määrittelee kolmannen vektorin C sen laatu on kohtisuorassa B - ja C. Fysiikassa määrittelee vektorimomentin τ Pyörimisdynamiikan peruselementti.

-Analyyttinen muoto:

Ja A X B | = | A |.| B |.Synti θ

-Algebrallinen muoto:

(A X B) = = (Kirves . kirjoittanut - ay . bx)- (kirves . BZ - AZ . bx) J - + (Kirves . kirjoittanut - ay . bx) k -k -

-Suhteellinen liike: r_A/b

Suhteellisuuden perusta on suhteellinen liike ja samanaikaiset vektorit ovat suhteellisen liikkeen perusta. Voit päätellä sijainnit, nopeudet ja suhteelliset kiihtyvyydet soveltamalla seuraavia ideoita.

r - _A/b = r_-Lla - r -_{B -}    ; Suhteellinen sijainti b: n suhteen

v _A/b = v_-Lla - v_{B -}  ; Suhteellinen kunnioituksen nopeus B: lle

-lla _A/b = a_-Lla - -lla_{B -}  ; Suhteellinen kunnioitus B: lle

Esimerkkejä: Ratkaisut harjoitukset

Harjoitus 1

Olkoon A-, B- ja C -samanaikaiset vektorit.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Määritä tuloksena oleva vektori V_{r -} = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3b = (-3 (3), -3 (5), -3 (-2) = (-9, -15, 6)

V_{r -} = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_{r -} = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1)))

V_{r -} = (-15, -11, 17)

-Määritä skalaarituote (a . C)

( . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

( . C) = 3

-Laske kulma A: n ja C: n välillä

( . C) = | A |.| C |.Cos θ missä θ on lyhin kulma vektorien keskuudessa

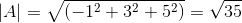
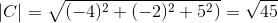
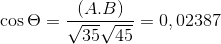
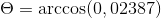
θ = 88,63^{0 -}

 -Etsi vektori kohtisuorassa A ja B

Tätä varten on välttämätöntä määritellä vektorituote (-1, 3, 5) ja (3, 5, -2) välillä. Kuten aiemmin selitettiin, rakennetaan 3 x 3 matriisi, jossa ensimmäinen rivi koostuu yksikkövektorien luettelosta (i, j, k). Sitten toinen ja 3. rivi koostuu käytettävästä vektoreista, jotka kunnioittavat toimintajärjestystä.

Voi palvella sinua: desimaalimerkinnät

(A X B) = = [(-1) . 5 - (3 . 3)] Yllyttää  - [(-1) . (-2) - (5 . 3)] J - + [(-1) . 5 - (3 . 3)] k -k -

(A X B) = (-5 - 9) Yllyttää - (2 - 15) J + (-5 - 9) k -k -         

(A X B) =  -14 I + 13 J - 14 K

Harjoitus 2 

Antaa v_-lla ja v_{b -} Vastaavasti A: n ja B: n nopeusvektorit. Laske B -nopeus a.

V_-lla = (3, -1, 5) V_{b -} = (2, 5, -3)

Tässä tapauksessa B: n suhteellista nopeutta pyydetään V_B/a

V_B/a = V_{B -} - V_-Lla

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

Tämä on a: n Veloc -vektori, joka on nähty a. Jossa b -nopeuden uusi vektori kuvataan viittaamalla A: iin sijoitettuun tarkkailijaan ja liikkuu a: n nopeudella.

Ehdotetut harjoitukset

1-rakenne 3 vektorit A, B ja C, jotka ovat samanaikaisia ​​ja liittyvät 3 toimintaan niiden välillä käytännön harjoituksella.

2 -vektorit A: (-2, 4, -11), B: (1, -6, 9) ja C: (-2, -1, 10). Löydä kohtisuora vektorit: a ja b, c ja b, summa A + B + C.

4-määrää 3-vektoria, jotka ovat kohtisuorassa toisiinsa nähden ottamatta huomioon koordinaattiakseleita.

5-määritelty työn tekemä työ, joka nostaa 5 kg: n massapalon, 20 metrin syvän kaivon pohjasta.

6-swamker-algebrallinen, että vektorien vähentäminen on yhtä suuri kuin vastakkaisen vektorin summa. Perustele postulaatit.

7-Denote a vektori kaikissa tässä artikkelissa kehitetyissä merkinnöissä. (Cartesian, polaarinen, analytiikka ja pallomainen).

8-seuraavat vektorit antavat magneettiin, joka lepää taulukossa lepäämään; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Määritä mihin suuntaan magneetti liikkuu, jos kaikki magneettiset voimat toimivat samanaikaisesti.

Viitteet

1. Euklidinen geometria ja muunnokset. Clayton W. Väistää. Couer Corporation, 1. tammikuuta. 2004
2. Kuinka ratkaista soveltaa matematiikkaongelmia l. Moiseiwitsch. Couer Corporation, 10. huhtikuuta. 2013
3. Geometrian peruskäsitteet. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4. lokakuuta. 2012
4. Vektorit. Rocío Navarro Lacoba, 7. kesäkuuta. 2014
5. Lineaarialgebra. Bernard Kolman, David R. Kukkula. Pearson Education, 2006