Tilavuus

Selitämme, mikä on tilavuus, sen kaavat, yksiköt, kuinka laskea se ja antaa useita esimerkkejä

Mikä on tilavuus?

Hän tilavuus ruumiin on numeerinen arvo, joka mittaa sen miehittämän tilan määrän. Korkea, leveys ja syvyys määrittävät tilavuuden, sitä suurempi, sitä suurempi miehitetty tila.

Tilavuuskonsepti on erittäin tärkeä, koska maailma on kolmiulotteinen ja kaikilla esineillä on leveys, korkeus ja syvyys, siksi niillä on tilavuus. Ihmiset käyttävät sitä usein, esimerkiksi arvioimalla, sopivatko ne huonekalut, se sopii heidän huoneeseensa vai tulevatko he tietyn pukeutumisen koon.

Tietyillä tieteen ja tekniikan aloilla, kuten työskennellessäsi nesteiden kanssa, joko nesteet tai kaasut, miehitetty tilavuus saa suuren merkityksen: kun täytetään astiat ja pumppausnesteet, kuten vettä, tai aluksen suunnittelussa laivan varmistamiseksi, varmistamiseksi Et uppoaa. Kaikki tämä tekee siitä välttämättömän sen määrittämisen monille prosesseille.

Tavallisten muotojen, kuten prismien, pallojen, sylinterien ja kartioiden, geometristen kappaleiden määrän laskemiseksi on olemassa esimerkiksi joistakin sen ulottuvuuksista riippuen. Ja on myös tapoja selvittää epäsäännöllisten esineiden määrä, kuten kuvataan vähän myöhemmin.

Tilavuuskaavat geometrisissa luvuissa

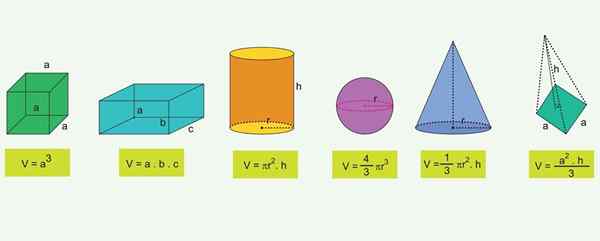Luettelo yleisimmistä geometrisista hahmoista ja niiden tilavuuksien kaavasta

Tunnetuimpien geometristen esineiden saavuttamiseksi on kaavoja, jotka sallivat sen tilavuuden laskemisen:

• Kuutio

V = ℓ³ 

Missä V edustaa tilavuutta ja ℓ on kuution reuna (sivu).

• Suuntaissärmiö

Rinnakkaispiped on suorakaiteen muotoinen laatikko, jonka leveys "A", pitkä ℓ ja "H" -korkeus. Sen tilavuus annetaan sen kolmen ulottuvuuden tuote:

V = a ∙ ℓ h

• Pallo

Pallon tilavuus riippuu sen säteesta r:

Voi palvella sinua: Nicolás Copernico

• Suora pyöreä sylinteri

Suoran pyöreän sylinterin tilavuus on tuote sen pohjan ja sen korkeuden "H" välillä. Koska pohja on radioalbumi “R”, jonka alue on a = π · r², Äänenvoimakkuus pysyy:

V = πr²H

• Pillu

Kartion tilavuus on kolmasosa tuotteesta pyöreän pohjan A pinta -alan ja korkeuden H välillä. Kuten a = πr², niin:

• Pyramidi

Pyramidille, jonka pohjaalue on A ja jolla on korkeus H ”, tilavuus antaa:

Jos pyramidilla on neliöpohja sivulla "A", kuten kuvassa, pohjan pohjapinta -ala on² Ja pyramidin tilavuus on:

V = (1/3) ⋅a²⋅H

• Prisma

Prisman tilavuus on tuote A: n ja korkeuden "H" alueen välillä:

V = a ∙ h

Tilavuusyksiköt

Kansainvälisessä yksikköjärjestelmässä tilavuusyksikkö on kuutiometri tai m³, Anglo -sakson järjestelmässä se on kuutiojalka tai ft³ ( Jalat, joka tarkoittaa englanniksi "jalka").

Miehitetyn tilan koon mukaan on monia muita yksiköitä. Esimerkiksi km kuutiometriä³ Suurempien tilavuuksien tai kuutiometrien millimetrien mm³ Pienille tilalle. On myös paikallisia käyttöyksiköitä.

On myös tarpeen mainita kapasiteettiyksiköt, jotka liittyvät läheisesti tilavuuteen, joita käytetään mieluiten nesteissä. Keskuskapasiteettiyksikkö on litra, lyhennetty L, joka vastaa DM: tä³ (Kuutiometriä).

Muita mainitsemisen arvoisia yksiköitä ovat gallona, ​​kuutio tuumaa, kuppia ja kihtiä, jälkimmäistä käytettiin lääkkeiden annosteluun.

Voi palvella sinua: vertaileva menetelmä

Kuinka tilavuus mitataan?

Kehon tilavuus, kuten mikä tahansa muu mitta, suoritetaan verrattuna riittävään kuvioon, tässä tapauksessa tilavuusyksikkö.

Tilavuusyksikkö määritellään kuutioksi, jonka reuna mittaa 1 yksikkö. Tämä yksikkö voi olla mittari, senttimetri, jalka, tuuma tai mikä tahansa muu. Sitten objektin tilavuus vastaa kuutioyksiköiden määrää ja on aina positiivinen määrä.

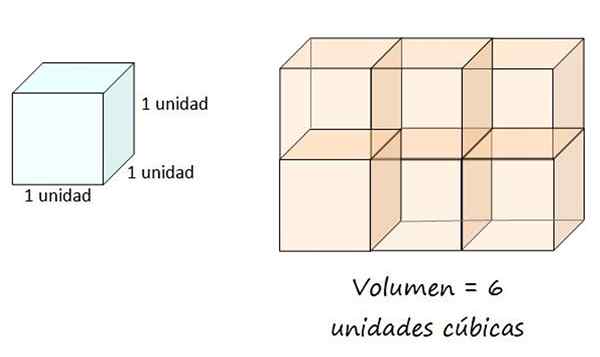Kuubinen yksikkö määritellään kauhan tilavuutena, jonka reuna on yhtä suuri kuin 1, joten oikealla olevassa laatikossa on 6 kuutiometriä. Lähde: f. Zapata.

Geometrisen rungon tilavuus

Kun kyse on geometrisesta rungosta, kuten jo mainittiin, tilavuus lasketaan asianmukaisen kaavan kautta, mitataan kaavalla merkittyjä mittoja.

Esimerkiksi, jos haluat tietää pallon tilavuuden, on tarpeen mitata sen halkaisija ja sen kanssa sen säde on tiedossa, mikä on puoli. Jos se on suorakaiteen muotoinen laatikko, saman leveys, korkeus ja syvyys mitataan.

Sitten kaavassa pyydetyt arvot asetetaan huolehtimaan siitä, että kaikki yksiköt ovat samat, vaadittavat toiminnot suoritetaan, objektin tilavuus.

Epäsäännöllisen rungon tilavuus

Epäsäännöllisillä kiinteillä aineilla ei ole geometristä muotoa, kuten kivi tai silmäily. Silti löydät sen tilavuuden asteittaisen säiliön avulla, joka on täynnä vettä, nesteen siirtymämenetelmän avulla.

Ensinnäkin veden käyttämä tilavuus määritetään ja sitten epäsäännöllinen esine on täysin upotettu, mitataan uusi tilavuus, mikä on suurempi kuin alkuperäinen. Epäsäännöllisen esineen tilavuus on ero tämän tilavuuden ja pelkästään veden tilavuuden välillä.

Voi palvella sinua: Genie Wiley, villi tyttö, joka vain tunnisti nimensä

Jotta tämä menetelmä toimisi, esinettä ei pidä tehdä mistään aineesta, joka on helposti liuennut veteen, sen on pysyttävä täysin upotettuna ja tietysti sinulla on oltava tarvittava koko asteittainen astia, jotta se olisi täysin sijoitettu.

Tilavuusesimerkit

Joidenkin tunnettujen esineiden likimääräinen tilavuus on:

• Maa: 1,08321 × 10¹² km³
• Amazonas -joki: 225.000 m³/S (Aikayksikkötilavuus on nimeltään "Flow")
• Gizan suuri pyramidi: 2.600.000 m³
• Jalkapallopallo: 5600 cm³
• Reppu: 50 DM³

Äänenvoimakkuus

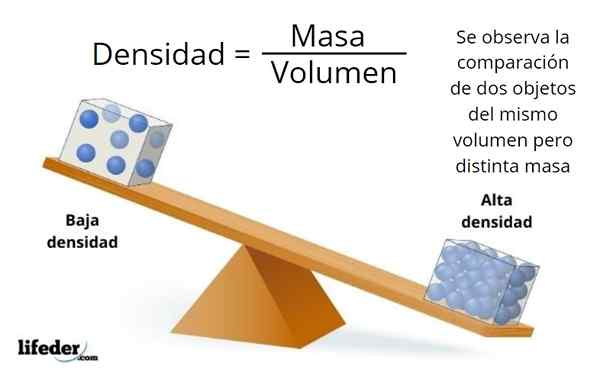
Tilavuus ja massa eivät ole synonyymejä, ensimmäinen on kytketty esineen mittoihin ja toinen sen sisältämää aineen määrää.

Pienten mittojen esineessä voi olla paljon ainetta tai hyvin vähän suuressa esineessä, joka riippuu materiaalin tiheydestä, joka on massan ja esineen tilavuuden välinen suhde:

Ratkaisut

Harjoitus 1

Laske suorakaiteen muotoisen laatikon tilavuus, jonka mitat ovat 34 cm × 22 cm × 8 cm.

• Ratkaisu

Suorakulmaisen laatikon tilavuus on yksinkertaisesti sen kolmen ulottuvuuden tuote:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Harjoitus 2

Neljänneksen pyramidin pohjan pinta -ala on 16 cm² Ja sen korkeus on 6 cm. Laske mainitun pyramidin tilavuus.

• Ratkaisu

Edellä annettua kaavaa pyramidin tilavuudelle käytetään, tunnetaan sen pohjan pinta -ala:

Ja numeeriset arvot korvataan:

V = (1/3) × 16 cm² × 6 cm = 32 cm³