Konjugoidut binomiaaliset miten se on ratkaistu, esimerkkejä, harjoituksia

Eräs Konjugoitu binomiaalinen Toisesta binomialista on sellainen, jossa ne eroavat vain operaation merkistä. Binomiaalinen, kuten nimestä voi päätellä, on algebrallinen rakenne, joka koostuu kahdesta termistä.

Joitakin esimerkkejä binomeista ovat: (A + B), (3M - N) ja (5x - y). Ja heidän vastaavat konjugoidut binomit ovat: (a - b), (-3m - n) ja (5x + y). Kuten heti voidaan nähdä, ero on merkissä.

Kuvio 1. Binomiaalinen ja sen konjugoitu binomiaali. Heillä on samat ehdot, mutta eroavat merkistä. Lähde: f. Zapata.

Binomiaalinen kerrottuna konjugaatinsa perusteella johtaa merkittävään tuotteeseen, jota käytetään paljon algebrassa ja tieteessä. Kertolaskennan tulos on alkuperäisen binomiaalin termien neliöiden vähentäminen.

Esimerkiksi, (X - y) Se on binomiaalinen ja sen konjugaatti on (x + y). Sitten kahden binomin tuote on termien neliöiden ero:

(X - y).(x + y) = x² - ja²

[TOC]

Kuinka konjugoitu binomiaalinen ratkaisu?

Konjugoitujen binomien kanssa mainittu sääntö on seuraava: 

Kahden konjugaattibinomien tuote on yhtä suuri kuin ensimmäisen termin neliö miinus toisen termin neliö. Tätä tulosta kutsutaan neliömäiseksi.

Esimerkkinä sovelluksesta aloitamme osoittamalla edellisen tuloksen, joka voidaan tehdä käyttämällä tuotteen jakautuvaa ominaisuutta algebrallisen summan suhteen.

(x - y) (x + y) = x.x + x.ja ja.X - y.ja

Aikaisempi kertolasku saatiin näiden vaiheiden seurauksena:

- Ensimmäisen binomin ensimmäinen termi kerrotaan toisen ensimmäisen kauden mukaan

- Sitten ensimmäinen ensimmäisestä, toisen toisena

- Sitten toinen ensimmäisestä ensimmäisestä toisesta 

- Lopuksi toisen toisen toisen toisen.

Voi palvella sinua: Vector Algebra

Tehdään nyt pieni muutos kommutatiivisen omaisuuden avulla: ja.x = x.ja. Se pysyy näin:

(x - y) (x + y) = x.x + x.y - x.ja ja.ja

Koska yhtäläisiä termejä on kaksi, mutta muuten (korostettu väri ja korostettu), ne peruutetaan ja yksinkertaistetaan:

(x - y) (x + y) = x.X - y.ja

Lopuksi sovelletaan, että lukumäärän kertominen itsessään vastaa sen nostamista, joten x.x = x² ja myös ja.y = y².

Tällä tavoin edellisessä osassa huomautettu, että sen erojen summan tuote on neliöiden ero:

(X - y).(x + y) = x² - ja²

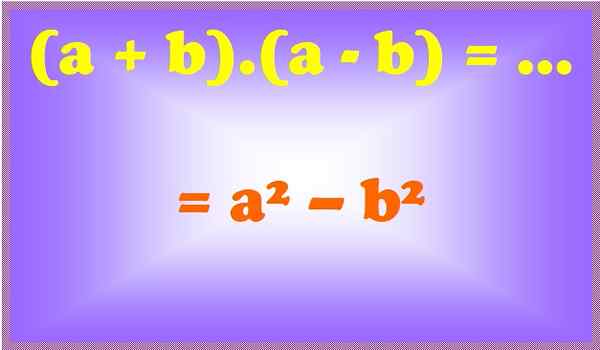Kuva 2. Summa sen erolle on neliöiden ero. Lähde: f. Zapata.

Esimerkit

- Eri lausekkeiden konjugoidut binomit

Esimerkki 1

Löytää konjugaatti (ja² - 3y).

Vastaus: (ja² + 3y)

Esimerkki 2

Hanki tuote (ja² - 3y) konjugaatinsa vuoksi.

Vastaus: (ja² - 3y) (ja² + 3y) = (ja²-A² - (3y)² = y⁴ - 3² ja² = y⁴ - 9y²

Esimerkki 3

Kehitä tuotetta (1 + 2a).(2a -1).

Vastaus: Aikaisempi lauseke vastaa (2A + 1).(2a -1), toisin sanoen se vastaa sen konjugaatin binomin tuotetta.

On tiedossa, että sen konjugoidun binomiaalin binomin tuote on yhtä suuri kuin binomitermien neliöiden ero:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Esimerkki 4

Kirjoita tuote (x + y + z) (x - y - z) neliöerona.

Vastaus: Voimme rinnastaa trinomit ennen konjugoitujen binomien muotoa, hyödyntämällä suluja ja neliöhakeita huolellisesti:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

Tällä tavoin voidaan käyttää neliöiden eroa:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Esimerkki 5

Ilmaista tuote (m² - M -1).(m² + m -1) neliöiden erona.

Voi palvella sinua: 120 jakajaa

Vastaus: Edellinen lauseke on kahden trinomin tuote. Ensinnäkin se on kirjoitettava uudelleen kahden konjugoidun binomials -tuotteena:

(m² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - M].[(M² -1) +m)]

Käytämme sitä tosiasiaa, että sen konjugaatin binomiaalisen tuote on sen termien neliöllinen ero, kuten selitettiin:

[(M² -1) - M].[(M² -1) +m)] = (m² -1)² - m²

Harjoitukset

Kuten aina, se alkaa yksinkertaisimmilla harjoituksilla ja sitten monimutkaisuuden taso on nostamassa.

- Harjoitus 1

Escriba (9 - a²) tuotteena.

Ratkaisu

Ensinnäkin kirjoitamme lausekkeen neliöerona, jotta voimme soveltaa sitä, mitä aiemmin selitettiin. Siksi:

(9 - a²) = (3² - -lla²-A

Me tekijään välittömästi, mikä vastaa tämän neliöeron kirjoittamista tuotteena, kuten lausunnossa pyydetään:

(9 - a²) = (3² - -lla²) = (3 + a) (3 -a)

- Harjoitus 2

Foektoida 16x² - 9y⁴.

Ratkaisu

Tekijä ilmaus tarkoittaa sen kirjoittamista tuotteena. Tässä tapauksessa on välttämätöntä kirjoittaa lauseke uudelleen, neliöeron saamiseksi.

Ei ole vaikeaa tehdä sitä, koska huolellisesti tarkkailemalla kaikki tekijät ovat täydellisiä neliöitä. Esimerkiksi 16 on neliö 4, 9 on neliö 3, ja⁴ on neliö ja² ja x² on neliö X:

16x² - 9y⁴  = 4²x² - 3²ja⁴ = 4²x²  - 3²(ja²-A²

Sitten se, mitä tiedämme jo, sovelletaan: että neliöiden ero on konjugoitujen binomien tuote:

(4x)² - (3 ja²-A² = (4x - 3 ja²-A . (4x + 3 ja²-A

- Harjoitus 3

Kirjoita (a - b) binomiaalisena tuotteena

Ratkaisu

Aikaisempi ero olisi kirjoitettava neliöeroina

(√a)² -(√b)²

Sitten sovelletaan, että neliöiden ero on konjugoitujen binomien tuote

Voi palvella sinua: samanlaisten termien vähentäminen

(√a - √b) (√a + √b)

- Harjoitus 4

Yksi konjugoidun binomin käytöstä on algebrallisten lausekkeiden rationalisointi. Tämä menettely koostuu murto -lausekkeen nimittäjän juurten poistamisesta, joka useaan otteeseen helpottaa operaatioita. Konjugoitua binomia pyydetään käyttämään seuraavan lausekkeen rationalisointia:

√ (2 -x) / [√3 - √ (2+x)]]]

Ratkaisu

Ensimmäinen on tunnistaa nimittäjän konjugoidut binomit: [√3 + √ (2 + x)]]]].

Nyt kerrotaan alkuperäisen lausekkeen numeroija ja nimittäjä konjugoidulla binomilla:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

Edellisen lausekkeen nimittäjässä tunnustamme eron tuote summan perusteella, jonka tiedämme jo, joka vastaa binomien neliöiden eroa:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Nimittäjän yksinkertaistaminen on:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Nyt huolehdimme numeraattorista, jota varten soveltamme tuotteen jakautuvaa ominaisuutta summan suhteen:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

Edellisessä lausekkeessa tunnustamme konjugaatin binomiaalisen (2-x) tuote, joka on merkittävä tuote, joka on yhtä suuri kuin neliöiden ero. Tällä tavoin saadaan lopulta rationalisoitu ja yksinkertaistettu lauseke:

[√ (6-3x) + √ (4-X²)] / (1 - x)

- Harjoitus 5

Kehitä seuraavaa tuotetta konjugoidun binomin ominaisuuksia käyttämällä:

[Toinen^{(x + 3y)} - Kolmas^{(x - 3y)}-.[Toinen^{(x + 3y)} + Kolmas^{(x - 3y)}-

Ratkaisu

Neljäs^{(2x + 6y)} - Yhdeksäs^{(2x - 6y)} = 4a^(2x) .-lla^(6y) - Yhdeksäs^(2x) .-lla^(-6y)= [4a^(6y) - Yhdeksäs^(-6y)- .-lla^(2x)

Huomaavainen lukija on huomannut yleisen tekijän, joka on korostettu värinä.

Viitteet

1. Baldor, a. 1991. Algebra. Venezuelan kulttuuritoimitus S.-Lla.
2. González J. Konjugoituneet binomiaaliset harjoitukset. Toipunut: Akatemia.Edu.
3. Matematiikka Alex. Merkittäviä tuotteita. Palautettu YouTubesta.com.
4. Matematic2me. Konjugoidut binomit/ merkittävät tuotteet. Palautettu YouTubesta.com.
5. Konjugoidut binomiaaliset tuotteet. Palautettu: lms.Colbachenlinea.MX.
6. Vitualinen. Konjugoituja binomials. Palautettu: YouTube.com.