Ilmainen konsepti käsite, yhtälöt, harjoitukset ratkaistu

Se vapaa pudotus Objekti kokee pystysuuntaisen liikkeen, kun se pudotetaan tietystä korkeudesta lähellä maan pintaa. Se on yksi yksinkertaisimmista ja välittöimmistä liikkeistä, jotka tunnetaan: suorassa linjassa ja jatkuvalla kiihtyvyydellä.

Kaikki esineet, jotka pudotetaan tai jotka heitetään pystysuoraan ylös tai alas, liikkuvat kiihtyvyyden ollessa 9.8 m/s² Maan vakavuuden tarjoama massasta riippumatta.

Vapaa pudotus kalliolta. Lähde: Pexels.com.

Tämä tosiasia voidaan hyväksyä tänään ilman ongelmia. Vapaan putoamisen todellisen luonteen ymmärtäminen kesti kuitenkin jonkin aikaa. Kreikkalaiset olivat jo kuvanneet sen ja tulkitsivat hyvin periaatteessa neljännen vuosisadan A c.

[TOC]

Vapaan pudotusliikkeen yhtälöt

Kun olet vakuuttunut siitä, että kiihtyvyys on sama kaikille painovoiman nojalla vapautetuille ruumiille, on aika määrittää tarvittavat yhtälöt tämän liikkeen selittämiseksi.

On tärkeää korostaa, että ilmankestävyyttä ei oteta huomioon tässä ensimmäisen liikkeen mallissa. Tämän mallin tulokset ovat kuitenkin erittäin tarkkoja ja lähellä todellisuutta.

Kaikessa seuraavassa hiukkasmallin oletetaan, toisin sanoen esineen mittoja ei oteta huomioon, olettaen, että koko massa on keskittynyt yhteen pisteeseen.

Tasaisesti kiihdytettyä suoraviivaista liikettä sitä pidetään akselina akseliin ja. Positiivinen merkitys otetaan käyttöön ja negatiivinen.

Kinemaattiset suuruudet

Tällä tavoin sijainnin, nopeuden ja kiihtyvyyden yhtälöt ovat:

Kiihtyvyys

A = g = -9.8 m/s² (-32 jalkaa/s²-A

Sijainti ajasta riippuen: ja T)

y = y_jompikumpi + v_jompikumpi . T + ½ GT²

Missä ja missä ja_jompikumpi Se on matkapuhelimen alkuperäinen sijainti ja v_jompikumpi on alkuperäinen nopeus. Muista.

Se voidaan kirjoittaa seuraavasti:

ja ja_jompikumpi = v_jompikumpi . T + ½ GT²

Δy = v_jompikumpi . T + ½ GT²

Δ: n kanssaja Mobiilihiukkasen tekemä siirtymä. Kansainvälisen järjestelmän yksiköissä sekä asema että siirtymä on annettu metreinä (M).

Nopeus ajasta riippuen: V (t)

V = V_jompikumpi + g . t

Nopeus siirtymästä riippuen

On mahdollista päätellä yhtälö, joka yhdistää siirtymisen nopeuteen ilman väliintuloaikaa. Tätä varten viimeisen yhtälön aika selvitetään:

Voi palvella sinua: Atomin kvantmekaaninen malli

 Ja se korvataan siirtymäyhtälössä:

Δy = v_jompikumpi . T + ½ GT²

Neliö kehitetään merkittävän tuotteen avulla ja termit ryhmittyvät uudelleen.

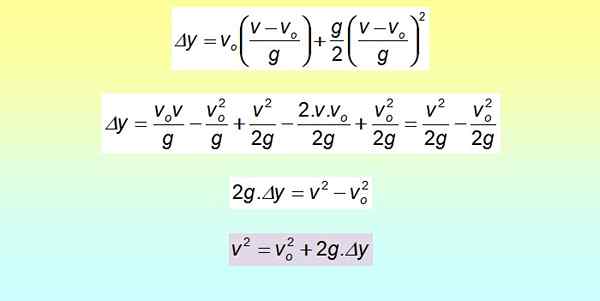
Tämä yhtälö on hyödyllinen, kun aikaa ei ole saatavana, vaan sen sijaan on nopeuksia ja siirtymiä, kuten ratkaistujen esimerkkien osassa nähdään.

Esimerkkejä vapaasta pudotuksesta

Huomaavainen lukija on huomannut alkuperäisen nopeuden V_jompikumpi. Aikaisemmat yhtälöt ovat voimassa pystysuuntaisten liikkeiden kohdalla painovoiman vaikutuksen alla, sekä kun objekti putoaa tietystä korkeudesta, ikään kuin se heitetään pystysuoraan ylös tai alas.

Kun esine putoaa, se on yksinkertaisesti tehty v_jompikumpi = 0 ja yhtälöt yksinkertaistetaan seuraavasti.

Kiihtyvyys

A = g = -9.8 m/s² (-32 jalkaa/s²-A

Sijainti ajasta riippuen: ja T)

y = y_jompikumpi+ ½ GT²

Nopeus ajasta riippuen: V (t)

v = g . t

Nopeus siirtymästä riippuen

v² = 2G. Dy

Dy Se on myös negatiivinen, koska v² Sen on oltava positiivinen määrä. Tämä tapahtuu molemmat, jos alkuperä jompikumpi nolla koordinaattijärjestelmästä laukaisupisteessä tai kentällä.

Jos lukija pitää sitä parempana, se voi viedä suunnan alaspäin positiivisena. Painovoima jatkaa toimintaa, jos ajatellaan, että se on + 9.8 m/s². Mutta sinun on oltava yhdenmukainen valittujen merkintöjen kanssa.

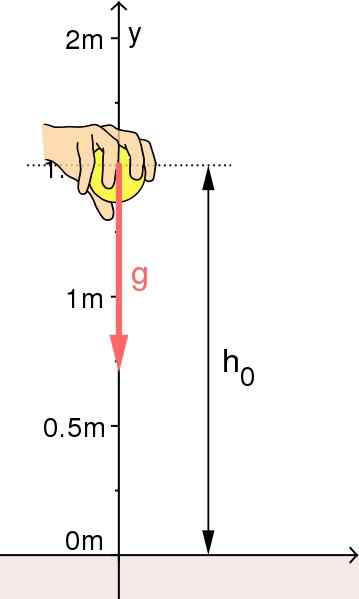Objektin vapaa pudotus: Vertailujärjestelmän alkuperä on valittu maahan. Lähde: Lähde: Mikerun [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)]

Pystysuora käynnistys

Alkuperäinen nopeus ei luonnollisesti voi olla tyhjä. Meidän on annettava kohde impulssille mennä ylös. Annetun alkuperäisen nopeuden mukaan esine nousee suurempaan tai pienempaan korkeuteen.

Tietenkin on hetki, jolloin esine pysähtyy hetkeksi. Silloin maksimikorkeus on saavutettu laukaisupisteeseen nähden. Myös kiihtyvyys on edelleen alas. Katsotaanpa mitä tapahtuu tässä tapauksessa.

Saavutetun enimmäiskorkeuden laskeminen

Valitsemalla minut = 0:

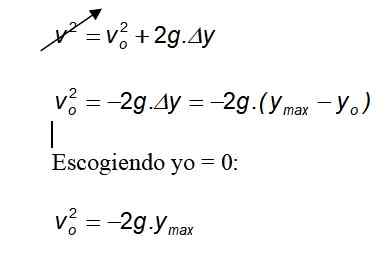
Koska painovoima osoittaa aina maahan negatiiviseen suuntaan, negatiivinen merkki peruutetaan.

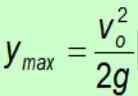
Suurin aikalaskelma

Samankaltainen menettely palvelee löytämään aika, joka kuluu, että objekti saavuttaa enimmäiskorkeuden.

V = V_jompikumpi + g . t

Se tekee V = 0

v_jompikumpi = - g . t_Max

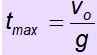
Lentoaika on aika, jolloin esine kestää ilmassa. Jos objekti palaa lähtöpisteeseen, nousuaika on yhtä suuri kuin laskeutumisaika. Siksi lentoaika on 2. T Max.

Voi palvella sinua: Mikroskooppinen asteikko: Ominaisuudet, laskentapartikkelit, esimerkit

On kaksi kertaa t_Max Kokonaisaika, jonka esine kestää ilmassa? Kyllä, niin kauan kuin esine alkaa pisteestä ja palaa siihen.

Jos käynnistys tehdään tietystä korkeudesta maassa ja esineen sallitaan jatkaa tähän, lentoaika ei enää ole kaksinkertainen enimmäismäärään.

Ratkaisut

Seuraavien harjoitusten ratkaisussa seuraavaa otetaan huomioon:

1-korkeus, josta esine pudotetaan, on pieni verrattuna maan säteeseen.

2-Ilmankestävyys on halveksittavaa.

3-Painon kiihtyvyyden arvo on 9.8 m/s²

4-kun se on ongelmia yhdessä matkapuhelimessa, mieluiten se valitaan ja_jompikumpi = 0 lähtökohdassa. Tämä yleensä helpottaa laskelmia.

5-vähemmän kuin päinvastoin on osoitettu, ylöspäin suuntautuva suunta otetaan positiiviseksi.

6 -nousevien ja laskevien yhdistettyjen liikkeiden aikana sovelletut yhtälöt tarjoavat suoraan oikeita tuloksia, kunhan johdonmukaisuus ylläpidetään merkkeillä: ylöspäin, negatiivinen ja vakavuus -9 -arvoinen alaspäin -9.8 m/s² tai -10 m/s² Jos haluat pyöriä (lisää mukavuutta laskettaessa).

Harjoitus 1

Pallo heitetään pystysuoraan nopeudella 25.0 m/s. Vastaa seuraaviin kysymyksiin:

a) kuinka paljon se nousee?

b) kuinka kauan korkeimman pisteen saavuttaminen kestää?

c) Kuinka kauan pallo vie koskettaa maan pintaa, kun se saavuttaa korkeimman pisteensä?

d) Mikä on nopeus, kun palaat tasolle, missä se alkoi?

Ratkaisu

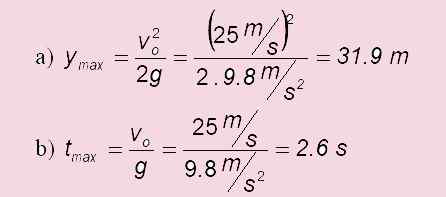
c) Tason lanseerauksen tapauksessa: t_lento = 2 . t_Max = 2 x6 s = 5.1 s

d) Kun se palaa lähtöpisteeseen, nopeudella on sama suuruus kuin alkuperäisen nopeuden, mutta vastakkaisen suunnan, siksi sen on oltava - 25 m/s. Se tarkistetaan helposti korvaamalla arvot yhtälössä nopeuden suhteen:

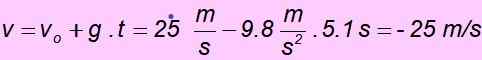
Harjoitus 2

Pieni postimatkustaja vapautetaan helikopterista, joka laskeutuu jatkuvan nopeuden ollessa 1.50 m/s. 2 jälkeen.00 s Laske:

a) Mikä on matkalaukun nopeus?

b) kuinka kaukana matkalaukku on helikopterin alla?

c) Mitkä ovat vastauksesi osioihin a) ja b) Jos helikopteri nousee vakiona nopeudella 1.50 m/s?

Ratkaisu

Osa A

Helikopterista luopuessa matkalaukussa on sen alkuperäinen nopeus, siksi v_jompikumpi = -1.50 m/s. Ilmoitettuna ajankohtana nopeus on lisääntynyt painovoiman kiihtyvyyden ansiosta:

Voi palvella sinua: taivaalliset ruumiit

V = V_jompikumpi + g . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Osa B

Katsotaanpa, kuinka paljon matkalaukku on laskeutunut lähtökohtaan tuolloin:

Matkalaukku: Dy = v_jompikumpi . T + ½ GT² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Se on valittu ja_jompikumpi = 0 Lähtökohdassa, kuten osion alussa osoitetaan. Negatiivinen merkki osoittaa, että matkalaukku on laskeutunut 22. 6 m lähtökohdan alapuolella.

Samaan aikaan helikopteri Se on pudonnut nopeasti -1.50 m/s, oletamme jatkuvasti, siksi ilmoitetun 2 sekunnin ajan, helikopteri on kulkenut:

Helikopteri: δy = v_jompikumpi.t = -1.viisikymmentä x 2 m = -3 m.

Siksi 2 sekunnin kuluttua matkalaukku ja helikopteri erotetaan etäisyydellä:

D =Ja -22.6 - (-3) Ja M = 19. 6 m.

Etäisyys on aina positiivinen. Tämän tosiasian korostamiseksi käytetään absoluuttista arvoa.

Kohta C

Kun helikopteri nousee, sen nopeus on + 1.5 m/s. Tällä nopeudella matkalaukku tulee ulos niin, että 2 s jo kantaa:

V = V_jompikumpi + g . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Nopeus osoittautuu negatiiviseksi, koska 2 sekunnin kuluttua matkalaukku liikkuu alaspäin. On lisääntynyt painovoiman ansiosta, mutta ei niin paljon kuin osassa A.

Nyt löydämme kuinka paljon matkalaukku on laskeutunut lähtökohtaan 2 ensimmäisen matkan aikana:

Valija: δy = v_jompikumpi . T + ½ GT² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Samaan aikaan helikopteri Se on noussut Lähtökohdan suhteen ja tehnyt sen jatkuvalla nopeudella:

Helikopteri: δy = v_jompikumpi.T = +1.viisikymmentä x 2 m = +3 m.

2 sekunnin kuluttua matkalaukku ja helikopteri erotetaan etäisyydellä:

D =Ja -16.6 - (+3) Ja M = 19.6 m

Etäisyys, joka erottaa ne, on sama molemmissa tapauksissa. Matkalaukku kulkee toisessa tapauksessa vähemmän pystysuuntaista etäisyyttä, koska sen alkuperäinen nopeus oli suunnattu ylöspäin.

https: // youtu.be/w2uvetxwsfk

Viitteet

1. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen.  23 - 27.
2. Rex, a. 2011. Fysiikan perusteet. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Osa 1. 50 - 53.
4. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Ed. Cengage -oppiminen. 43 - 55.
5. Wilson, J. 2011. Fysiikka 10. Pearson -koulutus. 133 - 149.