Herkkä lämpökonsepti, kaavat ja harjoitukset ratkaistu

Hän Herkkä lämpö Se on esineeseen syötetty lämpöenergia, joka aiheuttaa sen lämpötilan nousua. Se on piilevän lämmön vastakohta, jossa lämpöenergia ei lisää lämpötilaa, vaan edistää vaihemuutosta, esimerkiksi kiinteästä nesteeseen.

Esimerkki selventää käsitettä. Oletetaan. Kun sijoitamme sen sarveen, toimitettu lämpö nostaa veden lämpötilan hitaasti 100 ° C: seen (veden kiehumislämpötila merenpinnan tasolla). Toimitettua lämpöä kutsutaan herkäksi lämmöksi.

Käsisi lämmittävä lämpö on herkkä lämpö. Lähde: Pixabay

Kun vesi saavuttaa kiehumislämpötilan, Hornillan toimittama lämpö ei enää lisää veden lämpötilaa, joka pysyy 100 ° C: ssa.  Tässä tapauksessa toimitettu lämpöenergia sijoitetaan veden haihtumiseen. Toimitettu lämpö on piilevä, koska se ei nostanut lämpötilaa, mutta aiheutti nestefaasin muutoksen kaasufaasiin.

On kokeellinen tosiasia, että tietyn lämpötilan vaihtelun saavuttamiseksi tarvittava herkkä lämpö on suoraan verrannollinen kyseiseen variaatioon ja esineen massaan.

[TOC]

Käsite ja kaavat

On havaittu, että massa- ja lämpötilaerot lukuun ottamatta herkkä lämpö riippuu myös materiaalista. Tästä syystä herkän lämmön ja massan tuotteen välistä suhteellisuusvakiota lämpötilaeron perusteella kutsutaan erityiseksi lämmöksi.

Toimitetun herkän lämmön määrä riippuu myös prosessin suorittamisesta. Esimerkiksi se on erilainen, jos prosessi suoritetaan vakiotilavuudella kuin vakiopaine.

Kaava herkälle lämmölle prosessissa isobarinen, Toisin sanoen jatkuva paine, se on seuraava:

Q = CP . m (tF - TYllyttää-A

Edellisessä yhtälössä Q - Se on arkaluonteinen lämpö, ​​joka on annettu massaobjektille m, joka on nostanut alkuperäisen lämpötilansa T_Yllyttää Lopulliseen arvoon asti TF. Edellisessä yhtälössä se ilmestyy myös cp, joka on materiaalin erityinen lämpö vakiopaineessa, koska prosessi on suoritettu tällä tavalla.

Huomaa, että herkkä lämpö on positiivinen, kun esine absorboi sen ja aiheuttaa lämpötilan nousun.

Jos prosessi on jäykässä astiassa suljettu kaasu, prosessi on isocorinen, toisin sanoen jatkuvalla tilavuudella; Ja herkkä lämpökaava kirjoitetaan näin:

Voi palvella sinua: aaltoileva liike: ominaisuudet, aaltotyypit, esimerkit

Q = cv. m . (TF - TYllyttää-A

Adiabaattinen kerroin γ

Erityisen lämmön välistä suhdetta vakiopaineessa ja spesifisen lämmön välissä vakiotilavuudella samaan materiaaliin tai aineeseen Adiabaattinen kerroin, joka on yleensä merkitty gamma -gamma -γ -kirjaimella.

Hän Adiabaattinen kerroin on suurempi kuin yksikkö. Lämpö, ​​joka on tarpeen gramman massan lämpötilan nostamiseksi luokkaan on suurempi isobarisessa prosessissa kuin isocoricissa.

Tämä johtuu siitä, että lämmön ensimmäisessä tapauksessa käytetään mekaanista työtä.

Erityisen lämmön lisäksi kehon lämpökapasiteetti määritellään yleensä. Tämä on tarvittava lämpöä kyseisen kehon lämpötilan nostamiseksi celsiusasteen aste.

Lämpökapasiteetti c

Lämpökapasiteetti on merkitty C isot kirjaimet, kun taas erityinen lämpö c pienet kirjaimet. Molempien määrien välinen suhde on:

C = c⋅ m

Missä m Se on kehon massa.

Käytetään myös molaarispesifistä lämpöä, joka on määritelty herkän lämmön määränä, joka tarvitaan nostamaan Celsius- tai Kelvin -lämpötilaan.

Spesifinen lämpö kiinteissä aineissa, nesteissä ja kaasuissa

Useimpien kiinteiden aineiden spesifisen molaarisen lämmön arvo on lähellä 3 ajat R -, missä R - Se on kaasujen yleinen vakio. R = 8,314472 J/(mol ℃).

Esimerkiksi alumiinilla on spesifinen molaarinen lämpö 24,2 J/(Mol ℃), Kupari 24,5 J/(Mol ℃), kulta 25,4 J/(Mol ℃), ja makeaa rautaa 25.1 J/(Mol ℃). Huomaa, että nämä arvot ovat lähellä 3R = 24,9 J/(mol ℃).

Toisaalta useimmille kaasuille erityinen lämpö on lähellä N (r/2), missä on n Kokonaisluku ja R - Se on kaasujen yleinen vakio. Kokonaisluku n liittyy kaasun muodostavan molekyylin vapausasteiden lukumäärään.

Esimerkiksi ihanteellisessa monoatomisessa kaasussa, jonka molekyylissä on vain kolme vapausastetta, spesifinen molaarinen lämpö vakiotilavuuteen on 3 (R/2). Mutta jos se on ihanteellinen diatominen kaasu, kaksi kiertoastetta ovat lisäksi, niin cv = 5 (r/2).

Voi palvella sinua: Puolipyöreä: Kuinka laskea kehä, pinta -ala, keskimmäinen, harjoitukset

Ihanteellisissa kaasuissa seuraavan lämmön molaarisen lämmön ja vakiotilavuuden välinen suhde täyttyy: cp = cv + R -.

Side Maining ansaitsee vettä. Nestemäisessä tilassa 25 ℃ Vesi on cp = 4 1813 J/(G ℃), Vesihöyry 100 asteessa on cp = 2 080 j/(g ℃) Ja vesijää nolla -luokkaan Celsius on cp = 2 050 j/(g ℃).

Ero piilevällä lämmöllä

Ainetta löytyy kolmesta osavaltiosta: kiinteä, nestemäinen ja kaasumainen. Valtion muuttamiseksi tarvitaan energiaa, mutta jokainen aine reagoi siihen eri tavalla sen molekyyli- ja atomiominaisuuksien mukaan.

Kun kiinteä kiinteä sulaa tai neste haihtuu, esineen lämpötila pysyy vakiona, kunnes kaikki hiukkaset ovat muuttaneet sen tilaa.

Siksi on mahdollista, että yksi aine on samanaikaisesti tasapainossa kahdessa vaiheessa: esimerkiksi kiinteä neste tai nestemäinen - höyry - höyry. Määrä ainetta voi kulkea tilasta toiseen lisäämällä tai poistamalla vähän lämpöä, kun taas lämpötila pysyy kiinteänä.

Materiaaliin syötetty lämpö saa sen hiukkasten värähtelyn nopeammin ja lisäämään sen kineettistä energiaa. Tämä tarkoittaa lämpötilan nousua.

On mahdollista, että heidän hankkimansa energia on niin suuri, että he eivät enää palaa tasapainoasentoonsa ja lisäävät erottelua niiden välillä. Kun näin tapahtuu.

Tätä tarvittavassa kuumuudessa se tunnetaan nimellä piilevä lämpö. Siksi piilevä lämpö on lämpöä, jolla aine voi muuttaa vaihetta.

Tässä on ero herkän lämmön kanssa. Aine, joka absorboi herkkiä lämpöä, lisää sen lämpötilaa ja pysyy samassa tilassa.

Kuinka laskea piilevä lämpö?

Piilevä lämpö lasketaan yhtälöllä:

Q = m . Lens

Missä Lens Se voi olla höyrystymisen tai fuusion erityinen lämpö. Yksiköt Lens Ne ovat energiaa/massaa.

Tutkijat ovat antaneet lukuisia lämmön uskontoja riippuen reaktiotyypistä, johon hän osallistuu. Siten esimerkiksi reaktiolämpö, ​​palamislämpö, ​​jähmettymisen lämpö, ​​liuoksen lämpö, ​​sublimaation lämpö ja monet muut.

Voi palvella sinua: Kineettinen energia: Ominaisuudet, tyypit, esimerkit, harjoitukset

Monien näiden lämpötyyppien arvot eri aineille on taulukoitu.

Ratkaisut

Esimerkki 1

Oletetaan, että sellainen on 3 kg massaalumiinia. Aluksi se on 20 ° C: ssa ja haluat nostaa lämpötilansa 100 ° C: seen. Laske tarvittava herkkä lämpö.

Ratkaisu

Ensin meidän on tiedettävä alumiinin erityinen lämpö

cp = 0,897 J / (g ° C)

Joten alumiinin kappaleen lämmittämiseen tarvittava lämmön määrä on

Q = cp m (tf - ti) = 0,897 * 3000 * (100 - 20) J

Q = 215280 J

Esimerkki 2

Laske lämmön määrä, joka tarvitaan 1 litran veden lämmittämiseen 25 ° C - 100 ° C merenpinnan tasolla. Ilmaise tulosta myös kilokaloreilla.

Ratkaisu

Ensimmäinen asia, joka meidän on muistettava, on, että 1 litraa vettä painaa 1 kg, eli 1000 grammaa.

Q = cp m (tf - ti) = 4,1813 j/(g ℃) * 1000 g * (100 ℃ - 25 ℃) = 313597,5 J

Kaloria on energiayksikkö, joka on määritelty herkäksi lämmöksi, joka on tarpeen gramman veden nostamiseksi celsiukselle. Siksi 1 kalori vastaa 4 1813 Joulesia.

Q = 313597,5 J * (1 Cal / 4 1813 J) = 75000 kalkki = 75 kcal.

Esimerkki 3

Kappale 360,16 grammaa materiaalia kuumennetaan välillä 37 ℃ - 140 ℃. Toimitettu lämpöenergia on 1150 kaloria.

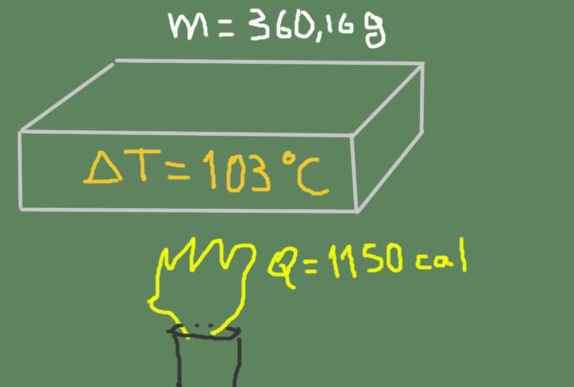Näytteen lämmitys. Lähde: Itse tehty.

Etsi materiaalin erityinen lämpö.

Ratkaisu

Voimme kirjoittaa spesifisen lämmön herkän lämmön, massan ja lämpötilan vaihtelun perusteella kaavan mukaan:

cp = Q /(m Δt)  

Seuraavien tietojen korvaaminen:

cp = 1150 cal / (360,16 g * (140 ℃ - 37 ℃)) = 0.0310 Cal / (G ℃)

Mutta koska kalori vastaa 4 1813 J, tulos voidaan myös ilmaista

cp = 0,130 J / (g ℃)

Viitteet

1. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th. Ed. Prentice Hall. 400 - 410.
2. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 156 - 164.
3. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. Seitsemäs. Tarkistettu painos. McGraw Hill. 350 - 368.
4. Rex, a. 2011. Fysiikan perusteet. Pearson. 309 - 332.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Osa 1. 556 - 553.
6. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Cengage -oppiminen. 362 - 374.