sähkökenttä

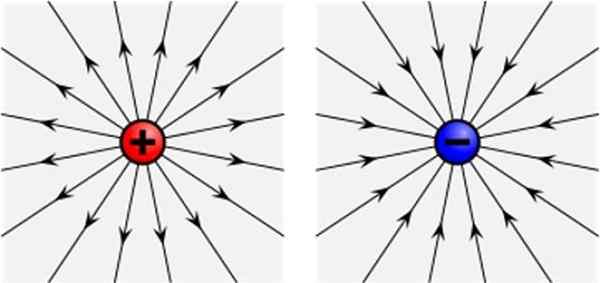
Positiivisen (vasen) ja negatiivinen sähkökenttä (oikea) sähkökenttä (oikea). Lähde: Wikimedia Commons

Mikä on sähkökenttä?

Hän sähkökenttä Se on ominaisuus, jonka ympäröivään tilaan vaikuttavat esineet ovat, jotka muut sähköisesti varautuneet kappaleet kokevat. Mutta toisin kuin kuormien välinen sähkövoima, sähkökenttä riippuu vain sitä tuottavasta kuormasta.

Englantilainen fyysikko Michael Faraday (1791-1867) loi kentän käsitteen havaitsemalla, että mikä tahansa sähkövaraus vaikuttaa sitä ympäröivään tilaan, joten sen ei tarvitse olla kosketuksissa toisen kuorman kanssa, jotta vuorovaikutus tapahtuu.

Ei ole edes välttämätöntä, että kuormat ovat materiaalilaitteessa, koska vuorovaikutus voidaan antaa tyhjiössä.

Oletetaan, että sähkökentän muodon visualisoimiseksi on erityinen ja positiivinen kuorma, nimeltään +Q, jonka koko on niin pieni, että sen mitat eivät ole tarpeen ottaa huomioon. Hänen tuottamansa kenttä pystyy vaikuttamaan muihin maksuihin, kuten toinen positiivinen testipisteen kuorma Q_jompikumpi.

Testikuorma sijoitetaan eri paikkoihin +Q: n ympärille, ja että ne ovat molemmat positiivisia, voima, jota +q käyttää Q: iin_jompikumpi Se on torjuminen.

Piirrä voimajoukko kuormaan Q_jompikumpi Kummassakin sen käytössä olevan tilan kohdassa ja sen poistaminen on joukko viivoja, jotka ilmenevät säteittäisesti kuormasta +Q (katso yllä oleva kuva vasemmalle).

Kun toistat kokemusta negatiivisella kuormalla - Q, myös viivat ovat säteittäisiä, mutta tulevat - q. Molemmissa tapauksissa viivat ovat tangentteja kuorman vektorien sähkökentälle, sen, kun se on positiivinen, ja saapuva, ​​jos se on negatiivinen.

Kaava ja yksiköt

Jos avaruusalueella on sähkökenttä JA, Sähkövaraus q_jompikumpi Kokemus hänelle, voimansa, jonka on antanut:

Voi palvella sinua: Satunnainen virhe: kaava ja yhtälöt, laskenta, esimerkit, harjoitukset

F = q_jompikumpiJA

Jotta:

Kansainvälisen yksikköjärjestelmän sähkökenttäyksikkö on Newton/Coulomb, joka on lyhennetty N/C. On myös yleistä ilmaista sähkökenttä skalaarisen suuruuden suhteen, jota kutsutaan sähköpotentiaaliksi, jolloin kentän kenttä on voltti/metri (V/M).

Täsmällisen kuorman sähkökenttä

Ala JA tuottaa joku esine kuormituksella Q. Koekuorman tekeminen hyvin pieneksi, ts_jompikumpi taipumus 0, vektori JA On:

Kanssa F_jompikumpi q: n ja q: n välinen voima_jompikumpi.

Rajoituksen tarkoituksena on tehdä koekuormasta riittävän pieni, jotta sen kenttä ei muuta sitä, joka haluaa laskea.

Jos mikä on täsmällinen taakka, Coulombin lain mukaan syytteiden Q ja Q välinen voima_jompikumpi, Molemmat erottuvat etäisyyden r, annetaan:

Tässä yhtälössä K on sähköstaattinen vakio ja yksikkövektori linjan suuntaan, joka yhdistää Q ja Q ja Q_jompikumpi On:

Korvaamalla tämän lausekkeen kentän määritelmässä, se saadaan:

 Niin että kenttä JA, Tuotettu täsmällinen kuorma Q pisteessä P, on:

Täten, JA Se ei riipu koekuormasta, vaan sitä tuottavasta kuormasta. Se suuruus kentästä on suoraan verrannollinen kuorman suuruuteen ja käänteisesti verrannollinen kuorman ja pisteen P: n välisen etäisyyden neliöön.

Ja kuten alussa todettiin, osoite Kentältä se on säteittäistä ja suunta on lähtevä kuormaan, kun se on positiivinen, ja saapuva, ​​kun se on negatiivinen.

Sähkökentän voimakkuus

Sähkökenttä on vektori, ja sen voimakkuus viittaa sen moduuliin tai suuruuteen, joka on merkitty ilman rohkeaa. Täsmälliselle kuormitukselle sen sähkökentän voimakkuus on yksinkertaisesti:

Voi palvella sinua: pinnallinen dilaatio: kaava, kertoimet ja esimerkit

 Ja siitä, että se on määrän moduuli, se on aina positiivinen.

Esimerkiksi kuorman tuottaman sähkökentän voimakkuus Q = - 4.3 μC (μC lukee ”mikrokoulomb” ja vastaa miljoonasosista coulombia) 2 cm: n etäisyydellä kuormasta, se on:

Huomaa, että 2 cm: n etäisyydestä tuli metrejä, kertoen voimalla 10⁻², Koska sähköstaattinen vakio on yksiköissä, jos. Ja vaikka kuorma on negatiivinen, sen tuottaman kentän voimakkuus on aina positiivinen, mutta sähkökenttävektori on saapuva kuormaan, kuten aiemmin selitettiin.

Sähkökenttäesimerkit

1. Kuormitusten huomaamaton jakauma sähkökenttä

Joukko tiettyjä maksuja kutsutaan Diskreetti kuormitusjakauma. Tällöin tuloksena oleva sähkökenttä pisteessä P lasketaan soveltamalla Superpositioperiaate, joka on kentän summavektori, jonka kukin kuorma tuottaa p:

JA_netto = JA₁ + JA₂ + JA₃ +..

Seuraava kuva näyttää jakauman, joka koostuu viidestä erityisestä kuormasta ja sähkökentästä, jotka kukin tuottaa kohdassa P:

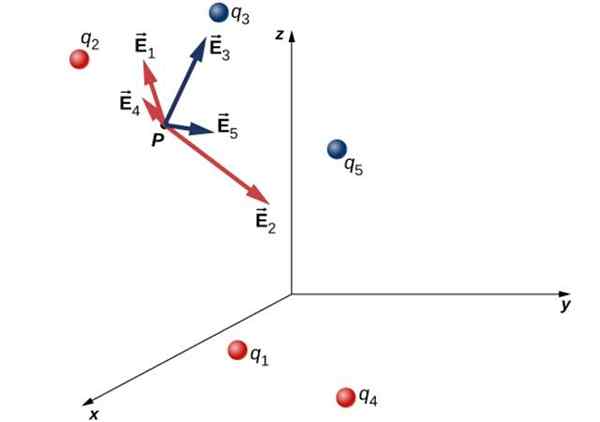Sähkökenttä pisteessä P, kuormitusten huomaamattoman jakautumisen vuoksi

• Kuormat q₃ ja Q₅ Ne ovat negatiivisia ja heidän tuottamansa kenttä on heille saapuva. Ne erotetaan sinisellä.
• Puolestaan, kuormat q₁, Q -₂ ja Q₄ Ne ovat positiivisia, luomalla houkutteleva kenttä punaisella.

2. Jatkuvan kuormitusjakauman sähkökenttä

Jatkuva kuormitusjakauma koostuu laajennetusta esineestä, sähköisesti ladattu, kuten seuraavassa kuvassa esitetty. Koska esineellä on huomattavia ulottuvuuksia, kenttä, jonka osa kehosta tuottaa P: ssä.

Voi palvella sinua: Kirchhoff -lait

Oletetaan, että otetaan pieni sähkövaraus mainitusta esineestä, nimeltään DQ ja oletettu positiiviseksi, mikä tuottaa P: ssä pienen panoksen kokonaiskentän kokonaiskenttään. Tämä panos on sähkökenttävektorin d eroJA.

Koska DQ -kuorma on hyvin pieni, sen kenttä on kuin täsmällinen kuormitus, joten yhtälöä voidaan käyttää ennen kuin näet:

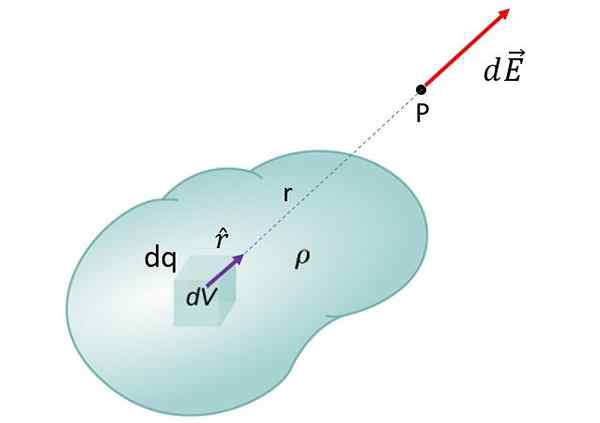Laajennetun objektin sähkökentän laskemiseksi se on integroitu ennen kaikkea. Kuormitustiheys (kuorma tilavuusyksikköä kohti) on merkitty ρ: ksi

Objektin kokonaiskentän saamiseksi pisteessä P on lisätty kaikkien esineiden ottamisen osuuksia. Tämä johtaa olennaiseen:

Liikuntaa

Täsmällinen kuorma q = 2.0 × 10⁻⁸ C sijoitetaan pisteeseen P sähkökentällä, jossa se kokee nousevan voimakkuuden 4.0 × 10⁻⁶ N. Laskea:

a) sähkökenttä p: ssä

b) kuorman q = −1 voima.0 × 10⁻⁸ C sijaitsee P: ssä.

Liittää jhk

Olla sen sähkökentän suuruus, johon kuorma asetetaan. Tämän kentän nojalla tämä kuorma kokee ylöspäin suuntautuvan voimakkuuden F, niin että:

F = q ∙ e

Niin:

E = f /q = 4.0 × 10^-6 N/ 2.0 × 10^-8 C = 200 n/c.

Positiivisella taakalla, voimalla ja kentällä on sama suunta ja merkitys.

Ratkaisu b

Voiman suuruus, joka vaikuttaa: mikä on:

Kun tämä taakka on negatiivinen, voimalla ja kentällä on sama suunta, mutta vastakkaiset aistit.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Nide 2. MC Graw Hill. 
2. Täsmällisen kuorman kenttä- ja sähköpotentiaali. Haettu osoitteesta: SC.Ehu.On.
3. Resnick, r. (1999). Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
4. Sears, z. (2016). Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
5. Yliopistofysiikka. Sähkökenttä. Osa. 2. Haettu osoitteesta: OpenStax.org.