Magneettikentän voimakkuus, ominaisuudet, lähteet, esimerkit

Hän magneettikenttä Se on sähkövarausten liikkumisen vaikutusta ympäröivään tilaan. Kuormilla on aina sähkökenttä, mutta vain liikkeet voivat tuottaa magneettisia vaikutuksia.

Magneettisuuden olemassaolo on ollut tiedossa pitkään. Muinaiset kreikkalaiset kuvasivat mineraalia, joka kykeni houkuttelemaan pieniä rautapaloja: se oli magnette tai magnetiittikivi.

Kuvio 1. Magnetiitinäyte. Lähde: Wikimedia Commons. Rojinegro81 [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Miletus- ja Platonin viisaat miehet huolehtivat kirjoitusten magneettisten vaikutusten rekisteröinnistä; Muuten, he tiesivät myös staattisen sähkön.

Mutta magneettisuus liittyi sähköön vasta 1800 -luvulla, kun Hans Christian Oersted havaitsi, että kompassi oli ohjattu lähellä kuljettajaa kuljettajaa, joka kuljetti virtaa.

Nykyään tiedämme, että sähkö ja magnetismi ovat niin sanotusti saman valuutan kaksi puolta.

[TOC]

Fysiikan magneettikenttä

Fysiikassa, termi magneettikenttä Se on vektorialue, jossa on moduuli (sen numeerinen arvo), suunta avaruuteen ja suuntaan. Sillä on myös kaksi merkitystä. Ensimmäinen on vektori, jota joskus kutsutaan magneettinen induktio Ja se on merkitty B -.

Yksikkö B - Kansainvälisessä yksikköjärjestelmässä on Tesla, lyhennetty T. Toinen suuruus, jota kutsutaan myös magneettikentälle, on H, tunnetaan myös Magneettikentän voimakkuus Ja kenen yksikkö on amperio/metri.

Molemmat suuruudet ovat suhteellisia, mutta ne on määritelty tällä tavalla ottaakseen huomioon magneettiset materiaalit niiden läpi käyville kentille.

Jos materiaali asetetaan ulkoisen magneettikentän keskelle, tuloksena oleva kenttä riippuu tästä ja myös materiaalin magneettisesta vasteesta. Siksi B - ja H Ne liittyvät:

B - = μ_mH

Tässä μ_m  Se on vakio, joka riippuu materiaalista ja jolla on riittävät yksiköt niin, että kertomalla H Tuloksena on Tesla.

Magneettikentän ominaisuudet

-Magneettikenttä on vektorin suuruus, joten sillä on suuruus, suunta ja merkitys.

-Magneettikentän yhtenäisyys B - Kansainvälisessä järjestelmässä se on Tesla, lyhennettynä t, kun taas H Se on ampeeri/mittari. Muita kirjallisuudessa usein esiintyviä yksiköitä ovat Gauss (G) ja Oersted.

-Magneettikenttälinjat ovat aina suljettuja siteitä, jotka poistuvat pohjoisnavasta ja tulevat etelänapaan. Kenttä on aina tangentti viivoille.

-Magneettiset navat näkyvät aina pohjois-etelä-parissa. Eristetty magneettinen napa ei ole mahdollista.

-Se on aina peräisin sähkömaksujen liikkeestä.

-Sen voimakkuus on verrannollinen sen tuottavan kuorman suuruuteen tai virtaan.

-Magneettikentän suuruus pienenee käänteisen etäisyyden neliön kanssa.

-Magneettikentät voivat olla vakioita tai muuttuvia, sekä aikaa että tilaa.

-Magneettikenttä pystyy käyttämään magneettisen voiman liikkuvassa kuormassa tai johdolla, joka virran kuljetus.

Magneetin naput

Baarimagneetissa on aina kaksi magneettista napaa: pohjoisnapa ja etelänapa. On erittäin helppo varmistaa, että yhtä suuret merkin napat hylkäävät, kun taas erityyppiset pylväät houkuttelevat.

Tämä on aivan kuin mitä tapahtuu sähkömaksuilla. Voidaan myös nähdä, että mitä lähempänä he ovat, sitä suurempi voima, jolla he houkuttelevat tai torjuvat.

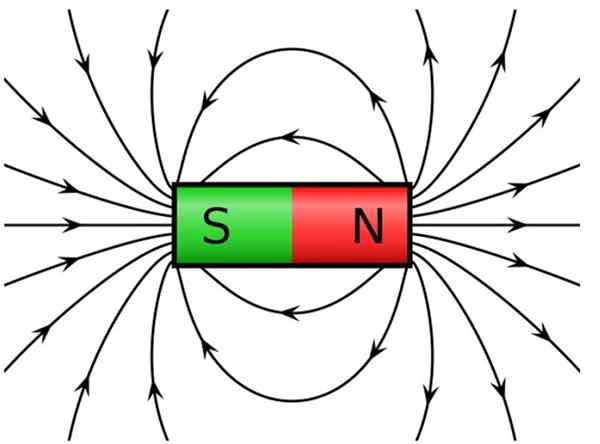
Se voi palvella sinua: Dwarf Galaxy: Koulutus, evoluutio, ominaisuudet, esimerkit

Baarimagneeteilla on erottuva kenttäviivojen kuvio. Ne ovat suljettuja käyriä, jotka poistuvat pohjoisnavasta ja tulevat etelänapaan.

Kuva 2. Baarimagneetin magneettikenttälinjat. Lähde: Wikimedia Commons.

Yksinkertainen kokeilu näiden linjojen tarkkailemiseksi koostuu rautatiedostojen levittämisestä paperiarkin päälle ja alla olevan palkkimagneetin asettamisesta.

Magneettikentän voimakkuus annetaan kenttäviivojen tiheyden mukaan. Nämä ovat aina tiheämpiä pylväiden lähellä ja ulottuvat, kun siirrymme pois magneetista.

Magneetti tunnetaan myös magneettisena dipolina, jossa kaksi napaa ovat juuri pohjoisen ja eteläisen magneettisen pylvään.

Mutta ne eivät voi koskaan erottaa. Jos magneetti leikataan puoliksi, saadaan kaksi magneettia, jokaisella on vastaavat pohjoisen ja eteläisen navansa. Eristettyjä pylväitä kutsutaan Magneettiset monopolit, Mutta tähän mennessä kukaan ei ole pystynyt eristämään.

Lähteet

Voit puhua erilaisista magneettikenttälähteistä. Ne vaihtelevat magneettisista mineraaleista itse maan läpi, joka käyttäytyy kuin suuri magneetti, kunnes saavutat sähkömagneetteja.

Mutta totuus on, että jokaisella magneettikentällä on alkuperäs ladattujen hiukkasten liikkeestä.

Myöhemmin näemme, että kaiken magneettisuuden ensisijainen lähde on pienissä atomin sisällä olevissa virtauksissa, pääasiassa ne, jotka johtuvat ytimen ympärillä olevien elektronien liikkeistä ja atomissa olevien kvanttivaikutusten suhteen.

Sen makroskooppisen alkuperän kannalta voit kuitenkin ajatella luonnollisia lähteitä ja keinotekoisia lähteitä.

Luonnolliset lähteet periaatteessa eivät "sammuta" ovat pysyviä magneetteja, mutta on otettava huomioon, että lämpö tuhoaa aineiden magneettisuuden.

Keinotekoisten lähteiden suhteen magneettinen vaikutus voidaan tukahduttaa ja hallita. Siksi meillä on:

-Luonnolliset magneetit, jotka on valmistettu magneettisista mineraaleista, kuten magnetiitista ja magnetiittisista, molemmat rautaoksidit, esimerkiksi.

-Sähkö- ja sähkömuotoiset virrat.

Magneettiset ja sähkömagneettiset mineraalit

Luonnossa on erilaisia ​​yhdisteitä, joilla on merkittäviä magneettisia ominaisuuksia. He kykenevät houkuttelemaan esimerkiksi rauta- ja nikkelipaloja sekä muita magneetteja.

Mainitut rautaoksidit, kuten magnetiitti ja maghemita, ovat esimerkkejä tällaisista aineista.

Se magneettinen herkkyys Se on parametri, jota käytetään kivien magneettisten ominaisuuksien kvantifiointiin. Perusmallit ovat korkeimmat herkkyydet sen korkean magnetiittipitoisuuden vuoksi.

Toisaalta edellyttäen, että langa on nykyinen, siihen liittyy magneettikenttä. Täällä meillä on toinen tapa luoda kenttä, joka tässä tapauksessa hyväksyy samankeskisten kehän muodon langan kanssa.

Pellon kiertotunne annetaan oikealla peukalon sääntöllä. Kun oikean käden peukalo osoittaa virran suuntaan, loput neljä sormea ​​osoittavat sen merkityksen, jossa kenttäviivat ovat kaareva.

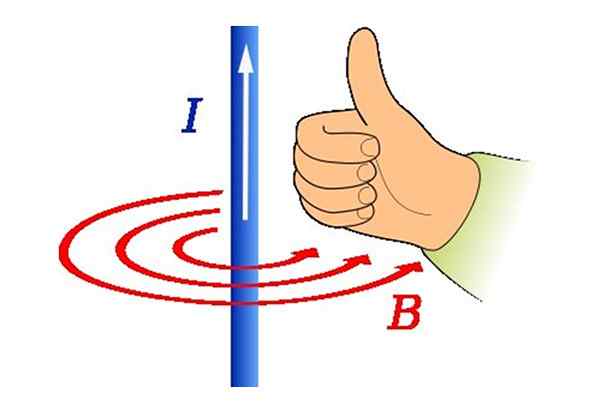Kuva 3. Oikean peukalon sääntö magneettikentän suunnan ja merkityksen saamiseksi. Lähde: Wikimedia Commons.

Sähkömagneetti on laite, joka tuottaa magnetismia sähkövirroista. Sillä on se etu, että se pystyy käynnistämään ja pois päältä. Kun virta lakkaa, magneettikenttä katoaa. Lisäksi kentän voimakkuutta voidaan hallita myös.

Sähkömagnes on osa erilaisia ​​laitteita, joista on puhujia, kiintolevyjä, moottoreita ja releitä.

Voi palvella sinua: oikeanpuoleinen sääntö

Magneettinen voima liikkuvassa varauksessa

Voit tarkistaa magneettikentän olemassaolon B - sähköisen koekuormituksen avulla Q -- Ja se liikkuu nopeudella v. Tätä varten sähkö- ja painovoimakenttien läsnäolo on suljettu pois ainakin tällä hetkellä.

Tässä tapauksessa voima, jota kuorma kokee Q -, joka on merkitty F_{B -}, Se johtuu kokonaan kentän vaikutuksesta. Seuraavaa laadullisesti havaitaan:

-Suuruus  F_{B -}  Se on verrannollinen  Q - Ja nopeudella v.

-Joo v on yhdensuuntainen magneettikentän vektorin, suuruus F_{B -} Se on nolla.

-Magneettinen voima on kohtisuorassa molemmille v Kuten B -.

-Lopuksi magneettisen voiman suuruus on verrannollinen synti θ, olemus θ Nopeusvektorin ja magneettikentän vektorin välinen kulma.

Kaikki yllä olevat ovat päteviä sekä positiivisille että negatiivisille kuormille. Ainoa ero on, että magneettisen voiman merkitys on päinvastainen.

Nämä havainnot ovat yhtä mieltä vektorituotteen kanssa kahden vektorin välillä, niin että täsmällinen kuormitus kokenut magneettinen voima Q -, Se liikkuu nopeudella v Magneettikentän keskellä se on:

F_{B -} = q v x B -

Kenen moduuli on:

F_{B -} = q.v.B -.synti θ

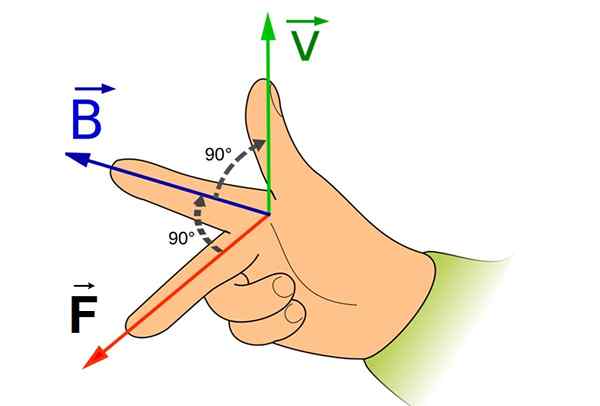Kuva 4. Oikeanpuoleinen sääntö magneettisen voiman positiivisessa täsmällisessä kuormassa. Lähde: Wikimedia Commons.

Kuinka magneettikenttä syntyy?

Esimerkiksi on useita tapoja:

-Sopivan aineen avulla.

-Sähkövirran kuljettamisen kuljettajan kautta.

Mutta magneettisuuden alkuperä selitetään muistamalla, että se on liitettävä kuormien liikkeeseen.

Ydin kiertävä elektroni on pohjimmiltaan pieni virran suljettu piiri, mutta kykenee vaikuttamaan olennaisesti atomin magneettisuuteen. Magneettisen materiaalin pala on monia elektroneja.

Tätä panosta atomin magneettisuuteen kutsutaan Kiertoradan magneettinen hetki. Mutta on enemmän, koska käännös ei ole elektronin ainoa liike. Tällä on myös Spinin magneettinen hetki, kvanttivaikutus, jonka analogia on sen akselin elektronien kierto.

Itse asiassa Espínin magneettinen hetki on atomin magneettisuuden tärkein syy.

Kaverit

Magneettikenttä kykenee omaksumaan monia muotoja siitä peräisin olevien virtausten jakautumisesta riippuen. Se puolestaan ​​voi vaihdella paitsi avaruudessa, myös ajassa tai molemmat samanaikaisesti.

-Sähkömagneetin napojen läheisyydessä on suunnilleen vakiokenttä.

-Myös solenoidin sisällä saadaan korkea intensiteetti ja tasainen kenttä, kenttäviivat on suunnattu aksiaaliakselia pitkin.

-Maapallon magneettikenttä on melko hyvin palkkamagneetin kentälle, etenkin pinnan läheisyydessä. Lisäksi aurinko tuuli muuttaa sähkövirtoja ja muodostaa sen merkittävästi.

-Virtaa kuljettavalla johdolla on kenttä samankeskisten kehän muodossa langan kanssa.

Mitä kenttä voi vaihdella ajoissa, heillä on:

-Staattiset magneettikentät, kun niiden suuruus tai suuntaansa eivät muuttuneet ajan myötä. Baarimagneetin kenttä on hyvä esimerkki tämän tyyppisestä kentästä. Myös ne, jotka ovat peräisin kiinteistä virroista kuljettavista johdoista.

-Muuttuvat kentät ajan myötä, jos jokin sen ominaisuuksista vaihtelee ajan myötä. Yksi tapa saada ne on vuorottelevista virran generaattoreista, jotka hyödyntävät magneettista induktioilmiötä. Niitä löytyy lukuisista yleisen käytön laitteista, esimerkiksi matkapuhelimista.

Voi palvella sinua: Tuloksena oleva vektori: Laskenta, esimerkit, harjoitukset

Biot-Savart-laki

Kun virtojen jakautumisen tuottaman magneettikentän muoto on laskenut, biot-savalakia voidaan käyttää, ja ranskalaiset fyysikot Jean Marie Biot (1774-1862) ja Felix Savart (1791-1841) voidaan löytää vuonna 1820 vuonna 1820.

Joidenkin nykyisten jakautumisten kanssa yksinkertaisilla geometrioilla voidaan saada matemaattinen ekspressio magneettikentän vektorille suoraan.

Oletetaan DL joka kuljettaa sähkövirran Yllyttää. Oletetaan myös, että lanka on tyhjiössä. Magneettikenttä, joka tuottaa tämän jakauman:

-Vähenee käänteisen etäisyyden neliön kanssa.

-Se on verrannollinen virran voimakkuukseen Yllyttää Se kulkee langalla.

-Osoitteesi on tangentiaalinen radion ympärysmitta r - Keskittynyt johtimeen ja sen merkitys annetaan oikealla peukalon sääntöllä.

Nämä havainnot yhdistetään seuraavassa lausekkeessa:Suhteellisuusvakio on Tyhjiöläpäisevyys μ_jompikumpi, jolla se saadaan:Missä:

-μ_jompikumpi = 4π. 10^-7 T.m/ a 

-d -dB - Se on magneettikentän ero.

-Yllyttää Virtakierron voimakkuus on virran voimakkuus.

-r - Se on langan keskuksen ja pisteen välinen etäisyys, josta haluat löytää kentän.

-d -dlens Se on vektori, jonka suuruus on differentiaalisegmentin pituus DL.

-r - Vektori siirtyy langasta pisteeseen, jossa haluat laskea kentän.

Esimerkit

Alla on kaksi esimerkkiä magneettikentästä ja niiden analyyttisistä lausekkeista.

Magneettikentä

Keinoin. Kun tehdään integraatio kuljettajaa pitkin ja ottaen rajatapauksen, jossa tämä on erittäin pitkä, kentän suuruus tulokset:

 Vektorin B suunta ja suunta on merkitty oikean peukalon sääntöllä, kuten voidaan nähdä kuvasta 3.

Helmholtzin kelan luoma kenttä

Helmholtz -kela muodostuu kahdella identtisellä ja samankeskisellä pyöreällä kelalla, jotka sama virta ohitetaan. Niiden on luotu suunnilleen tasainen magneettikenttä sisälle.

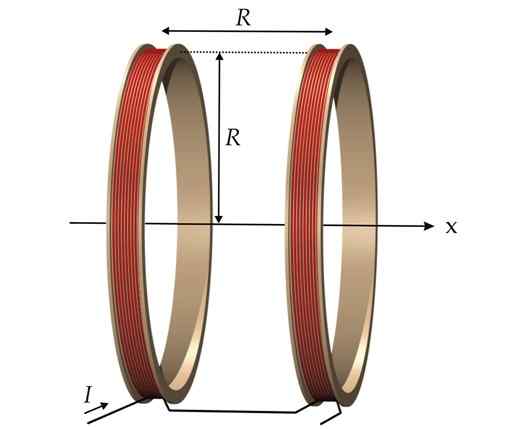Kuva 5. Helmholtz -kelajärjestelmä. Lähde: Wikimedia Commons.

Hänen voimakkuus kelan keskellä on:

Ja on suunnattu aksiaaliakselia pitkin. Yhtälön tekijät ovat:

-N edustaa kelojen käännösten lukumäärää

-Yllyttää Se on virran suuruus

-μ_jompikumpi Se on tyhjiön magneettinen läpäisevyys

-R - Se on kelojen säde.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
2. Magneettikentän voimakkuus H. Palautettu: 230NSC1.Phy-Astr.GSU.Edu.
3. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. Kuudes lyhennetty painos. Cengage -oppiminen.
4. Magneettikenttä ja magneettiset voimat. Toipunut: fysiikka.UCF.Edu.
5. Rex, a. 2011. Fysiikan perusteet. Pearson.
6. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Nide 2. Seitsemäs. Ed. Cengage -oppiminen.
7. Vigon yliopisto. Esimerkkejä magnetismista. Haettu osoitteesta: kvintans.verkkosivustot.Uvigo.On