Vektorimäärät

Mitkä ovat vektorimäärät?

Se Vektorisuure, tai vektoria, jota varten on tarpeen määrittää sekä sen suuruus tai moduuli (vastaavien yksiköiden kanssa) että sen osoite.

Toisin kuin vektorimääritys, skalaarisella määrällä on vain suuruusluokka (ja yksiköt), mutta ei osoitetta. Joitakin esimerkkejä skalaarisista määristä ovat lämpötila, esineen tilavuus, pituus, massa ja aika, muun muassa.

Ero vektorimäärän ja kiipeilyn välillä

Seuraavassa esimerkissä voit oppia erottamaan skalaarimäärän vektorimäärästä:

Nopeus 10 km/h on skalaarinen määrä, kun taas nopeus 10 km/h pohjoiseen on vektorimäärää. Ero on siinä, että toisessa tapauksessa osoite määritetään suuruuden lisäksi.

Vektorimäärillä on ääretön sovellukset, etenkin fysiikan maailmassa.

Grafiikka ja vektorimäärän merkinnät

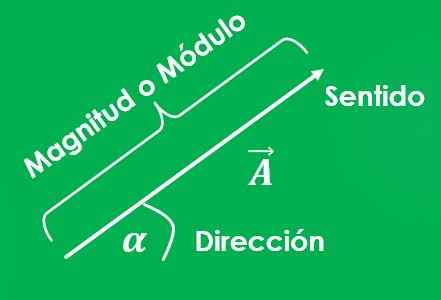
Tapa osoittaa vektorimäärää on asettamalla nuoli (→) käytettävään kirjeeseen tai kirjoittamalla kirjain lihavoituna (-lla-A.

Vektorimäärän kuvaamiseksi tarvitaan vertailujärjestelmä. Tässä tapauksessa Cartesian -tasoa käytetään vertailujärjestelmänä.

Vektorin kuvaaja on viiva, jonka pituus edustaa suuruutta; ja mainitun viivan ja X -akselin välinen kulma, mitattu anti -horary -merkityksessä, edustaa sen osoitetta.

On määritettävä, mikä vektorin lähtökohta on ja mikä on saapumishinta. Nuoli sijoitetaan myös sen linjan loppuun, joka osoittaa saapumispisteeseen, mikä osoittaa, mikä vektorin suunta on.

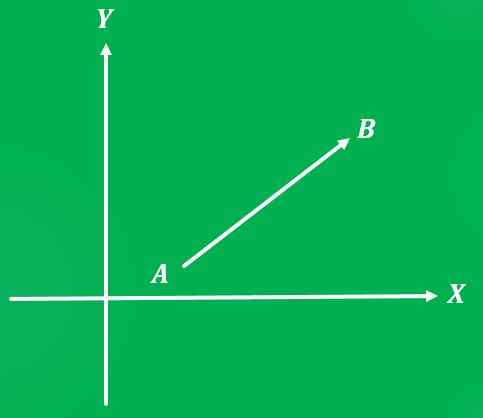
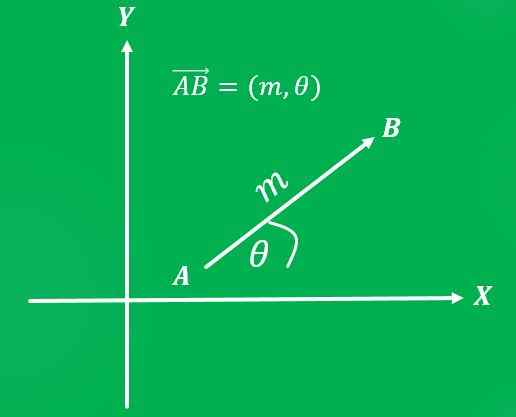
Kun referenssijärjestelmä on asetettu, voit kirjoittaa vektorin järjestäytyneeksi pariksi: ensimmäinen koordinaatti edustaa sen suuruutta ja toinen koordinaatti sen osoite.

Esimerkkejä vektorimääristä

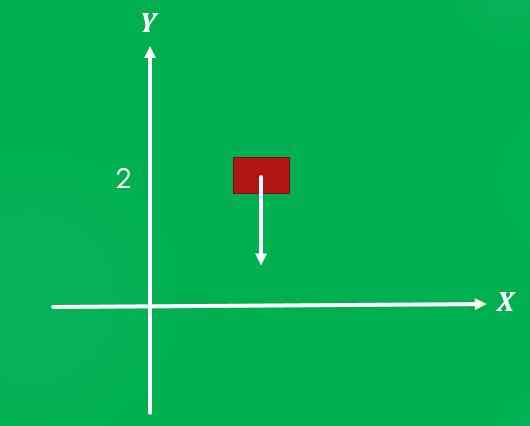
1- esineeseen vaikuttava painovoima

Jos esine sijoitetaan 2 metrin korkeuteen maanpinnan yläpuolelle ja se vapautuu, painovoima vaikuttaa siihen, suuruudella 9,8 m/s² ja suunta kohtisuorassa maahan suuntaan nähden.

2- lentokoneen liike

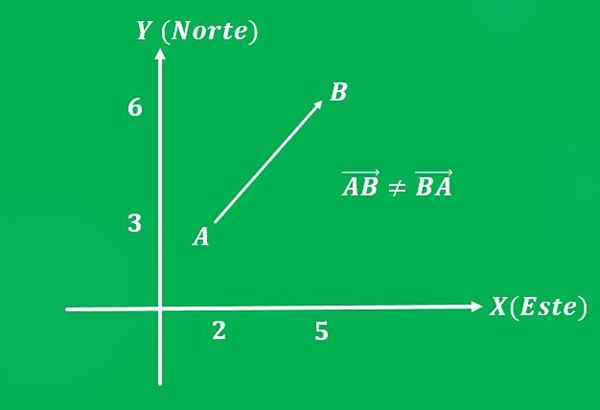
Taso, joka siirtyi pisteestä A = (2,3) pisteeseen B = (5,6) Cartesian -tasosta, nopeudella 650 km/h (voimakkuus). Laitteen suunta on 45 ° koilliseen (tarkoittaen).

On huomattava, että jos järjestys käännetään, niin vektorilla on sama ja sama suunta, mutta erilainen merkitys, joka on lounaaseen.

3- Objektiin kohdistuva voima

Juan päättää työntää tuolin 10 kilon voimalla, maan suuntainen suuntaa. Käytetyn voiman mahdolliset aistit ovat: vasemmalla tai oikealla (Cartesian tason tapauksessa).

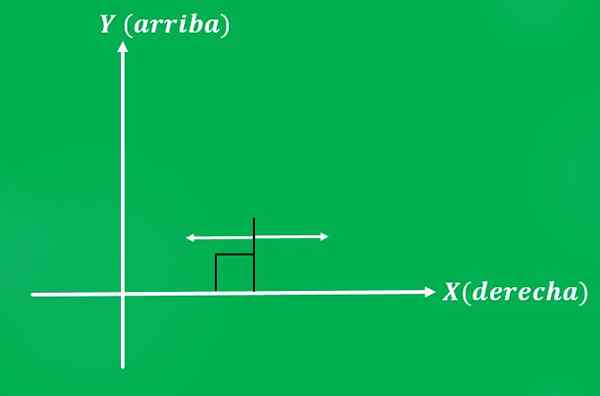
Samoin kuin edellisessä esimerkissä, merkitys, että Juan päättää antaa voiman, tuottaa erilaisen tuloksen.

Tämä kertoo meille, että kahdella vektorilla voi olla sama suuruus ja suunta, mutta ole erilainen (tuottaa erilaisia ​​tuloksia).

Kaksi tai useampaa vektoria voidaan lisätä ja vähentää, joille on erittäin hyödyllisiä tuloksia, kuten rinnakkaisohjelma laki. Voit myös kertoa vektori skalaarilla.