Joustamattomat yhteenotot ulottuvuudessa ja esimerkeissä

Se Joustamattomat iskut tai joustamattomat törmäykset ovat lyhyt ja voimakas vuorovaikutus kahden esineen välillä, joissa liikkeen määrä säilyy, mutta ei kineettisen energian välillä, joista prosenttiosuus muuttuu muun tyyppiseksi energiaksi.

Iskut tai törmäykset ovat luonteeltaan usein. Subatomiset hiukkaset törmäävät erittäin suurilla nopeuksilla, kun taas monet urheilulajit ja pelit koostuvat jatkuvista törmäyksistä. Jopa galaksit kykenevät törmäämään.

Kuvio 1. Koesauton törmäys. Lähde: Pixabay

Oikeastaan ​​liikkeen määrä säilyy minkä tahansa tyyppisissä törmäyksissä, kunhan hiukkaset törmäävät eristetyllä järjestelmällä. Joten tässä mielessä ei ole mitään ongelmaa. Nyt esineillä on kineettinen energia, joka liittyy heidän liikkeeseen. Mitä tuolla energialla voi tapahtua kaatumisen yhteydessä?

Objektien välisen törmäyksen aikana tapahtuvat sisäiset voimat ovat voimakkaita. Kun todetaan, että kineettinen energia ei säilytetä, se tarkoittaa, että se muuttuu muun tyyppisiksi energiaiksi: esimerkiksi äänenergiassa (laitteen törmäyksellä on erottuva ääni).

Lisää käyttömahdollisuuksia kineettiseen energiaan: lämpöä kitkalla ja tietysti väistämättömät muodonmuutokset, joita esineet kärsivät törmääessä, kuten yllä olevassa kuvassa.

[TOC]

Esimerkkejä joustamattomista törmäyksistä 

- Kaksi massaa Plasticine, joka törmää ja kohtaa yhdessä, liikkuen kuin yksi kappale kaatumisen jälkeen.

- Kumipallo, joka pomppii seinää tai lattiaa vasten. Pallo muodonmuutos vaikuttaa pintaan.

Kaikki kineettinen energia ei muuteta muun tyyppisiksi energiaiksi, paitsi muutamia poikkeuksia. Esineet voivat pysyä tietyn määrän tätä energiaa. Myöhemmin näemme kuinka laskea prosenttiosuus.

Kun törmäävät kappaleet ovat yhteydessä toisiinsa, törmäys kutsutaan täydellisesti joustamattomiksi, ja molemmat päätyvät yleensä liikkumaan yhdessä.

Täysin joustamaton törmäys ulottuvuudessa

Kuvion törmäys näyttää kaksi eri massan kohteita m₁ ja m₂, Siirtyminen toisiinsa nopeudella v_I1 ja v_I2 vastaavasti. Kaikki tapahtuu vaakasuunnassa, ts. Se on ulottuvuuden törmäys, yksinkertaisin tutkia.

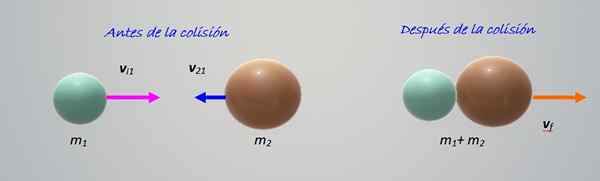Kuva 2. Kahden eri massan hiukkasen törmäys. Lähde: Itse tehty.

Esineet törmäävät ja sitten yhdistyvät oikealle. Se on täysin joustamaton törmäys, joten riittää, että pidämme liikkeen määrän:

P_jompikumpi = P_F

Liikkeen määrä on vektori, jonka yksiköt ovat n.s. Kuvattussa tilanteessa vektorimerkintä voidaan luopua, koska se on ulottuvuuden törmäyksiä:

Se voi palvella sinua: helppoja fysiikan kokeita (ensisijainen yliopisto)

MV_jompikumpi = MV_F

Järjestelmän liikkumisen määrä on kunkin hiukkasen liikkumisen määrän vektorisumma.

m₁ v_I1  + m₂ v_I2 = (m₁ + m₂) v_F

Lopullinen nopeus annetaan:

v_F = (m₁ v_I1  + m₂ v_I2)/ (M₁ + m₂-A

Palautuskerroin

On määrä, joka voi osoittaa kuinka joustava törmäys on. Se on noin palautuskerroin, joka määritellään negatiiviseksi suhteeksi hiukkasten suhteellisen nopeuden välillä kaatumisen jälkeen ja suhteellisen nopeuden ennen onnettomuutta.

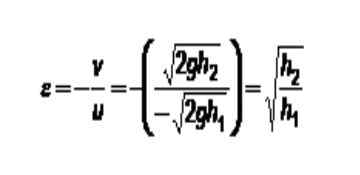
Antaa u₁ ja sinä₂ Hiukkasten vastaavat nopeudet alun perin. Ja ole v₁ ja v₂ vastaavat lopulliset nopeudet. Matemaattisesti palautuskerroin voidaan ilmaista seuraavasti:

Palautuskerroin on lisämäärä, koska se on nopeuden välinen suhde. Mutta toimitetut tiedot ovat erittäin mielenkiintoisia:

- Jos ε = 0 vastaa sen V: n ilmoittamista₂ = v₁. Se tarkoittaa, että lopulliset nopeudet ovat samat ja yhteenotto on joustamaton, kuten edellisessä osassa on kuvattu.

- Kun ε = 1 tarkoittaa, että suhteellinen nopeus sekä ennen onnettomuutta että sen jälkeen eivät muutu, tässä tapauksessa yhteenotto on joustava.

- Ja jos 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Kuinka määrittää palautuskerroin?

Palautuskerroin riippuu törmäyksessä mukana olevista materiaaliluokasta. Erittäin mielenkiintoinen testi sen määrittämiseksi, kuinka elastinen on materiaali pallojen valmistamiseksi, on pudottaa pallo kiinteälle pinnalle ja mitata palautumiskorkeus.

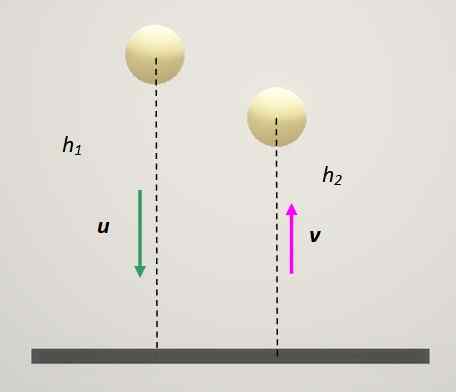Kuva 3. Menetelmä palautuskertoimen määrittämiseksi. Lähde: Itse tehty.

Tässä tapauksessa kiinteällä levyllä on aina nopeus 0. Jos tämä hakemisto 1 on osoitettu tähän ja pallo on: Hakemisto 2 pysyy:

Alkuperäinen nopeus riippuu korkeudesta h₁ josta hän pudotti:

Negatiivinen merkki osoittaa suuntaa. Ja lopullinen nopeus liittyy maksimikorkeuteen h₂ Se ulottuu palautumiseen:

Korvaus palautuskertoimessa:

Räjähdys

Alussa on ehdotettu, että kaikki kineettinen energia voidaan muuttaa siirtymällä muun tyyppisiin energiaan. Loppujen lopuksi energiaa ei tuhota. Onko mahdollista, että liikkeen mukana tulevat esineet törmäävät ja yhdistävät yhteen yhden esineen, joka yhtäkkiä on levossa? Tämä ei ole niin helppoa kuvitella.

Se voi palvella sinua: Dynamiikka: Historia, mitä tutkimuksia, lakeja ja teorioita

Kuvittelemme kuitenkin, mitä tapahtuu taaksepäin, kuten takana olevassa elokuvassa. Sitten objekti oli alun perin lepoa ja räjähtää sitten pirstoutumisen useisiin osiin. Tämä tilanne on täysin mahdollista: se on räjähdys.

Niin, että räjähdys voidaan ajatella täydellisen joustamattomana törmäyksenä, joka on nähty taaksepäin ajassa. Myös liikkeen määrä säilyy, kyky vakuuttaa, että:

P_jompikumpi = P_F

Ratkaistu esimerkki

-Harjoitus 1

Mittauksista tiedetään, että teräksen palautuskerroin on 0.90. Teräspallo pudotetaan 7 m korkeasta kiinteälle levylle. Laskea:

a) kunnes korkeus pomppii.

b) kuinka kauan se kestää ensimmäisen kosketuksen pinnan ja toisen välillä.

Ratkaisu

a) Käytetään yhtälöä, joka on aiemmin päätelty osiossa palautuskertoimen määrittämistä:

Korkeus puhdistuu h₂-

0 -.90² . 7 m = 5.67 m

b) nostaa 5.67 metriä nopeus: Antama:

Mistä:

Ja aika, joka kuluu tämän korkeuden saavuttamiseen, on:

t _Max = v_jompikumpi/ g = (10.54/9.8 s) = 1.08 s.

Palautukseen tarvittava aika on sama, joten 5: n lähettäminen 5.67 metriä ja palaaminen lähtöpisteeseen on kaksinkertainen enimmäisaika:

t_lento = 2.15 s.

-Harjoitus 2

Kuva näyttää massapuunlohkon m, joka roikkuu loput pituus L -langat, heilurina. Tätä kutsutaan ballistiseksi heiluriksi ja se mitataan pääsyn nopeuden v massa massa m. Mitä suurempi nopeus, jolla luoti vaikuttaa lohkoon, korkeammalla korkeudella H tämä rakennetaan.

Kuvaluoti on upotettu lohkoon, joten se on täysin joustamaton isku.

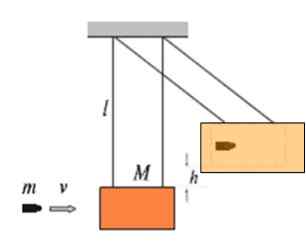Kuva 4. Ballistinen heiluri.

Oletetaan, että 9 9.72 g: n vaikutus massalohkoon 4.60 kg, sitten sarja nousee arvoon 16.8 cm tasapainopaikasta. Mikä on nopeus v luodin?

Ratkaisu

Törmäyksen aikana liikkeen määrä säilytetään ja tai_F Se on sarjan nopeus, kun luoti on upotettu lohkoon:

P_jompikumpi = P_F

Lohko lepää alun perin, kun luoti on suunnattu kohteeseen nopeudella v-

m.v + m.0 = (m + m) u_F

 

Sitä ei tiedetä tai_F Jopa, mutta törmäyksen jälkeen mekaaninen energia säilyy, tämä on gravitaatiopotentiaalienergian ja kineettisen energian summa k:

Voi palvella sinua: Vektorien summa: Graafinen menetelmä, esimerkit, ratkaisut harjoitukset

Alkuperäinen mekaaninen energia = lopullinen mekaaninen energia

JA_MO = E_Mf

TAI_jompikumpi + K -k -_jompikumpi = U_F + K -k -_F

Gravitaatiopotentiaalienergia riippuu korkeudesta, jolla sarja saavuttaa. Tasapainoasennossa alkuperäinen korkeus on vertailuasteena, siksi:

TAI_jompikumpi = 0

Luodin ansiosta sarjassa on kineettinen energia K -k -_jompikumpi, josta tulee gravitaatiopotentiaalienergia, kun sarja saavuttaa suurimman korkeutensa h. Kineettinen energia antaa:

K = ½ mV²

Alun perin kineettinen energia on:

K -k -_jompikumpi = (1/2) (m+m) u_F²

Muista, että luoti ja lohko muodostavat yhden massaobjektin M+ m. Gravitaatiopotentiaalienergia, kun he ovat saavuttaneet suurimmalla korkeudellaan, on:

TAI_F = (m + m) gh

Siksi:

K -k -_jompikumpi = U_F

(1/2) (m+m) u_F² = (m + m) gh

Nyt tämä tulos korvataan ilmaisussa v joka puhdistettiin alussa liikkeen määrän säilyttämisestä:

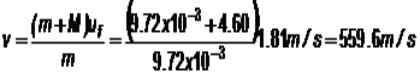
-Harjoitus 3

Kuvion kohde räjähtää kolmessa fragmentissa: kaksi yhtä suuresta massa M ja yksi suurempi massa 2M. Kuva osoittaa kunkin fragmentin nopeuden räjähdyksen jälkeen. Mikä oli objektin alkuperäinen tavoite?

Kuva 5. Kivi, joka räjähtää 3 fragmentissa. Lähde: Itse tehty.

Ratkaisu

Tämä ongelma vaatii kahden koordinaatin käytön: x ja ja, Koska kahdella fragmentilla on pystysuoria nopeuksia, kun taas loput ovat vaakasuoran nopeuden.

Kohteen kokonaismassa on kaikkien fragmenttien massa:

M = M + M + 2M = 4M

Liikkeen määrä säilytetään sekä X -akselilla että Y -akselilla, sitä ehdotetaan erikseen:

1. 4M. tai_x= m v₃
2. 4M. tai_ja = m. 2V₁ - 2M. v₁

Huomaa, että suuri fragmentti liikkuu alas V1 -nopeudella, tämän tosiasian huomauttamiseksi on sijoitettu.

Toisesta yhtälöstä se seuraa heti tai_ja = 0, Ja ensimmäinen on selkeä UX heti:

Objektin alkuperäinen tavoite oli u_jompikumpi = u_x = v₃/4.

Viitteet

1. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fysiikan perusteet. Pearson. 135-155.
3. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Cengage -oppiminen. 172 -182
4. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti. 217-238
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. MacGraw Hill. 185-195