Brayton -sykliprosessi, tehokkuus, sovellukset, harjoitukset

Hän Brayton -sykli Se on termodynaaminen sykli, joka koostuu neljästä prosessista ja koskee puristuvaa termodynaamista nestettä, kuten kaasua. Hänen ensimmäinen mainintansa on peräisin 1800 -luvun lopusta, vaikka hän vietti jonkin aikaa ennen kuin James Joule nosti hänet. Siksi se tunnetaan myös nimellä Joule Cycle.

Se koostuu seuraavista vaiheista, jotka on havainnollistettu sopivasti painekaaviossa - kuvion 1 tilavuus: adiabaattinen puristus (lämpöä ei vaihdeta), isobarinen laajeneminen (tapahtuu vakiopaineessa), adiabaattista laajentumista (lämpöä ei vaihdeta) ja isobarinen puristus (tapahtuu vakiopaineessa).

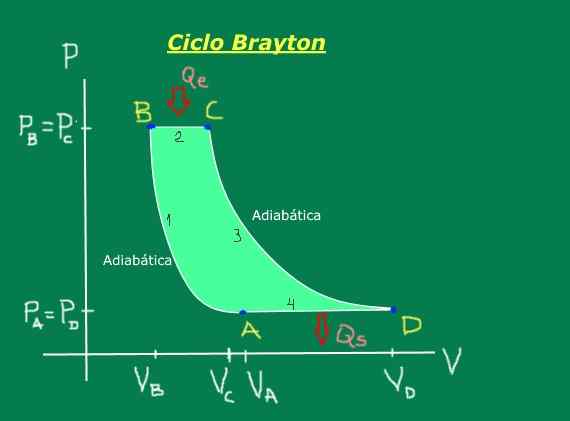Kuvio 1. Brayton -sykli. Lähde: Itse tehty.

[TOC]

Prosessi ja kuvaus

Brayton-sykli on ihanteellinen termodynaaminen sykli, jota käytetään parhaiten kaasuturbiinien termodynaamisen toiminnan selittämiseen ja sekoittaen ilma-polttoainetta, jota käytetään sähkön tuottamiseen ja ilmailumoottoreissa.

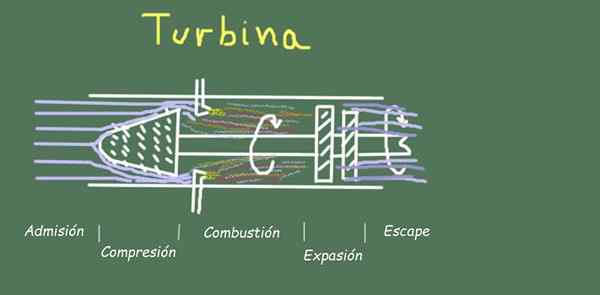Kuva 2. Turbiinijärjestelmä ja virtausvaiheet. Lähde: Itse tehty.

Esimerkiksi turbiinin toiminnassa operaatiokaasun virtauksessa on useita vaiheita, jotka näemme alla.

Pääsy

Se koostuu ilman sisääntulosta lämpötilassa ja ympäristöpaineessa, joka johtuu turbiinin avaamisesta.

Puristus

Ilma puristetaan kehrämällä paletteja toisia vastaan, jotka on kiinnitetty turbiinikompressorin osaan. Tämä pakkaus on niin nopea, että lämmönvaihtoa ei käytännössä ole, joten se on mallinnettu Brayton Cycle AB -prosessin kautta. Kompressorin poistumisilma on nostanut painetta ja lämpötilaa.

Palaminen

Ilma sekoitetaan propaanikaasun tai jauhemaisen polttoaineen kanssa, joka tuo palamiskammion injektorit. Seos tuottaa kemiallisen palamureaktion.

Tämä reaktio tarjoaa lämmön, joka lisää kaasuhiukkasten lämpötilaa ja kineettistä energiaa, jotka laajenevat palamiskammiossa vakiopaineessa. Brayton -syklissä tämä vaihe on mallinnettu BC -prosessilla, joka tapahtuu vakiopaineessa.

Laajennus

Itse turbiinin osassa ilma kasvaa edelleen turbiinipaletteja vastaan, jolloin se pyöri ja tuottaa mekaanista työtä. Tässä vaiheessa ilma alentaa lämpötilaa, mutta vaihtamatta lämpöä käytännöllisesti ympäristön kanssa.

Brayton -syklissä tätä vaihetta simuloidaan adiabaattisen laajennusprosessin CD -levyksi. Osa turbiinin työstä siirretään kompressoriin ja toista käytetään generaattorin tai potkurin siirtämiseen.

Pakokaasu

Lähtevä ilma on vakiopaine, joka on yhtä suuri kuin ympäristö ja tuottaa lämpöä valtavan ulkoisen ilman massan, joten lyhyessä ajassa se vie saman sisääntulon ilman lämpötilan. Brayton -syklissä tätä vaihetta simuloidaan vakiopaineprosessilla, sulkemalla termodynaaminen sykli.

Tehokkuus lämpötilan, lämmön ja paineen perusteella

Ehdotamme Brayton -syklin tehokkuuden laskemista, jolle aloitamme saman määritelmästä.

Lämpökoneessa tehokkuus määritellään koneen, joka on tehty koneen, jaettuna annettuun lämmönergiaan.

Se voi palvella sinua: kevyt heijastus

Termodynamiikan ensimmäinen periaate osoittaa, että termodynaamisen prosessin kaasun nettolämpö on yhtä suuri kuin kaasun sisäisen energian vaihtelu sekä saman tekemän työn vaihtelu.

Mutta täydellisessä syklissä sisäisen energian variaatio on tyhjä, joten se on, että syklissä vaikuttava nettolämpö on yhtä suuri kuin tehdyt nettotyöt.

Saapuva lämpö, ​​lähtevä lämpö ja tehokkuus

Aikaisempi lauseke antaa meille mahdollisuuden kirjoittaa tehokkuutta absorboituneen tai saapuvan lämmön (positvo) ja määritetyn tai lähtevän QS: n (negatiivisen) perusteella (negatiivinen) perusteella.

Lämpö ja paine Brayton -syklissä

Brayton -syklissä lämpö tulee BC -isobariseen prosessiin ja tulee esiin isobarisessa prosessissa.

Olettaen, että vakiopainetta, joka toimitetaan herkällä lämmöllä, että BC -prosessissa sen lämpötila nousee TB: stä TC: hen seuraavan suhteen mukaan:

Missä cp Se on lämpökapasiteetti vakiopaineessa.

Lähtevä lämpö Qs Se voidaan laskea samalla tavalla seuraavalla suhteella, joka koskee prosessia vakiopaineessa: antaa:

Näiden lausekkeiden korvaaminen ilmaisussa, joka antaa meille tehokkuuden saapuvan lämmön ja lähtevän lämmön perusteella, mikä tekee asiaankuuluvista yksinkertaistuksista seuraavaa tehokkuuden suhdetta: saadaan:

Seurauksena, että tehokkuus on riippumaton turbiinin läpi kulkevasta ilmamassasta.

Yksinkertaistettu tulos

Edellistä tulosta on mahdollista yksinkertaistaa, jos otamme sen huomioon PA = PD ja? PB = PC Koska AD- ja BC -prosessit ovat Isobárica, toisin sanoen samassa paineessa.

Lisäksi, koska AB- ja CD -prosessit ovat adiabaattisia, Poissonin suhde molemmille prosesseille toteutetaan:

Missä Gamma edustaa adiabaattista osamäärää, ts. Kuumenenkapasiteetin välinen osoitus vakiopaineessa ja lämpökapasiteetti vakiotilavuudella.

Näiden suhteiden ja ihanteellisen kaasun osavaltion yhtälön suhteen käyttäminen voimme saada vaihtoehtoisen ilmaisun Poissonin suhteeseen:

Kuten tiedämme sen PA = PD ja? PB = PC Jäsenen korvaaminen ja jakaminen jäseneksi saadaan seuraava suhde:

Jos jokainen edellisen yhtälön jäsen vähennetään yksiköstä, ero ratkaistaan ​​ja termit on kiinteä, voidaan osoittaa, että:

Jotta tehokkuus voidaan kirjoittaa ilmanlämpötilan funktiona sisääntulossa ja ilman lämpötilassa puristusprosessin AB lopussa.

Suorituskyky painosuhteesta riippuen

Lämpötiloihin perustuva Brayton -syklin tehokkuudelle saatu ekspressio voidaan kirjoittaa muotoilemaan kompressorin tulosten ja sisäänkäynnin painosuhteen perusteella.

Tämä saavutetaan, jos Poissonin suhteet pisteiden A ja B välillä tunnetaan painosta ja lämpötilasta riippuen, mikä saa syklin tehokkuuden seuraavasti:

Se voi palvella sinua: suhteellinen paine: kaava, miten se lasketaan, esimerkkejä, liikunta

Ramäärä PB: n ja PA: n välillä.

Tyypillinen painisuhde on 8. Tässä tapauksessa Brayton -syklin teoreettinen suorituskyky on 45%.

Sovellukset

Brayton -sykli mallina koskee termosähkölaitoksissa käytettyjä kaasuturbiineja sähköä tuottavien generaattoreiden siirtämiseksi.

Se on myös teoreettinen malli, joka sopii hyvin lentokoneissa käytettyjen turbohenerien moottorien toimintaan, mutta sitä ei voida soveltaa lentokoneiden turboreaktoreilla.

Kun se on kiinnostunut.

Kuva 3. Turbofanimoottori tehokkaampi kuin turboreactor. Lähde: Pixabay

Toisaalta lentokoneiden turboreaktorissa se ei ole kiinnostunut.

Päinvastoin, se on kiinnostunut.

Ratkaisut

-Harjoitus 1

Termosähkölaitoksissa käytettävä kaasuturbiini on paine 800 kPa: n kompressorin poistoaukossa. Saapuvan kaasun lämpötila on ympäristö ja 25 celsius, ja paine on 100 kPa.

Palamiskammiossa lämpötila nousee 1027 celsiukseen päästäkseen turbiiniin.

Määritä syklin tehokkuus, kaasun lämpötila kompressorista ja kaasun lämpötila turbiinin poistossa.

Ratkaisu

Koska meillä on kaasun paine kompressorin ulostulossa ja tiedämme, että syöttöpaine on ilmakehän paine, on mahdollista saada painisuhde:

R = pb / pa = 800 kPa / 100 kPa = 8

Koska kaasu, jolla turbiini toimii.

Tehokkuus lasketaan sitten näin:

Missä olemme soveltaneet suhdetta, joka antaa Brayton -syklin tehokkuuden kompressorin painesuhteesta riippuen.

Lämpötilan laskenta

Kompressorin poistumisen lämpötilan määrittämiseksi tai mikä on sama lämpötila, jolla kaasu tulee palamiskammioon, käytämme suhteen suhdetta kompressorin syöttö- ja poistumislämpötiloihin.

Jos puhdistamme TB -lämpötilan kyseisestä lausekkeesta, saadaan:

Toisin sanoen, pre -combusion -lämpötila on 804,12 celsius.

Harjoituksen harjoittamisena, joka meidän on palamisen jälkeen, lämpötila nousee 1027 celsiukseen, päästäksesi turbiiniin. Osa kaasun lämpöenergiaa käytetään turbiinin siirtämiseen, joten lämpötilan sen poistumisen jälkeen on oltava alhaisempi.

Voi palvella sinua: energian, voiman, voiman, työkonseptien sovellukset

Lämpötilan laskemiseksi turbiinin ulostulossa käytämme aikaisemmin lämpötilan välillä:

Sieltä puhdistamme TD: n saadaksemme lämpötilan turbiinin poistoaukossa. Laskelmien suorittamisen jälkeen lämpötila on:

TD = 143,05 celsius.

-Harjoitus 2

Kaasuturbiini seuraa Brayton -sykliä. Kompressorin lähdön ja sisäänkäynnin välillä on 12.

Oletetaan, että ympäristön lämpötila on 300 K. Lisätietoja tiedetään, että kaasun lämpötila palamisen jälkeen (ennen turbiinin sisäänkäyntiä) on 1000k.

Määritä lämpötila kompressorin ulostulossa ja lämpötila turbiinin poistoaukossa. Määritä myös kuinka monta kiloa kaasua kiertää turbiinin läpi joka sekunti, tietäen, että sen voima on 30 kW.

Oletetaan kaasun erityinen lämpö vakiona ja ota sen arvo huoneenlämpötilassa: CP = 1 0035 J / (kg k).

Oletetaan myös, että kompressorin puristustehokkuus ja turbiinin dekompressio on 100%, mikä on idealisointi, koska käytännössä menetykset tapahtuvat aina.

Ratkaisu

Kompressorin poistumisen lämpötilan määrittämiseksi, tunnettu lämpötila sisäänkäynnissä, meidän on muistettava, että se on adiabaattinen puristus, joten Poissonin suhde AB -prosessiin voidaan soveltaa.

Tällä tavalla saamme, että TB -lämpötila kompressorin ulostulossa on antanut:

Samoin turbiinin ylittävien kaasujen dekompressio on adiabaattinen prosessi, joka vastaa Brayton -sykliprosessia. Siksi voimme soveltaa Poissonin suhdetta turbiinin poistolämpötilan saamiseksi.

Kaikille termodynaamisille syklille nettotyöt ovat aina yhtä suuret kuin syklissä vaihdettu nettolämpö.

Edellisessä suhteessa, joka on saapuva (positiivinen) lämpö ja QS lähtevä (negatiivinen) lämpö. Brayton -syklissä nämä vaihdot tapahtuvat BC- ja DA -prosessit, molemmat Isobáricas.

Nettotyö toimintasyklin kohdalla voidaan sitten ilmaista riippuen kyseisessä jaksossa ja lämpötiloissa kiertävästä kaasun massasta.

Tässä ilmaisussa m Se on kaasun massa, joka kiertää turbiinin läpi toimintajaksossa ja CP Erityinen lämpö.

Jos otamme johdannaisen edellisen ekspression ajan suhteen, saadaan nettoväliaineen massavirtauksen perusteella.

Puhdistus m piste, ja lämpötilojen, kaasun teho- ja lämpökapasiteetin korvaaminen saamme massavirtauksen 1578,4 kg/s.

Viitteet

1. Alfaro, J. Termodynaamiset syklit. Toipunut: fis.Pukki.Cl.
2. Fernández J.F. Brayton -sykli. Kaasuturbiini. TAI.T.N. (Mendoza). Palautettu: Edutecne.Utn.Edu.AR.
3. Sevillan yliopisto. Fysiikan osasto. Brayton -sykli. Toipunut: Laplace.meille.On.
4. Táchiran kansallinen kokeellinen yliopisto. Kuljetusilmiöt. Kaasuvoimyklit. Toipunut: UNET.Edu.mennä.
5. Wikipedia. Brayton -sykli. Toipunut: Wikiwand.com
6. Wikipedia. Kaasuturbiini. Toipunut: Wikiwand.com.