Carnot Cycle -vaiheet, sovellukset, esimerkit, harjoitukset

Hän Karnot -sykli Carnot -moottorissa tapahtuu termodynaamisten prosessien sekvenssi, ihanteellinen laite, joka koostuu vain palautuvista prosesseista; toisin sanoen ne, jotka ovat tapahtuneet, voivat palata alkuperäiseen tilaan.

Tämän tyyppistä moottoria pidetään ihanteellisena, koska siitä puuttuu hajoaminen, kitka tai viskositeetti, joka syntyy todellisissa koneissa, lämpöenergian muuttaminen käyttökelpoiseksi työksi, vaikka muuntamista ei suoriteta 100%.

Kuvio 1. Höyryveturi. Lähde: Pixabay

Moottori on rakennettu perustuen siihen aineeseen, joka pystyy tekemään työtä, kuten kaasua, bensiiniä tai höyryä. Tämä aine kohdistuu erilaisiin lämpötilan muutoksiin ja puolestaan ​​sen paine- ja tilavuuden vaihtelut. Tällä tavalla on mahdollista siirtää mäntä sylinterin sisällä.

[TOC]

Mikä on Carnot -sykli?

Carnot -sykli tapahtuu Carnot- tai C -moottorin nimissä olevassa järjestelmässä, joka on ihanteellinen kaasu, joka on lukittu sylinteriin ja joka on varustettu männän kanssa, joka on kosketuksessa kahteen lähteeseen eri lämpötiloissa T₁ ja T₂ kuten seuraavassa kuvassa esitetty vasemmalla puolella.

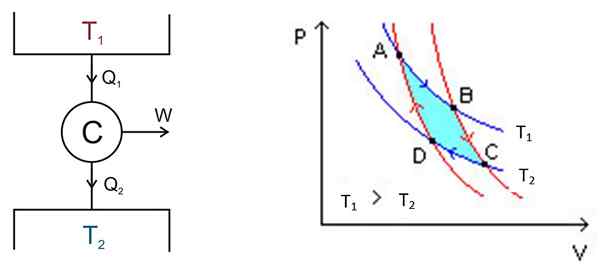Kuva 2. Vasemmalle C Arnot -koneen kaavio, oikealla puolella PV -kaavio. Vasemman kuvan lähde: Keta - oma työ, CC 2: lla.5, https: // commons.Wikimedia.org/w/indeksi.Php?Curid = 681753, oikea kuva Wikimedia Commons.

Karkeassa tilassa on seuraavat prosessit:

1. Laitteeseen toimitetaan tietty määrä lämpöä_{Sisäänkäynti} = Q₁ Lämpösäiliöstä korkeassa lämpötilassa t₁.
2. Carnot C -moottori suorittaa teoksen w tämän toimitetun lämmön ansiosta.
3. Osa käytetystä lämmöstä: jäte Q_poistuminen, Se siirretään lämpösäiliöön, joka on alhaisemmassa lämpötilassa t₂.

Carnot Cycle -vaiheet

Analyysi tehdään p -V -kaaviolla (painekolme), kuten kuvassa 2 esitetään (oikea kuva). Moottorin tavoitteena voi olla pitää lämpövarasto 2 kylmänä, purkamalla siitä lämpöä. Tässä tapauksessa se on a Jäähdytyskone. Jos päinvastoin, haluat antaa lämpöä lämpövaraston 1, niin se on a Lämpöpumppu.

P -V -kaavio näyttää paineen muutokset - moottorin lämpötila kahdessa olosuhteessa:

- Vakiolämpötilan ylläpitäminen (isoterminen prosessi).

- Ei lämmönsiirtoa (lämpöeristys).

Kaksi isotermistä prosessia on kytkettävä, mikä saavutetaan lämpöeristyksen avulla.

Kohta

Voit aloittaa missä tahansa syklin vaiheessa, jossa kaasulla on tietty paine-, tilavuus- ja lämpötilaolosuhteet. Kaasu kärsii prosessisarjasta ja voi palata aloitusolosuhteisiin uuden syklin aloittamiseksi, ja aina lopullinen sisäinen energia on sama kuin alku. Koska energia säilyy:

Työskentely C = syöttölämpö - lähtölämpö

ΔW = Q_{Sisäänkäynti} - Q -_poistuminen

Tähän sykliin tai silmukkaan sisältyvä alue, joka on kuvan turkoosi, on tarkkaan Carnot -moottorin tekemä työ.

Pisteet A, B, C ja D on merkitty kuvassa 2. Se alkaa pisteestä, joka seuraa sinistä nuolta.

Ensimmäinen vaihe: isoterminen laajennus

Pisteiden A ja B välinen lämpötila on t₁. Järjestelmä imee lämpöä lämpövaraston 1 ja kärsii isotermisen laajentumisen. Sitten tilavuus kasvaa ja paine laskee.

Lämpötila pysyy kuitenkin T: ssä₁, Siitä lähtien, kun kaasu laajenee, se jäähtyy. Siksi sen sisäinen energia pysyy vakiona.

Se voi palvella sinua: Graff Van Generaattori: Juhlat, miten se toimii, sovellukset

Toinen vaihe: Adiabaattinen laajennus

Kohdassa B järjestelmä aloittaa uuden laajennuksen, jossa järjestelmä ei voita tai menetä lämpöä. Tämä saavutetaan asettamalla se kalorieristykseen, kuten aiemmin on osoitettu. Siksi se on adiabaattinen laajennus, joka jatkaa pistettä C punaisen nuolen jälkeen. Tilavuus kasvaa ja paine laskee, kunnes se saavuttaa alimman arvonsa.

Kolmas vaihe: isoterminen puristus

Aloita kohdasta C ja lopu d. Eristys poistetaan ja järjestelmä joutuu kosketuksiin lämpövaraston 2 kanssa, jonka lämpötila t₂ Se on vähemmän. Järjestelmä tuottaa jätesäiliöön lämmön säiliöön, paine alkaa kasvaa ja tilavuus vähenee.

Neljäs vaihe: Adiabaattinen puristus

Pointiin D saavutettu järjestelmä palaa takaisin lämpöeristykseen, paine nousee ja tilavuus pienenee, kunnes se on kohdan A alkuperäiset olosuhteet saavuttaa. Sitten sykli toistetaan uudelleen.

Carnotin lause

Carnotin lause postuloi ensimmäisen kerran 1800 -luvun alussa ranskalainen fyysikko Sadi Carnot. Vuonna 1824 Carnot, joka oli osa Ranskan armeijaa, julkaisi kirjan, jossa hän ehdotti vastausta seuraavaan kysymykseen: Missä olosuhteissa lämpökoneella on maksimaalinen tehokkuus? Sitten Carnot perusti seuraavan:

Mikään lämpömoottori, joka kulkee kahden lämpökerroksen välillä, ei ole tehokkaampaa kuin Carnot -moottori.

Lämpömoottorin η -sato annetaan W: n ja absorboituneen lämmön välisellä suhteella Q:

Suorituskyky = tehty työ/lämpö imeytynyt

Tällä tavalla minkä tahansa lämpömoottorin I suorituskyky on: η = w/q. Vaikka Carnot R -moottorin suorituskyky on η = w/q ', molempien moottorien tapauksessa he pystyvät suorittamaan saman työn.

Carnotin lause toteaa, että η ei ole koskaan suurempi kuin η '. Muuten se kuuluu termodynamiikan toisen lain kanssa, jonka mukaan prosessi, jonka seurauksena on, että lämmöä alhaisemman lämpötilan rungosta on mahdotonta siirtyä toiseen korkeampaan lämpötilaan saamatta ulkoista apua. Siksi:

η _< η^'

Carnotin lauseen esittely

Osoittaa, että näin on, harkitse Carnot -moottoria, joka toimii jääkaappikoneeksi, jota ajaa I -moottori. Tämä on mahdollista, koska Carnot -moottori toimii palautuvien prosessien avulla, kuten alussa määritetään.

Kuva 3. Carnotin lauseen esittely. Lähde: Netheril96 [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Sinulla on molemmat: minä ja r työskentelen samoilla lämpökerrostumilla ja oletetaan, että η _- η^'. Jos matkan varrella on ristiriita termodynamiikan toisella laki, Carnotin lause osoitetaan vähentämällä absurdillisuutta.

Kuva 3 auttaa seuraamaan prosessia. I -moottori ottaa määrän lämpöä Q, joka jakaa tällä tavalla: Tehtävä R -vastaava W = ηq ja loput on siirretty lämpö (1 -η) q lämpösäiliöön T₂.

Koska energia säilyy, kaikki toteutetaan:

JA_{Sisäänkäynti} = Q = työ W + T: lle määritetty lämpö₂ = ηq + (1 -η) q = e_poistuminen

Nyt Carnot R -jääkaappikone ottaa lämpösäiliön 2, jonka lämmö on antanut:

Se voi palvella sinua: IMANTANTION: Mikä koostuu, menetelmä ja esimerkit

(η / η ') (1 -η') Q =

Energiaa on myös pidettävä tässä tapauksessa:

JA_{Sisäänkäynti} = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_poistuminen

Tuloksena on siirto lämpösäiliöön t₂ (η / η ') Q = Q'.

Jos η on suurempi kuin η ', se tarkoittaa, että korkein lämpötilan lämpövarasto on saapunut enemmän lämpöä kuin alun perin otin. Koska yksikään ulkoinen agentti, kuten toinen lämpölähde, ei ole osallistunut, ainoa tapa, jolla se voi tapahtua, on, että kylmin lämpövarasto tuottaa lämpöä.

Tämä on eri mieltä termodynamiikan toisen lain kanssa. Silloin päättyy, että ei ole mahdollista, että η^' Olla pienempi kuin η, siksi I -moottorilla ei voi olla enemmän suorituskykyä kuin Carnot R -koneella.

Lause ja rajoitukset

Carnot Lause -sovellus toteaa, että kahdella Carnot -koneella on sama tehokkuus, jos molemmat toimivat samoilla lämpökerroksilla.

Tämä tarkoittaa, että aineella ei ole merkitystä, suorituskyky on itsenäinen eikä sitä voida nostaa muuttamalla sitä.

Edellisen analyysin päätelmä on, että Carnot -sykli on ihannetapauksessa saavutettavan termodynaamisen prosessin yläosa. Käytännössä on monia tekijöitä, jotka vähentävät tehokkuutta, esimerkiksi tosiasia, että eristäminen ei ole koskaan täydellistä ja adiabaattisissa vaiheissa on todella kalorien vaihto ulkopinnan kanssa.

Auton tapauksessa moottorilohko lämmitetään. Toisaalta kaasu- ja ilmaseos ei käyttäytyy tarkalleen ihanteellisena kaasuna, joka on Carnot -syklin lähtökohta. Tämä mainitsee vain joitain tekijöitä, jotka aiheuttavat dramaattisen suorituskyvyn vähentämisen.

Esimerkit

Mäntä sylinterin sisällä

Jos järjestelmä on mäntä, joka on lukittu sylinteriin kuten kuvassa 4, mäntä nousee isotermisen laajentumisen aikana, kuten voidaan nähdä äärimmäisen vasemmiston ensimmäisessä kaaviossa ja nousee myös adiabaattisen laajennuksen aikana.

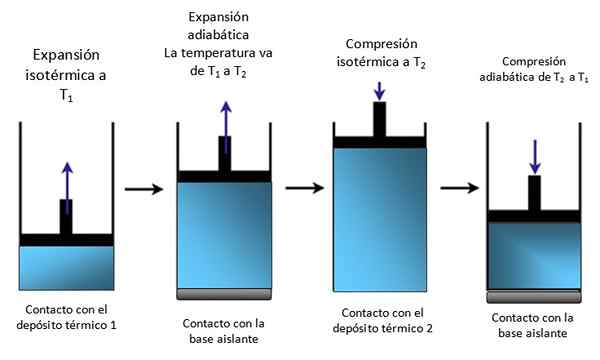Kuva 4. Männän liikkuminen sylinterin sisällä. Lähde: Itse tehty.

Sitten isotermisesti pakattu, antaen lämpöä ja jatkuu edelleen adiabaattisesti. Tuloksena on liike, jossa mäntä nousee ja alas sylinterin sisällä ja voidaan siirtää tietyn laitteen muihin osiin, kuten esimerkiksi automoottori, joka tuottaa parin tai höyryisen koneen.

Erilaisia ​​palautuvia prosesseja

Ihanteellisen kaasun laajennuksen ja puristuksen lisäksi sylinterin sisällä on myös muita ihanteellisia palautuvia prosesseja, joiden kanssa carnot -sykli voidaan konfiguroida, esimerkiksi:

- Edestakaisen matkan liikkeet kitkan puuttuessa.

- Ihanteellinen jousi, joka on pakattu ja puristettu ja joka ei ole koskaan muodonmuutos.

- Sähköpiirit, joissa ei ole resistanssia, joka hajottaisi energiaa.

- Magnetointi- ja demagnetointisyklit, joissa häviämistä ei ole.

- Akun lataaminen ja lataaminen.

Ydinvoimalaitos

Vaikka se on erittäin monimutkainen järjestelmä, seuraava lähestymistapa ydinreaktorin energian tuottamiseksi on seuraavaa:

- Lämpölähde, joka koostuu materiaalista, joka hajoaa radioaktiivisesti kuten uraani.

Voi palvella sinua: Nykyinen atomimalli

- Allas tai kylmä lämpövarasto, joka olisi ilmapiiri.

- "Carnot Machine", joka käyttää nestettä, melkein aina juoksevaa vettä, joka toimitetaan lämpölähteestä lämmön muuttamiseksi höyryksi.

Kun sykli suoritetaan, sähkö saadaan nettotyönä. Kun muutetaan korkean lämpötilan höyryksi, vesi saavutetaan turbiiniin, missä energia muuttuu liikkeeksi tai kineettiseksi energiaksi.

Turbiini puolestaan ​​aktivoi sähkögeneraattorin, joka muuttaa sen liikkeen energian sähköksi. Fosening -materiaalin, kuten uraanin, lisäksi fossiilisia polttoaineita voidaan käyttää lämmönlähteenä.

Ratkaisut

-Esimerkki 1: Lämpökoneen tehokkuus

Lämpökoneen tehokkuus määritellään tulostyön ja sisäänkäynnin väliseksi suhteeksi, ja siksi se on mitoiton määrä:

Suurin hyötysuhde = (Q_{Sisäänkäynti} - Q - _poistuminen) /Q_{Sisäänkäynti}

Merkitsee maksimaalista tehokkuutta E_max, On mahdollista osoittaa sen lämpötilariippuvuus, mikä on helpoin muuttuja mitattavaksi, kuten:

ja_max = 1 - (t₂/T₁-A

Missä t₂ Se on pesuallas ja t₁ Se on lämpölähteen lämpötila. Koska jälkimmäinen on suurempi, tehokkuus osoittautuu aina olevan alle 1.

Oletetaan, että lämpökone pystyy työskentelemään seuraavilla tavoilla: a) välillä 200 K - 400 K, B) välillä 600 K - 400 K. Mikä on joka tapauksessa tehokkuus?

Ratkaisu

a) Ensimmäisessä tapauksessa tehokkuus on:

ja_Max1 = 1 - (200/400) = 0.viisikymmentä

b) Toisella moodilla tehokkuus on:

ja_Max2 = 1- (400/600) = 0.33

Vaikka lämpötilaero on sama molempien moodien välillä, tehokkuus ei ole. Ja vieläkin huomattavampaa on, että tehokkain tila toimii alemmassa lämpötilassa.

-Esimerkki 2: Absorboitunut lämpö ja luovutettu lämpö

22 %: n lämpökone tuottaa 1530 J: n työtä. Löydä: a) lämpövarastoista absorboituneen lämpöä 1, b) lämpösäiliöön hylätyn lämmön määrä 2.

a) Tässä tapauksessa käytetään tehokkuuden määritelmää, koska tehty työ, ei lämpökerrostumien lämpötiloista, ei ole saatavana. 22%: n tehokkuus tarkoittaa, että E _Max = 0.Siksi: siksi:

Suurin hyötysuhde = työ /Q_{Sisäänkäynti}

Absorboituneen lämmön määrä on tarkalleen Q -_{Sisäänkäynti}, Joten puhdistat:

Q -_{Sisäänkäynti} = Työ/tehokkuus = 1530 J/0.22 = 6954.5 J

b) kylmimmalle säiliölle osoitetun lämmön määrä on δ: stäW = q_{Sisäänkäynti} - Q -_poistuminen

Q -_poistuminen = Q_{Sisäänkäynti} - ΔW = 6954.5 -1530 J = 5424.5 J.

Toinen tapa on ja_max = 1 - (t₂/T₁-A. Koska lämpötiloja ei tunneta, mutta nämä liittyvät lämpöä, tehokkuus voidaan myös ilmaista seuraavasti:

ja_max = 1 - (Q_Kiinnitys/Q_imeytynyt-A

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 654-657
2. Ydinenergia. Ydinvoimalaitoksen toiminta. Toipunut: Energian ydin.netto
3. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen. 618-622.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. MacGraw Hill. 414-416.
5. Walker, J.2008. Fysiikka. 4. ed.Addison Wesley. 610-630