Kutsutaan Merkittäviä lukuja numeroiden määrään, joka sisältää Mantisa lukumäärä. Mitä enemmän numeroita määrä tunnetaan suurimmalla tarkkuudella. Muistutuksena, Mantisa on luku, joka seuraa 10: n voimaa, kun tieteellisen merkinnän lukumäärä on kirjoitettu.

Otetaan esimerkiksi numero 0.00376, joka on kirjoitettu 3.76 x 10 ^-3. Mantisa on 3.76 ja lukumäärällä on yhteensä 3 merkittävää lukua. Numero 0.129: llä on myös 3 merkittävää lukua, kun taas 4.5: llä on vain 2.

Kuvio 1. Tieteelliset laskimet eivät koskaan osoita operaation merkittävien lukumääriä. Lähde: Piqsels.

Ja mitä tapahtuu, kun numero on kokonainen? Se tarkoittaa, että se tunnetaan kaikella mahdollisella tarkkuudella, toisin sanoen sillä on ääretön tarkkuus. Esimerkiksi laskemalla ihmisiä, eläimiä tai esineitä, kuten kirjoja ja puhelimia, tulos on kokonaisluku ja tarkka luku.

Jos sanomme, että elokuvateatterissa on 110 ihmistä, jotka katsovat elokuvaa, tämä on tarkka luku, ei enempää eikä vähemmän, ja siinä on 3 merkittävää hahmoa.

Merkittäviä lukuja käsitellään joitain yksinkertaisia ​​sääntöjä, jotka muistetaan pienellä harjoituksella, kuten näemme silloin.

[TOC]

Säännöt lukumäärän merkittävien lukujen määrittämiseksi

Sääntö 1

Edellisiä nollia ei lasketa merkittäväksi lukuksi, joten 0.045 ja 4.5 Heillä on molemmat 2 merkittävää lukua, koska ne alkavat laskea vasemmalta ja alkaen ensimmäisestä nollan numerosta.

Sääntö 2

Takaosan nollat ​​(oikealla) ensimmäiseen merkittävään numeroon lasketaan merkittäväksi lukuksi (niin kauan kuin se on perusteltu mittauslaitteen tarkkuuden avulla).

Lopuksi keskellä olevat nollat ​​lasketaan myös merkittäväksi numeroksi.

Sääntö 3

Tieteellisessä merkinnässä kirjoitettujen lukujen osalta kaikki Mantisa -luvut ovat merkittäviä, ja eksponentti ei vaikuta tarkkuuteen.

Se voi palvella sinua: keskimääräinen nopeus: kaavat, miten se lasketaan ja ratkaistaan

Sääntö 4

Kun desimaalien operaatioita tehdään, esimerkiksi laskemalla alueet tai muut vastaavat toiminnot, tuloksella on oltava sama määrä merkittäviä lukuja kuin määrällä, jolla on alhaisin merkittäviä lukuja, jotka osallistuivat toimintaan. Tämä sääntö on voimassa kaikissa aritmeettisissa operaatioissa.

Sääntö 5

Lukumäärän lukumäärä ei vaikuta sen merkittävien lukujen lukumäärään.

Näemme heti joitain esimerkkejä tästä ja kaikista muista säännöistä.

Esimerkit

Esimerkki 1

Selvitä, kuinka monta merkittävää lukua on jokaisessa näistä numeroista.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Vastaukset

a) 876: lla on 3 merkittävää lukua.

b) 1000.68: lla on 6 merkittävää lukua, koska nollat ​​keskilaskissa sellainen.

c) sen sijaan 0.00005026: lla on 4 merkittävää lukua. Huomaa, että 5: n 5: n vasemmalla puolella olevaa nollaa ei lasketa merkittäväksi lukuksi, sen sijaan 0: n välillä 5 - 2 kyllä.

d) 4.8: lla on 2 merkittävää lukua.

e) -6.99: llä on 3 merkittävää lukua.

Esimerkki 2

On yleistä toteuttaa mittauksia, kuten metrisiä nauhoja, kelloja, lämpömittareita, asteikoita ja niin tyyliä. Kuinka monta merkittävää lukua meidän pitäisi ilmoittaa määrät, jotka mitataan tällä tavalla?

Vastaus

Se riippuu sen instrumentin arvioinnista. Annetaan esimerkki: mittaa putken ulkoinen halkaisija, asteittaisella sääntöllä ja Vernier- tai King's Foot -sovelluksella.

Vernier on instrumentti, joka mittaa pituutta erittäin tarkasti siksi, että sillä on ylimääräinen pieni mittakaava, nimeltään vernier, mikä mahdollistaa niin sanotun hienoa, mitattaessa.

Se on tarkempi kuin asteittainen sääntö, koska sen avulla voimme oppia merkittäviä tietyn pituisia lukuja.

Siksi ei ole mitään järkeä ilmoittaa, esimerkiksi 35.88 cm, jos mitataan sen mittanauhalla, koska tämä instrumentti ei ole tarpeeksi tarkka ilmoittaakseen niin monia merkittäviä numeroita.

Voi palvella sinua: staattinen: historia, mitä tutkimuksia, sovelluksia, lakeja

Tapan mittaus on antanut:

Mittanauhan tai millimetrin sääntö, a = 1 mm, joka on senttimetrin kymmenesosa. Mittanauhalla mitattu kehä on ilmoitettava 35.9 cm.

Esimerkki 3

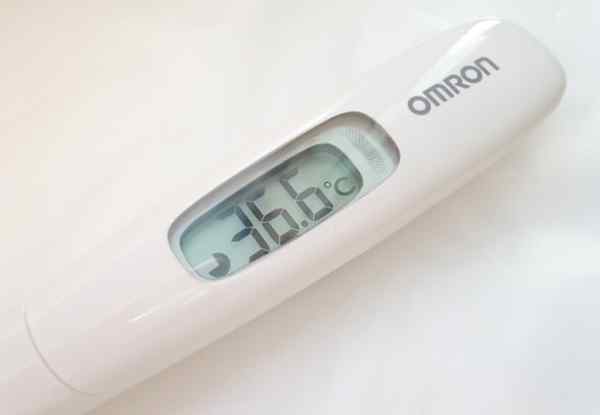
Kuinka monta merkittävää lukua digitaalisella lämpömittarilla on lukema?

Vastaus

Kuvan lämpömittari tarjoaa lämpötilalukemat kolmella numerolla. Kuitenkin osoitetussa määrin, 36.6 ºC, vain kaksi ensimmäistä numeroa vasemmalta oikealle ovat tarkkoja, koska desimaaliin vaikuttaa instrumentin arvostusvirhe, joka on yleensä merkitty saman tai sen operaation käsikirjassa.

Esitetyn digitaalisen instrumentin tyypin tavallinen asia on 0 arvostuksen virhe.1 ºC. Tämä riittää varmistaakseen, ettei kuumetta ole.

Kuva 2. Digitaalinen lämpömittari, jonka lukemat ovat 3 merkittävää lukua. Lähde: Pxhere.

Säännöt pyöreään numeroihin

Kun laskuria käytetään laskelmien suorittamiseen saatujen mittausten avulla, ei ole oikein antaa tulos käyttämällä kaikkia näytöllä näkyviä numeroita.

Vain ne, jotka tuntevat toisensa tarkasti, säilyvät, koska vain niillä on todellinen merkitys. Sitten on tarpeen pyöristää tulokset sopimaan tarkasti tunnetuiden lukujen lukumäärään. Nämä säännöt ovat:

-Jos pidätettävään numeroa seuraavan numero on yhtä suuri tai suurempi kuin 5, Tähän numeroon lisätään 1.

Esimerkiksi pyöristämällä 3.786 Kahden desimaalin saamiseksi haluamme säilyttää luvut 8: een. Koska seuraava luku (6) on suurempi kuin 5, 8: sta tulee 8 + 1 = 9 ja luku pysyy 3.79.

-Kun säilytettävän numeron seuraava numero on Alle 5, Numero on sama.

Voi palvella sinua: Joule -vaikutus: Selitys, esimerkit, harjoitukset, sovellukset

Jos haluamme kiertää 1.27924 vain 3 desimaalista, tämä saavutetaan saavuttamalla 9, jota seuraa 2. Koska 2 on alle 5, nämä desimaalit katoavat ja pyöristetty luku on 1.279.

Liikuntaa

Ruokapöydällä on muoto ja mitat ilmoitettu kiinnitettyyn kuvaan. Sen pinta -alaa pyydetään laskemaan merkittävien lukujen operaatiosääntöjen avulla.

Ratkaisu

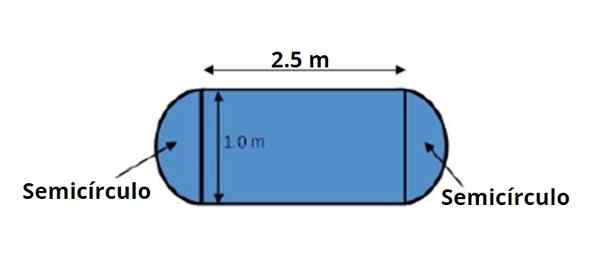Kuva 3. Taulukossa on kuva ja mitat ilmoitettu kuvassa, huomaa, että nämä tunnetaan kahdella merkitsevällä lukulla. Lähde: f. Zapata.

Pöytäalue voidaan jakaa keskimmäiseen suorakulmaiseen alueeseen ja kahteen puolipyöreeseen, joista toinen puolella, jotka yhdessä tekevät yhden täyden ympyrän.

Soitamme₁ Suorakulmion alueelle, antanut:

-Lla₁ = pohja × korkeus = 2.5 m x 1.0 m = 2.5m²

Omastaan ​​ympyräalue, joka vastaa 1 puolipyörän kerrottuna 2: lla, on:

-Lla₂ = π × radio²

Minkä tahansa puolipyörän halkaisija on 1.0 m, siksi säde on 0.50 m. Halkaisijaa voidaan käyttää myös suoraan alueen laskemiseen, tässä tapauksessa:

-Lla₂ = (π × halkaisija²) / 4

Joka tapauksessa:

-Lla₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Kaikki laskimen tarjoamat numerot käytettiin. Nyt lisäämme₁ jo₂ Taulukon kokonaispinta -ala:

A = (2.5 + 0.785398163) m² = 3.285398163 m²

Koska taulukon mitat tunnetaan kahdella merkitsevällä lukulla, ei ole mitään järkeä ilmaista tulosta kaikilla laskimen antamilla desimaaleilla, mikä ei koskaan anna tuloksen merkittävien lukujen lukumäärää.

Alueen ympäri on tehtävä siten, että sillä on sama määrä merkittäviä lukuja kuin taulukon mitat, ts. 2. Siksi lopputulos on ilmoitettu näin:

A = 3.3 m²

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
3. Fiscalab. Merkittävät luvut ja pyöristäminen. Toipunut: fisikab.com.
4. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.