Fyysinen

Vaihtovirtapiirien tyypit, sovellukset, esimerkit

Vaihtovirtapiirien tyypit, sovellukset, esimerkit

Se Vaihtovirtapiirit jompikumpi CA -piirit Ne koostuvat resistiivisten, induktiivisten ja kapasitiivisten elementtien yhdistelmistä yhdistettynä vaihtoehtoisen jännitteen lähteen kanssa, joka on yleensä sinimuotoinen.

Jännitteen levittämisessä muuttuvan virran määritetään lyhyen ajan, nimeltään siirtymävirta, joka antaa tien sinimuotoiselle paikallaan olevalle virralle.

Vaihtovirtapiiri

Sinusoidisella virralla on arvoja, jotka vuorottelevat positiivisen ja negatiivisen välillä, muuttuvat säännöllisiksi väliajoiksi, jotka määritetään aiemmin vakiintuneella taajuudella. Virran muoto ilmaistaan ​​seuraavasti:

I (t) = im Sen (ωt --φ)

Missä minäm Se on virran maksimivirta tai amplitudi, ω on taajuus, t On aika ja φ vaihe -ero. Virtaan yleisesti käytetyt yksiköt ovat vahvistimet (a) ja sen alamulaatiot, kuten Milliamerium ja mikroamperium.

Aika mitataan puolestaan ​​sekunneissa, sillä taajuudella on Hertzios tai Hertz, lyhennetty Hz, kun taas vaiheero on kulma, joka yleensä mitataan radiaaneissa, vaikka joskus sitä esiintyy joskus asteissa. Näitä tai radiaaneja ei pidetä yksiköinä.

Symboli, jota käytetään vaihtoehtoiseen jännitelähteeseen

Usein vaihtoehtoista jännitettä symboloidaan ympyrän sisällä olevalla aaltolla, jotta se erotetaan suorasta jännitteestä, jota symboloivat kaksi epätasa -arvoista ja yhdensuuntaista viivaa.

[TOC]

Tyypit vaihtavat virran piirejä

Vaihtovirtapiirejä on monenlaisia, alkaen seuraavassa kuvassa esitetyistä yksinkertaisimmista piireistä. Vasemmalta oikealle heillä on:

-Kunnioitus vastus r: n kanssa

-Piiri kelalla l

-Piiri kondensaattorilla C.

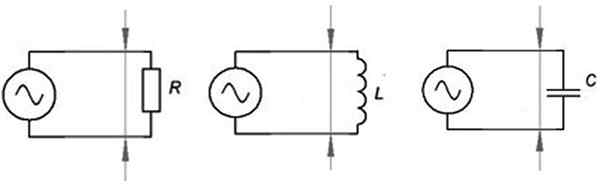Vasemmalta oikealle: resistiivinen, induktiivinen ja lopullinen kapasiteettipiiri. Lähde: f. Zapata.

Piiri resistiivisen elementin kanssa

Piirissä, jonka vastus r on kytketty vaihtoehtoiseen jännitteen lähteeseen, vastusjännite on VR - = Vm Sent. Ohmin laki, joka pätee myös vuorotellen puhtaasti resistiivisiin piireihin:

VR - = IR -∙ r

Siksi enimmäisvirta im = Vm /R.

Sekä virta että jännite ovat vaiheessa, mikä tarkoittaa, että ne saavuttavat maksimiarvot, samoin kuin 0, samanaikaisesti.

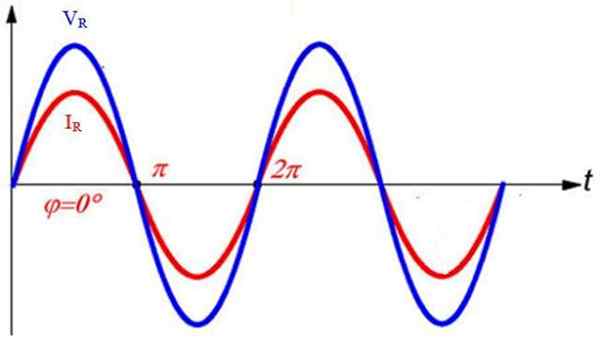Puhtaasti resistiivisessä vuorottelevassa virtapiirissä virta ja vastus ovat vaiheessa. Lähde: f. Zapata.

Induktiivinen elementtipiiri

Kelmissä jännite on VLens = Vm Sen ωt ja liittyy induktorin virtaan yhtälön kautta:

Integroituminen:

Trigonometristen syiden ominaisuuksista ILens Se on kirjoitettu sin ωt: n suhteen:

YllyttääLens = Im sin (ωt - ½ π)

Voi palvella sinua: luonnolliset satelliitit

Sitten jännite ja virta ovat vanhentuneita, jälkimmäinen viivästyi ½ π = 90º jännitteen suhteen (virta alkaa ennen, että lähtökohta on t = 0 s). Tämä nähdään seuraavassa kuvassa verrattuna i: n sinimuotoiseenLens ja V: nLens-

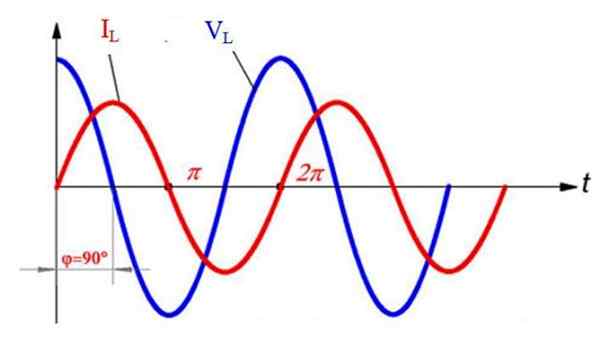Vaihtoehtoinen jännite ja virta puhtaasti induktiivisessa vaihtovirtapiirissä. Lähde: f. Zapata.

Induktiivinen reaktanssi

Induktiivinen reaktanssi määritellään x: ksiLens = Ωl, kasvaa usein ja sillä on vastusmitat, siksi analogisesti Ohmin lain kanssa:

VLens = ILens ∙ xLens

Piiri kapasitiivinen elementti

Conser C: lle, joka on kytketty vuorottelevaan virran lähteeseen, on täytettävä, että:

Q = c ∙ vC = C ∙ vm Sent

Lauhduttimen virta johtaa kuormaan ajan suhteen:

YllyttääC= ωc ∙ Vm cos ωt

Mutta cos ωt = sin (ωt + ½ π), sitten:

YllyttääC = Ωcvm sin (ωt+ ½ π)

Tässä tapauksessa virta etenee jännitteeseen ½ π: ssä, kuten graafisesta voidaan nähdä.

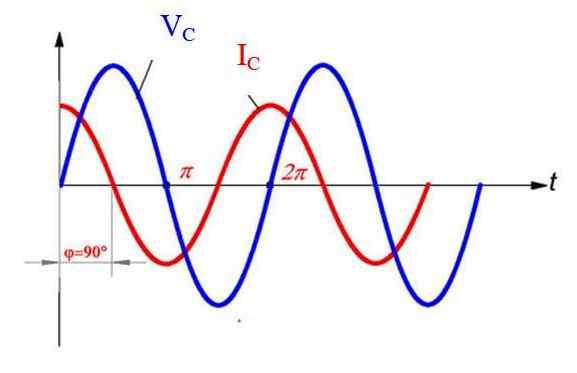Jännite ja virta vaihtoehtoisessa piirissä puhtaasti kapasitiivinen elementti. Lähde: f. Zapata.

Kapasitiivinen reaktanssi

Kapasitiivinen reaktanssi voidaan kirjoittaa xC = 1/ωc, vähenee taajuuden kanssa ja sillä on myös vastusyksiköt, ts. Ohmit. Tällä tavoin Ohmin laki on näin:

VC = XC.YllyttääC

Sovellukset

Michael Faraday (1791-1867) oli ensimmäinen, joka sai virran, joka muutti säännöllisesti sen merkitystä induktiokokeidensa avulla, vaikka alkuaikoina käytettiin vain suoravirtaa.

1800 -luvun lopulla tapahtui hyvin tunnettu virtauksen sota, Thomasin välillä. Edison, Direct Virran käytön puolustaja ja vaihtovirran kannattaja George Westinghouse. Lopuksi tämä voitti talouden, tehokkuuden ja leviämisen helppouden pienillä tappioilla.

Tästä syystä tähän päivään mennessä koteihin ja teollisuuteen liittyvä virta on vuorotellen nykyinen, vaikka tasavirran käyttö ei koskaan kadonnut kokonaan.

Vaihtovirtaa käytetään melkein kaikessa, ja monissa sovelluksissa vuorottelevan virran jatkuva muutos ei ole merkityksellinen, kuten hehkulamput, rauta tai keittäminen torvi, koska resistiivisen elementin kuumentaminen ei riipu siitä kuormien liikkumisen suunta.

Toisaalta se, että virta muuttaa merkitystä tietyllä taajuudella, on sähkömoottorien ja monien tarkempien sovellusten perusta, kuten seuraavat:

Se voi palvella sinua: äänen eteneminen

Pelfming -piirit

Piirit, jotka koostuvat vastuskyvyn ja sarjamakdensaan liittyvästä vaihtoehtoisesta lähteestä, tunnetaan nimellä RC -sarjapiirit, ja niitä käytetään ei -toivottujen lasien poistamiseen toisessa piirissä tai lisäävät myös joitain erikoistehosteita tähän.

Ne toimivat myös jännitteenjakoina ja virittämään radioasemia (katso esimerkki 1 seuraavassa osassa).

Siltatyyppiset piirit

Vaihtovirtaa ruokittuja siltapiirejä voidaan käyttää kapasiteetin tai induktanssin mittaamiseen samalla tavalla kuin Wheatstone -siltaa, hyvin tunnettu suoravirtapiiri, joka pystyy mittaamaan tuntemattoman vastusarvoa.

Esimerkkejä vaihtovirtapiiristä

Edellisissä osioissa kuvailtiin yksinkertaisimmat vuorotellen virran piirit, vaikka tietysti yllä kuvatut peruselementit sekä muut hieman monimutkaisempia, koska diodeja, vahvistimia ja transistoreita voidaan yhdistää muutamia, jotta saadaan erilaisia ​​tehosteita.

Esimerkki 1: RLC -piiri

Yksi yleisimmistä piireistä Ac Se sisältää vastus r, kelan tai induktorin L ja kondensaattorin tai lauhduttimen C -sarjan, jossa on vaihtovirtalähde.

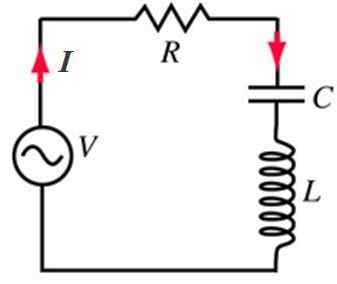RLC -piiri sarjassa, joka ruokitaan vuorottelevalla virran lähteella. Lähde: f. Zapata.

RLC -sarjan piirit reagoivat erityisesti sen vaihtoehtoisen lähteen taajuuteen. Siksi yksi mielenkiintoisimmista sovelluksista on kuin radion viritetyt piirit.

Radiosignaali tuottaa usein virran, jolla on sama taajuus piirissä, joka on erityisesti suunniteltu toimimaan vastaanottimena, ja tämän virran amplitudi on maksimi, jos vastaanotin on viritetty tällä taajuudella, nimeltään tehostetun vaikutuksen kautta resonanssi.

Vastaanottava piiri toimii virittimenä, koska se on suunniteltu siten, että ei -toivottujen taajuuksien signaalit tuottavat hyvin pieniä virtauksia, joita radiokaiuttimet eivät havaitse, ja siksi niitä ei ole kuultava. Toisaalta resonanssitaajuuteen virran amplitudi saavuttaa maksimin ja sitten signaali kuuluu selvästi.

Resonanssitaajuus tapahtuu, kun piirin induktiiviset ja kapasitiiviset reaktanssit tasoitetaan:

XLens = XC

1/ωc = ωl

Ω2 = 1/LC

Radioaseman, jolla on taajuussignaali ω.

Se voi palvella sinua: Normaali työ: mistä se koostuu, miten se lasketaan, esimerkkejä

Esimerkki 2: RLC -piiri rinnakkain

RLC -piireissä rinnakkain on myös tiettyjä vasteita lähdetaajuuden mukaan, mikä riippuu kunkin elementin reaktanssista, määriteltynä jännitteen ja virran väliseksi syyksi.

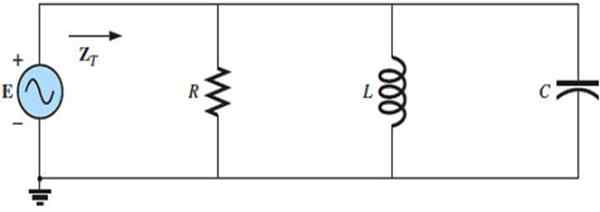RLC -piiri rinnakkain kytkettynä vuorottelevaan virran lähteeseen. Lähde: f. Zapata.

Liikuntaa

Edellisen osan sarjan 1 LRC -piirissä vastus on 200 ohmin arvoinen, induktanssi 0.4 tuntia ja lauhdutin on 6 μF. Virtalähde on puolestaan ​​vaihtoehtoinen amplitudjännite, joka on 30 V, usein 250 rad/s. Sitä pyydetään löytämään:

a) kunkin elementin reaktanssit

b) piirin impedanssimoduulin arvo.

c) virran amplitudi

Liittää jhk

Vastaavat reaktiot lasketaan kaavoilla:

XC = 1/ωc = 1/(250 rad/s x 6 x10-6 F) = 666,67 ohmia

XLens = Ωl = 250 rad/s x 0.4 h = 100 ohmia

Ja vastusreaktanssi vastaa sen arvoa ohmissa:

XR - = R = 200 ohmia

Ratkaisu b

Impedanssi Z määritellään syynä jännitteen ja piirin virran välillä joko sarjassa tai rinnakkain:

Z = vm / Yom

Impedanssi mitataan ohmina, samoin kuin vastus tai reaktanssi, mutta viittaa induktanssien ja kondensaatioiden virran kulkeutumiseen, kun otetaan huomioon, että niiden erityisten vaikutusten, kuten jännitteen viivästyminen tai eteneminen, lisäksi myös olla tietty sisäinen vastus.

Voidaan osoittaa, että RLC -sarjan piirissä impedanssimoduuli annetaan:

Kun arvioidaan lauseessa annettuja arvoja, se saadaan:

Liuos C

:

Z = vm / Yom

Sen on;

Yllyttääm = Vm / Z = 30 V / 601 ohmia = 0.05 a.

Kiinnostavia teemoja

Erot vuorotellen ja tasavirran välillä

Viitteet

  1. Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. MC Graw Hill.
  2. Boylestad, r. 2011. Johdanto piirianalyysiin.Toinen. Painos. Pearson.
  3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 6. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
  4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
  5. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.