Kuinka saada kolmion kulma? (Esimerkki)

On olemassa monia tapoja Laske kolmion sivut ja kulmat. Nämä riippuvat siitä kolmiotyypistä, jonka kanssa työskentelet.

Tässä yhteydessä näytetään, kuinka laskea oikean kolmion sivut ja kulmat olettaen, että tietyt kolmiotiedot tuttavien tuttavien kanssa.

Käytettävät elementit ovat:

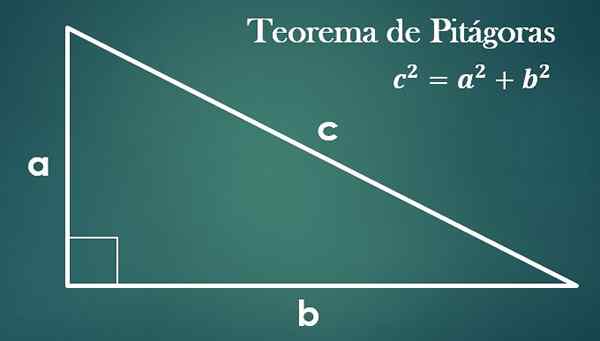
- Pythagoras -lause

Kun otetaan huomioon suorakulmio kolmio "A", "B" ja hypotenusa "C", on totta, että "c² = a²+b²".

- Kolmion alue

Kaava minkä tahansa kolmion alueen laskemiseksi on a = (b × h)/2, missä "B" on pohjan pituus ja "H" korkeuden pituus.

- Kolmion kulmat

Kolmion kolmen sisäkulman summa on 180 °.

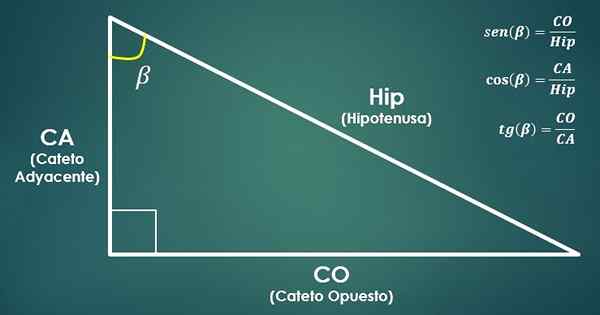
- Trigonometriset toiminnot:

Harkitse oikeaa kolmiota. Sitten trigonometriset funktiot määritetään beetakulman (β) sinus, kosiini ja tangentti seuraavasti:

sin (β) = co/hyp, cos (β) = ca/lonkka ja tan (β) = co/ca.

Kuinka laskea oikean kolmion sivut ja kulmat?

Annetaan ABC suorakulmio kolmio, seuraavat tilanteet voidaan esittää:

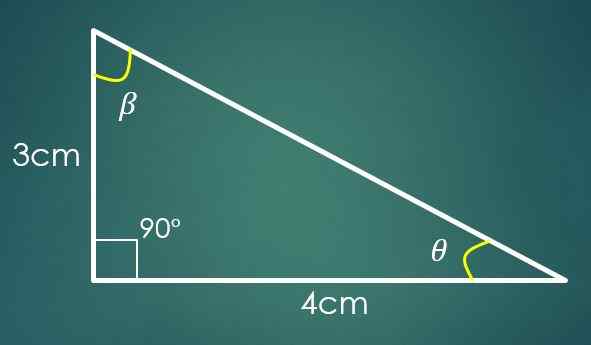
1- Kaksi jalkaa tunnetaan

Jos Cateto "A" mittaa 3 cm ja Cateto "B" mittaa 4 cm, niin "C" -arvon laskemiseksi käytetään Pythagoras -lausetta. Korvaamalla "A" ja "B" -arvot saadaan, että c² = 25 cm², mikä tarkoittaa, että c = 5 cm.

Nyt, jos kulma β on vastapäätä "B" -luokkaa, niin sin (β) = 4/5. Kun sovelletaan rinnan käänteistä toimintaa, tässä viimeisessä tasa -arvossa saadaan, että β = 53,13º. Kolmion kaksi sisäkulmaa on jo tiedossa.

Olkoon θ kulma, joka on vielä tiedossa, sitten 90º+53,13º+θ = 180 °, missä saadaan, että θ = 36,87º.

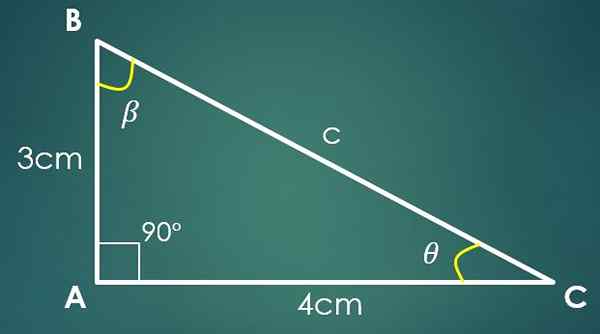
Tässä tapauksessa ei ole välttämätöntä, että tunnetut puolet ovat kaksi jalkaa, tärkeätä on tietää minkä tahansa kahden puolen arvo.

2- jalka ja alue tunnetaan

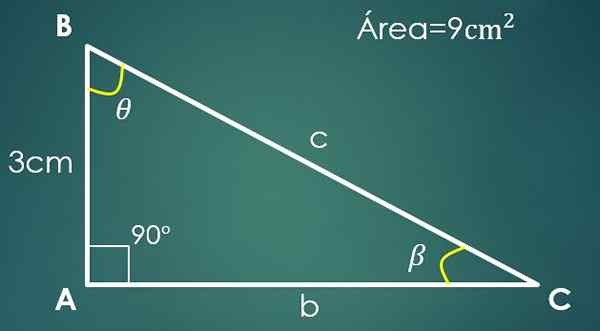
Olkoon A = 3 cm tunnettu jalka ja 9 cm² kolmioalue.

Suorakulmiokolmiossa luokkaa voidaan pitää pohjana ja toisena korkeutena (koska ne ovat kohtisuoria).

Oletetaan, että "A" on pohja, joten 9 = (3 × H)/2, missä saadaan, että toinen luokka mittaa 6 cm. Hypotenuksen laskemiseksi, jatka kuten edellisessä tapauksessa, ja on saatu, että c = √45 cm.

Nyt, jos kulma β on vastapäätä kuin “A” Catoto, niin synti (β) = 3/√45. Pel puhdistamisessa saadaan, että sen arvo on 26,57º. Sinun on vain tiedettävä kolmannen kulman arvo θ.

On täytetty, että 90 °+26,57º+θ = 180 °, missä päätelty, että θ = 63,43º.

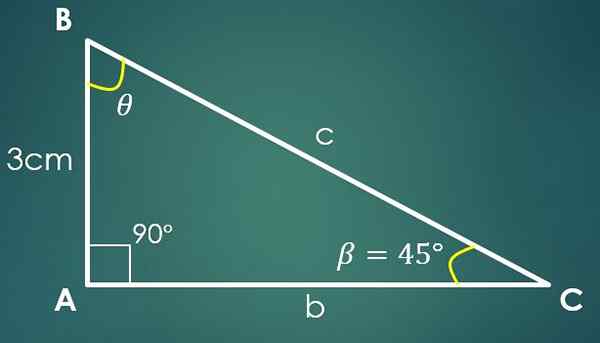
3- Kulma ja kateto tunnetaan

Olkoon β = 45 ° tunnettu kulma ja a = 3 cm tunnettu jalka, jossa kateto “A” on vastakkainen kulmaa β. Käyttämällä tangenttikaavaa, saadaan, että TG (45 °) = 3/ca, missä käy ilmi, että CA = 3 cm.

Käyttämällä Pythagoras -lausetta, saadaan, että c² = 18 cm², ts. C = 3√2 cm.

On tiedossa, että kulma mittaa 90 ° ja että β on 45 °, tästä lähtien on päätelty, että kolmas kulma mittaa 45 °.

Tässä tapauksessa tunnetun puolen ei tarvitse olla jalka, se voi olla mikä tahansa kolmion kolmesta puolesta.