Käsitteelliset kerroin käsite, kaava, laskenta, esimerkki

Hän palautuskerroin Se on osamäärä suhteellisen ylinopeuden nopeuden ja lähestymisen suhteellisen nopeuden välillä, jotka törmäävät kahteen kappaleeseen. Kun ruumiit yhdistyvät törmäyksen jälkeen, tämä osuus on mitätön. Ja yksikkö on arvoinen, jos törmäys on täysin joustava.

Oletetaan kaksi kiinteää massapalloa M1 ja massa M2 vastaavasti, että he kärsivät törmäyksestä. Juuri ennen törmäystä palloilla oli nopeuksia V1 ja V2 Tietyn inertiaalisen referenssijärjestelmän suhteen. Heti törmäyksen jälkeen niiden nopeudet muuttuvat V1 ' ja V2 '.

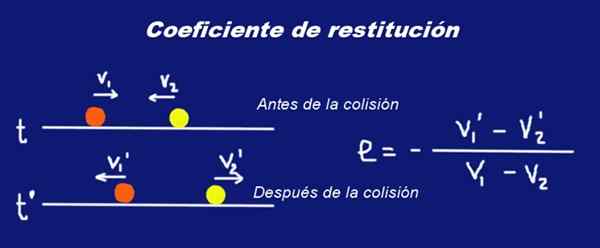Kuvio 1. Kahden massan M1 ja M2 ja niiden palautuskertoimen ja. Valmistaja: Ricardo Pérez.

Kirje on sijoitettu lihavoitu kirjasin Nopeudella osoittaa, että ne ovat vektorimääriä.

Kokeet osoittavat, että jokainen törmäys täyttää seuraavan suhteen:

V1 ' - V2 '= -ja (V1 - V2)

Missä ja Se on todellinen luku välillä 0 ja 1, nimeltään palautuskerroin törmäys. Edellinen ilmaus tulkitaan seuraavasti: 

Kahden hiukkasen suhteellinen nopeus ennen törmäystä on verrannollinen kahden hiukkasen suhteelliseen nopeuteen törmäyksen jälkeen, suhteellisuusvakio on (-e), missä E on törmäyksen palautuskerroin.

[TOC]

Mikä on palautuskerroin?

Tämän kertoimen hyödyllisyys on joustamattomuuden aste törmäys. Jos törmäys on täysin joustava, kerroin on 1, kun taas täysin joustavassa törmäyksessä kerroin on 0, koska tässä tapauksessa suhteellinen nopeus törmäyksen jälkeen on nolla.

Vastavuoroisesti, jos törmäyksen palautuskerroin ja hiukkasten nopeudet tunnetaan ennen sitä, niin nopeudet voidaan ennustaa tällaisen törmäyksen jälkeen. 

Voi palvella sinua: 13 esimerkkiä Newtonin ensimmäisestä laista tosielämässä

Vauhti

Törmäyksissä palautuskertoimen luoman suhteen lisäksi on toinen perussuhde, joka on Vauhtia.

Vauhti p hiukkasen tai liikkeen määrän, kuten sitä kutsutaan myös, se on massan tuote M hiukkasen nopeus V. Eli: vauhti p Se on vektorisäki.

Törmäyksissä lineaarinen vauhti P Järjestelmä on sama juuri ennen törmäyksen jälkeen, koska ulkovoimat ovat halveksittavia lyhyitä, mutta voimakkaita sisäisen vuorovaikutuksen voimia törmäyksen aikana. Mutta vauhdin säilyttäminen ei riitä P järjestelmän ratkaisemiseksi törmäyksen yleisen ongelman ratkaisemiseksi.

Aiemmin mainitussa tapauksessa kahden M1- ja M2 -pallot, jotka törmäävät, lineaarisen vauhdin säilyttäminen on kirjoitettu näin:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Törmäysongelmaa ei voida ratkaista, jos palautuskerrointa ei tunneta. Momentin säilyttäminen, vaikka se on välttämätöntä, ei ole riittävä ennustamaan nopeuksia törmäyksen jälkeen.

Kun ongelmassa todetaan, että ruumiit liikkuvat yhdessä törmäyksen jälkeen, epäsuorasti sanoo, että palautuskerroin on 0.

Kuva 2. Biljardipalloissa on palautuskertoimen törmäyksiä vähän vähemmän kuin 1. Lähde: Pixabay.

Energia- ja korvauskerroin 

Toinen tärkeä fyysinen määrä törmäyksiin on energia. Törmäyksien aikana on olemassa vaihtoja kineettisen energian, potentiaalienergian ja muun tyyppisen energian, kuten kalorienergian, vaihtoon.

Ennen törmäystä ja sen jälkeen vuorovaikutuksen potentiaalinen energia on käytännössä nolla, joten energiatasapaino sisältää hiukkasten kineettisen energian ennen ja jälkeen ja määrän Q - kutsutaan hävitetyksi energiaksi.

Se voi palvella sinua: Heisenberg Atomic -malli

Kahdelle M1- ja M2 -massapalloille, jotka törmäävät energiatasapainoon ennen törmäystä ja sen jälkeen, se on kirjoitettu näin:

½ m1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + Q

Kun vuorovaikutusvoimat törmäyksen aikana ovat puhtaasti konservatiivisia, tapahtuu Kokonaistenergia Sitä törmäävistä hiukkasista, ts. Se on sama ennen törmäystä ja sen jälkeen (Q = 0). Kun näin tapahtuu, sanotaan, että törmäys on täysin joustava.

Joustavien törmäysten tapauksissa energiaa ei hävitetä. Ja myös palautuskerroin noudattaa: E = 1. 

Päinvastoin, joustamattomissa törmäyksissä, jotka ≠ 0 ja 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Jotta törmäysongelma voidaan määrittää täydellisesti, on tarpeen tuntea palautuskerroin tai vuorotellen törmäyksen aikana hajoavan energian määrä.

Palautuskerroin riippuu kahden ruumiin välisen vuorovaikutuksen luonteesta ja tyypistä törmäyksen aikana.

Toisaalta kehon suhteellinen nopeus ennen törmäystä määrittelee vuorovaikutuksen voimakkuuden ja siten sen vaikutuksen palautuskertoimeen. 

Kuinka palautuskerroin lasketaan?

Havainnollistaaksemme, kuinka törmäyksen palautuskerroin lasketaan, otamme yksinkertaisen tapauksen:

Oletetaan, että kahden massan pallot törmäävät M1 = 1 kg ja M2 = 2 kg jotka liikkuvat suorassa kitkassa (kuten kuvassa 1).

Ensimmäinen pallo vaikuttaa alkuperäiseen nopeuteen V1 = 1 m/s Noin toisesta, joka on alun perin levossa, se on V2 = 0 m/s.

Se voi palvella sinua: Termodynamiikan ensimmäinen laki: kaavat, yhtälöt, esimerkit

Heidän törmäyksen jälkeen he liikkuvat näin: ensimmäinen pysähtyy (V1 '= 0 m/s) ja toinen siirtyy oikealle nopeudella V2 '= 1/2 m/s.

Palautuskertoimen laskemiseksi tässä törmäyksessä käytämme suhdetta:

V1 ' - V2 ' = -ja ( V1 - V2 -A 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Esimerkki

Edellisen jakson kahden alueen yhden dimensionaalisessa törmäyksessä laskettiin sen palautuskerroin, mikä johtaa E = ½ .

Kuten e ≠ 1, törmäys ei ole joustava, ts. Järjestelmän kineettinen energia ei säilytetä, ja siellä on jonkin verran hajoavaa energiaa Q (esimerkiksi pallojen lämmitys törmäyksen takia).

Määritä Joulesissa hävitetyn energian arvo. Laske myös hajotetun energian prosenttiosuus.

Ratkaisu

Pallon 1 alkuperäinen kineettinen energia on: 

K1i = ½ M1 V1^2 = ½ 1 kg (1 m/s)^2 = ½ J

Kun taas pallo 2 on nolla, koska se on alun perin levossa.

Joten järjestelmän alkuperäinen kineettinen energia on Ki = ½ J.

Kun törmäyksen jälkeen vain toinen pallo liikkuu nopeudella v2 '= ½ m/s, joten järjestelmän lopullinen kineettinen energia on:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ J

Eli törmäyksessä hajotettu energia on:

Q = Ki - kf = (½ J - ¼ J) = 1/4 J

Ja tässä törmäyksessä hajoavan energian osuus lasketaan seuraavasti:

F = q / ki = ¼ / ½ = 0,5, toisin sanoen, että 50% järjestelmän energiasta on hävitetty joustamattoman törmäyksen takia, jonka palautuskerroin on 0,5.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
3. Ritari, r. 2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Wikipedia. Liikkeen määrä.Palautettu: on.Wikipedia.org.